Proporção - propriedades e exercícios resolvidos

Artigo sobre Propriedades das proporções com exemplos resolvidos.

Proporção

é a igualdade entre duas razões. A proporção entre A/B e C/D é a igualdade:

A/B=C/D

Propriedades das proporções

Propriedade 1: Qualquer que seja a proporção, o produto dos extremos é igual ao produto dos meios. 

Propriedade 2: Qualquer que seja a proporção, a soma ou a diferença dos antecedentes está para a soma ou a diferença dos consequentes, assim como cada antecedente está para o seu respectivo consequente. Temos então:

     ou     

Ou

     ou     

Propriedade 3: Qualquer que seja a proporção, a soma ou a diferença dos dois primeiros termos está para o primeiro, ou para o segundo termo, assim como a soma ou a diferença dos dois últimos termos está para o terceiro, ou para o quarto termo. Então temos:

     ou     

Ou

     ou     

Quarta proporcional
Dados três números a, b, e c, chamamos de quarta proporcional o quarto número x que junto a eles formam a proporção:

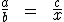Tendo o valor dos números a, b, e c, podemos obter o valor da quarta proporcional, o número x, recorrendo à propriedade fundamental das proporções. O mesmo procedimento utilizado na resolução de problemas de regra de três simples.

Terceira proporcional

Em uma proporção onde os meios são iguais, um dos extremos é a terceira proporcional do outro extremo:

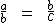Na proporção acima a é a terceira proporcional de c e vice-versa.

Fontes: www.matematicadidatica.com.br/    www.mundoeducacao.com/

       

Exercícios resolvidos

1) A soma de dois números é igual a 240. Sabe-se que um deles está para 5, assim como o outro está para 7. Quais são estes números?

Resolução - questão 01

Para a resolução deste exemplo utilizaremos a quinta propriedade das proporções. Chamando um dos números de a e o outro de b, podemos montar a seguinte proporção:

Sabemos que a soma de a com b resulta em 240, assim como a adição de 5 a 7 resulta em 12. Substituindo estes valores na proporção teremos:

Portanto:

Concluímos então que os dois números são 100 e 140.

---

2) (UERE1102/070-AssistAdministrativoII - 2012) – Segundo uma reportagem, a razão entre o número total de alunos matriculados em um curso e o número de alunos não concluintes desse curso, nessa ordem, é de 9 para 7. A reportagem ainda indica que são 140 os alunos concluintes desse curso. Com base na reportagem, pode-se afirmar, corretamente, que o número total de alunos matriculados nesse curso é

(A) 180.
(B) 260.
(C) 490.
(D) 520.
(E) 630.

3) (VNSP1214/001-AssistenteAdministrativo-I – 2012) – Em uma padaria, a razão entre o número de pessoas que tomam café puro e o número de pessoas que tomam café com leite, de manhã, é 2/3. Se durante uma semana, 180 pessoas tomarem café de manhã nessa padaria, e supondo que essa razão permaneça a mesma, pode-se concluir que o número de pessoas que tomarão café puro será:

(A) 72.

(B) 86.

(C) 94.

(D) 105.

(E) 112.

4) Quatro números, todos diferentes de zero, 10, 8, 25 e x formam nesta ordem uma proporção. Qual o valor de x?

Resolução - Questão 04

Seguindo o explicado na propriedade 1 temos:

O valor do número x é 20.

_______________________________________________________________________

5) Calcule o valor da seguinte proporção:

 

6 * (x + 1) = 2 * 18
6x + 6 = 36
6x = 36 – 6
6x = 30
x = 30/6
x = 5

________________________________________________________________________

6) Dois números a e b diferem entre si em 18 unidades. a está para b, assim como 825 está para 627. Qual o valor de a e de b?

Resolução - Questão 06

Da segunda propriedade das proporções temos:

Sabemos que a diferença entre a e b resulta em 18, assim como 825 menos 627 resulta em 198. Substituindo tais valores na proporção temos:

Para calcularmos o valor de a temos:

Portanto:

75 e 57 respectivamente se referem ao valor de a e de b

7) (FAPE1201/001-AnalistaAdministrativo – 2012) – Em uma fundação, verificou-se que a razão entre o número de atendimentos a usuários internos e o número de atendimento total aos usuários (internos e externos), em um determinado dia, nessa ordem, foi de . Sabendo que o número de usuários externos atendidos foi 140, pode-se concluir que, no total, o número de usuários atendidos foi

(A) 84.
(B) 100.
(C) 217.
(D) 280.
(E) 350.

8) (SPTR1101/009-TécnicoInformática – 2012) – Em uma concessionária de veículos, a razão entre o número de carros vermelhos e o número de carros prateados vendidos durante uma semana foi de 3/11. Sabendo-se que nessa semana o número de carros vendidos (somente vermelhos e prateados) foi 168, pode-se concluir que, nessa venda, o número de carros prateados superou o número de carros vermelhos em

(A) 96.
(B) 112.
(C) 123.
(D) 132.
(E) 138.



9) Sabendo-se que x-y=18, determine x e y na proporção .
Resolução - Questão 09

• Solução:

            Pela propriedade 3 temos que:

          

  

           

            x-y = 18   =>   x=18+y   =>   x = 18+12    =>   x=30.
            Logo, x=30 e y=12.

10) Relativamente aos tempos de serviço de dois funcionários do Banco do Brasil, sabe-se que sua soma é 5 anos e 10 meses e que estão entre si na razão 3/2.
Nessas condições,  a diferença positiva entre os tempos de serviço desses funcionários é de:

a) 2 anos e 8 meses
b) 2 anos e 6 meses
c) 2 anos e 3 meses
d) 1 ano e 5 meses
e) 1 ano e 2 meses

Resolução - Questão 10

5 anos e 10 meses = (5*12 + 10) meses = 70 meses

x + y = 70

x/y = 3/2

x = 3y/2

3y/2 + y = 70

3y + 2y = 140

y = 140/5

y = 28

x = 70 - 28

x = 42

Diferença positiva = 42 - 28 = 14

A diferença é de 1 ano e 2 meses <==== RESPOSTA Letra E.

11) A soma de dois números é igual a 240. Sabe-se que um deles está para 5, assim como o outro está para 7. Quais são estes números?

Resolução - Questão 11

Para a resolução deste exemplo utilizaremos a segunda propriedade das proporções. Chamando um dos números de a e o outro de b, podemos montar a seguinte proporção:

Sabemos que a soma de a com b resulta em 240, assim como a adição de 5 a 7 resulta em 12. Substituindo estes valores na proporção teremos:

Portanto:

Concluímos então que os dois números são 100 e 140.

12) Quatro números, todos diferentes de zero, 10, 8, 25 e x formam nesta ordem uma proporção. Qual o valor de x?

Resolução - Questão 12

Seguindo o explicado sobre a quarta proporcional temos:

O valor do número x é 20.

13) Para cada 2 automóveis que vende, Carlos ganha R$ 200,00 de comissão. Quanto ele recebeu de comissão no mês que vendeu 15 automóveis? 

Resolução - Questão 13

2x = 3000
x = 3000 / 2
x = 1500

Carlos recebeu R$ 1.500,00 de comissão pela venda de 15 automóveis.


14) Um relógio atrasa 5 minutos a cada 8 horas. Quanto tempo ele atrasará em 4 dias? 

Resolução - Questão 14

8 horas = 8 * 60 minutos = 480 minutos 
4 dias = 4 * 24 = 96 horas = 5760 minutos 



480x = 28800 
x = 28800 / 480 
x = 60 minutos 

Portanto, o relógio atrasará 60 minutos, ou seja, 1 hora. 

15) (SEED0802/01-AgOrgEscolar – 2009) – Paulo acertou 75 questões da prova objetiva do último simulado. Sabendo-se que a razão entre o número de questões que Paulo acertou e o número de questões que ele respondeu de forma incorreta é de 15 para 2, e que 5 questões não foram respondidas por falta de tempo, pode-se afirmar que o número total de questões desse teste era

(A) 110.

(B) 105.

(C) 100.

(D) 95.

(E) 90.

16)  (CORM1001/07-AssistTécAdm-OpTel – 2011) – Em uma sala de aula, a razão entre meninos e meninas é de 3 para 7, nesta ordem. Em agosto, entraram mais 3 meninos nessa sala, mas uma menina mudou de colégio e isso fez com que a razão entre meninos e meninas agora fosse de 3 para 5. O número total de alunos dessa sala, em agosto, após essas mudanças, passou a ser de

(A) 28.

(B) 30.

(C) 32.

(D) 34.

(E) 38.

17) Três pessoas formaram uma sociedade, A entrou com R$ 24.000,00; B com R$ 30.000,00 e C com R$ 36.000,00. Depois de três meses tiveram um lucro de R$ 60.000,00. Calcule o lucro de cada  sócio.

Resolução - Questão 17: 

Para cada sócio, a razão entre o lucro e o dinheiro investido é igual a razão entre o lucro total da sociedade e o total investido pela sociedade. Então, temos a proporção:

Assim, A/24000 = B/30000 = C/36000 = 2/3.  
Logo:  A = R$ 24.000,00 × 2/3 = R$ 16.000,00 ;  B = R$ 30.000,00 × 2/3 = R$ 20.000,00 ;  C = R$ 36.000,00 × 2/3 = R$ 24.000,00.

18) O peso de uma sacola em kg está para o peso de uma outra sacola também em kg, assim como 32 está para 28. Quanto pesa cada uma das sacolas, sabendo-se que juntas elas pesam 15kg?

Resolução - Questão 18: 

Identifiquemos o peso da primeira sacola por a e o peso da segunda por b. Como expresso no enunciado, temos que a está para b, assim como 32 está para 28. Da segunda propriedade das proporções temos que:

Temos que a e b somados resultam em 15, assim como 32 mais 28 resulta em60. Substituindo-os na proporção temos:

Calculemos o valor de b:

Portanto:

Uma das sacolas pesa 8kg ao passo que a outra pesa 7kg.

19) Dois números a e b diferem entre si em 18 unidades. a está para b, assim como 825 está para 627. Qual o valor de a e de b?

Resolução - Questão 19: 

Da segunda propriedade das proporções temos:

Sabemos que a diferença entre a e b resulta em 18, assim como 825 menos 627 resulta em 198. Substituindo tais valores na proporção temos:

Para calcularmos o valor de a temos:

Portanto:

75 e 57 respectivamente se referem ao valor de a e de b.

Fonte: www.profjosimar.com.br/

           www.matematicadidatica.com.br

DATAHOSTING.COM.BR|DE http://www.datahosting.com.br/afiliados/ok.php?id=8893

HOSPEDAGEM DE SITES R$14,90 com 10GB de Espaço e 150GB de Tráfego, Construtor de Sites e...

Hospedagem de sites com planos gigantes a partir de R$14,90, 10GB de espaço, 150Gb de tráfego de

DATAHOSTING.COM.BR|DE WWW.DATAHOSTING.COM.BR