Artigo com questões resolvidas de vestibulares sobre cinemática e principais fórmulas
Principais fórmulas da cinemática - física
Movimento Uniforme (MU)
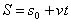 Velocidade escalar média
Velocidade escalar média
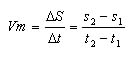
Movimento Uniformemente Variado (MUV)
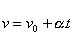
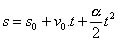
Equação de Torricelli (MUV)
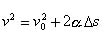
Aceleração escalar instantânea
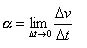
Aceleração escalar
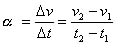
Movimento circular uniforme (MCU)
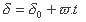
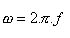
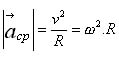
Movimento circular uniformemente variado (MCUV)
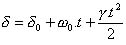
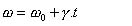
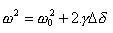
considerando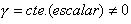
aceleração: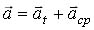
onde a aceleração tangencial =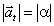
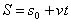 Velocidade escalar média
Velocidade escalar média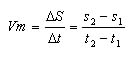
Movimento Uniformemente Variado (MUV)
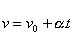
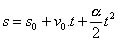
Equação de Torricelli (MUV)
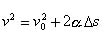
Aceleração escalar instantânea
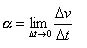
Aceleração escalar
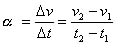
Movimento circular uniforme (MCU)
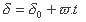
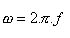
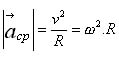
Movimento circular uniformemente variado (MCUV)
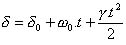
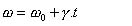
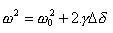
considerando
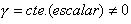
aceleração:
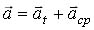
onde a aceleração tangencial =
Questões resolvidas de vestibulares de Cinemática
1) Em um trecho de declive de 10km, a velocidade máxima permitida é de 70km/h. Suponha que um carro inicie este trecho com velocidade igual a máxima permitida, ao mesmo tempo em que uma bicicleta o faz com velocidade igual a 30km/h. Qual a distância entre o carro e a bicicleta quando o carro completar o trajeto?
- Carro:
S=10km
v=70km/h
t=?
S=70t
10=70t
0,14h=t
t=8,57min (usando regra de três simples)
- Bicicleta
O tempo usado para o cálculo da distância alcançada pela bicicleta, é o tempo em que o carro chegou ao final do trajeto: t=0,14h
v=30km/h
t=0,14h
S=?
S=0+30.(0,14)
S=4,28Km
2) Dois trens partem simultaneamente de um mesmo local e percorrem a mesma trajetória retilínea com velocidades, respectivamente, iguais a 300km/h e 250km/h. Há comunicação entre os dois trens se a distância entre eles não ultrapassar 10km. Depois de quanto tempo após a saída os trens perderão a comunicação via rádio?
Para este cálculo estabelece-se a velocidade relativa entre os trens, assim pode-se calcular o movimento como se o trem mais rápido estivesse se movendo com velocidade igual a 50km/h (300km/h-250km/h) e o outro parado.
Assim:
v=50km/h
S=10km
t=?
3) Um carro, se desloca a uma velocidade de 20m/s em um primeiro momento, logo após passa a se deslocar com velocidade igual a 40m/s, assim como mostra o gráfico abaixo. Qual foi o distância percorrida pelo carro?
Tendo o gráfico da v x t, o deslocamento é igual à área sob a reta da velocidade. Então:
S= Área A + Área B
S=20 5 + 40
5 + 40 (15-5)
(15-5)
S=100+400
S=500m
4) Um carro viaja de uma cidade A a uma cidade B, distantes 200km. Seu percurso demora 4 horas, pois decorrida uma hora de viagem, o pneu dianteiro esquerdo furou e precisou ser trocado, levando 1 hora e 20 minutos do tempo total gasto. Qual foi a velocidade média que o carro desenvolveu durante a viagem?
S=200km
t=4h
v=?
Mesmo o carro tendo ficado parado algum tempo durante a viagem, para o cálculo da velocidade média não levamos isso em consideração.
5) No exercício anterior, qual foi a velocidade nos intervalos antes e depois de o pneu furar? Sabendo que o incidente ocorreu quando faltavam 115 km para chegar à cidade B.
- Antes da parada:
S= 200-115=85km
t=1hora
v=?
- Depois da parada:
S= 115km
t= 4h-1h-1h20min= 1h40min=1,66h (utilizando-se regra de três simples)
v=?
6) Um carro desloca-se em uma trajetória retilínea descrita pela função S=20+5t (no SI). Determine:
(a) a posição inicial;
(b) a velocidade;
(c) a posição no instante 4s;
(d) o espaço percorrido após 8s;
(e) o instante em que o carro passa pela posição 80m;
(f) o instante em que o carro passa pela posição 20m.
Comparando com a função padrão: 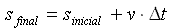
(a) Posição inicial= 20m
(b) Velocidade= 5m/s
(c) S= 20+5t
S= 20+5.4
S= 40m
(d) S= 20+5.8
S= 60m
(e) 80= 20+5t
80-20=5t
60=5t
12s =t
(f) 20= 20+5t
20-20= 5t
t=0
7) Um automóvel encontra-se parado diante de um semáforo. Logo quando o sinal abre, ele arranca com aceleração 5m/s², enquanto isso, um caminhão passa por ele com velocidade constante igual a 10m/s.
(a) Depois de quanto tempo o carro alcança o caminhão?
(b) Qual a distância percorrida até o encontro.
Escreve-se as equações do muv para o carro e do mu para o caminhão:
Carro:
Caminhão:
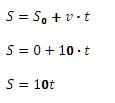
Quando os dois se encontram, suas posições são iguais, então:
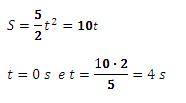
(b) Sabendo o momento do encontro, só é necessário aplicá-lo em uma das duas funções (do caminhão ou do carro).
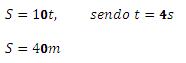
Logo o carro encontra o caminhão 4 segundos após a sinaleira abrir, a uma distância de 40 m.
8) Uma pedra é abandonada de um penhasco de 100m de altura. Com que velocidade ela chega ao solo? Quanto tempo demora para chegar?
9) Durante a gravação de um filme, um dublê deve cair de um penhasco de 30m de altura e cair sobre um colchão. Quando ele chega ao colchão, este sofre uma deformação de 1m. Qual é a desaceleração que o dublê sofre até parar quando chega colchão?
A desaceleração sofrida pelo dublê se dará quando a velocidade inicial for a velocidade de chegada ao solo na queda vertical, a velocidade final for zero, e a distância do deslocamento for 1m de deformação do colchão. Então o primeiro passo para chegar a resolução é descobrir a velocidade de chegada ao solo:
Como no exercício não é dado o tempo, a maneira mais rápida de se calcular a velocidade é através da Equação de Torricelli para o movimento vertical, com aceleração da gravidade positiva, já que o movimento é no mesmo sentido da gravidade.
O segundo passo é calcular o movimento uniformemente variado para a desaceleração da queda. Com velocidade inicial igual a 24,5m/s.
10) Um fazendeiro precisa saber a profundidade de um poço em suas terras. Então, ele abandona uma pedra na boca do poço e cronometra o tempo que leva para ouvir o som da pedra no fundo. Ele observa que o tempo cronometrado é 5 segundos. Qual a altura do poço?
Podemos dividir o movimento em movimento da pedra e o deslocamento do som.
- Movimento da Pedra:
- Deslocamento do som:
Sabendo que a altura do poço é a mesma para as duas funções e que 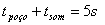 :
:
mas 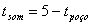 , então:
, então:
Sabendo que 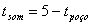
Tendo os tempos de cada movimento, podemos calcular a altura utilizando qualquer uma das duas funções:
11) Uma motocicleta se desloca com velocidade constante igual a 30m/s. Quando o motociclista vê uma pessoa atravessar a rua freia a moto até parar. Sabendo que a aceleração máxima para frear a moto tem valor absoluto igual a 8m/s², e que a pessoa se encontra 50m distante da motocicleta. O motociclista conseguirá frear totalmente a motocicleta antes de alcançar a pessoa?
Como a aceleração utilizada para frear a moto se opõe ao movimento, tem valor negativo, então:
A motocicleta não irá parar antes de atingir a pessoa.
12) Um tiro de canhão é lançado formando um ângulo de 30° com a horizontal, conforme a figura abaixo:
Então a altura que o tiro do canhão alcança é igual a 50m+30m=80m
13) Suponha que você precise jogar um livro, do segundo andar de um prédio, para um amigo que esteja a 10m de distância de você. Qual deve ser a velocidade inicial com que você deverá lançá-lo? Sabendo que você vai realizar o lançamento verticalmente e que a janela de um segundo andar está a 4 metros de altura do chão.
14) Se considerarmos um relógio, no exercício anterior, com ponteiro das horas de 10cm, dos minutos de 15cm e dos segundos de 20cm. Qual será a aceleração centrípeta de cada um dos ponteiros?
O primeiro passo para a resolução é transformar a velocidade linear pedida em velocidade angular
(b) 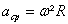
(c) 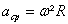
15) Uma roda de 1 metro de diâmetro, partindo do repouso começa a virar com aceleração angular igual a 2rad/s². Quanto tempo ele demora para atingir uma velocidade linear de 20m/s?
O primeiro passo para a resolução é transformar a velocidade linear pedida em velocidade angular, considerando que o raio da roda é igual a metade do diâmetro. Então:
A partir daí, apenas se aplica a função horária da velocidade angular:
16) Uma bola de bilhar, com raio igual a 2,5cm, após ser acertada pelo jogador, começa a girar com velocidade angular igual a 5rad/s, e sofre uma desaceleração igual a -1rad/s² até parar, qual o espaço percorrido pela bola?
17) Os ponteiros do relógio realizam um movimento circular uniforme. Qual a velocidade angular dos ponteiros (a) das horas, (b) dos minutos (c) e dos segundos?
(a) O ponteiro das horas completa uma volta (2π) em 12 horas (12∙3600s)
ωh=∆φt
ωh=2π12∙3600=1,45∙10-4 rad/s
(b) O ponteiro dos minutos completa um volta (2π) em uma hora (3600s)
ωm=∆φt
ωm=2π3600=1,74∙10-3 rad/s
(c) O ponteiro dos segundos completa uma volta (2π) em um minuto (60s)
ωs=∆φt
ωs=2π60=0,105 rad/s
18) (UFPR) Um modelo de foguete disparado verticalmente do chão se eleva com aceleração vertical constante de 2,0 m/s² por 8,0 s. Seu combustível então se esgota e ele continua se deslocando para cima em “queda livre”, isto e, apenas sob a ação da gravidade, e depois volta caindo.
(a) Qual a altitude máxima alcançada?
(b) Qual o tempo total decorrido da decolagem ate o foguete bater no chão?
Resolução
(a) Adotaremos a origem do eixo vertical y, que aponta pra cima, como sendo o nível do chão. Começaremos a contar o tempo a partir do lançamento, quando o foguete esta em repouso. O movimento ocorre em duas etapas distintas.
Nos primeiros 8 s, o foguete e acelerado pra cima com aceleração a1 = 2 m/s², a partir do repouso, v (1)
No final destes 8 s, a velocidade do foguete e

Neste instante tf também podemos calcular a posição do foguete:

Depois disso, o foguete entra em outro regime de movimento, e voltamos a zerar o cronometro. Ele esta inicialmente a uma velocidade v (2) i = v (1) f , e passa a ser desacelerado pela gravidade, de modo que o instante τ, para o qual a ele atinge a altura máxima, e dado por

Nesse instante, nesta segunda etapa, sabendo que a posição inicial e y (2) vale

Esta foi a altura máxima alcançada.
(b) Na segunda etapa, o instante τc em que o foguete retorna ao chão e dado por

ig τc − 2y
O valor negativo para τc deve ser descartado. Somando este tempo aos 8 s da primeira etapa do movimento, o tempo total de voo vale 13,5 s.
19) (UFPR) Uma bola de futebol e chutada do chao com uma velocidade inicial de 70,2 km/h fazendo um angulo de 45,0o para cima. Naquele instante, o goleiro a uma distancia de 52,8 m na direcao do chute comeca a correr para receber a bola e consegue chegar a tempo de agarra-la no ar (sem saltar) a uma altura de 2,45 m simplesmente erguendo os bracos.
(a) Qual foi o tempo de voo da bola?
(b) Qual foi a velocidade escalar media desenvolvida pelo goleiro?
Resolução
(a) Considerando que, no momento do chute, a bola esteja na origem do eixo de coordenadas, a expressao geral para o movimento do projetil e dada por:

sendo


Supondo que a bola atingiu a altura yG = 2,45 m no instante τ, podemos escrever
sendo L a coordenada x da bola neste instante τ. Por outro lado, da equacao de movimento,

Igualando as componentes y:

Substituindo os valores:


O valor menor de τ refere-se ao instante em que a bola passou pela posicao yG, subindo. Procuramos o instante em que a bola esta em yG, so que descendo: τ = 2,57 s.
(b) Do enunciado, podemos dizer que a posicao inicial do goleiro e x (G) i = 52,8 m. Quando ele agarrou a bola, sua coordenada x era x (G) f = L, sendo que R e dado por


Portanto, como a distancia percorrida pelo goleiro e igual ao seu deslocamento

20) Um avião se move para o leste enquanto o piloto aproa o avião um pouco para o sul a partir do leste, contra um vento regular que sopra pra nordeste. O avião possui velocidade ~vAV em relação ao vento de 215 km/h, na direção sudeste fazendo um angulo θ com o leste. O vento possui velocidade ~vVC em relação ao chão, de modulo 65 km/h, na direção nordeste fazendo um angulo de 30◦ com o norte.
(a)Qual e o modulo da velocidade ~vAC do avião em relação ao chão?
(b) Qual e o valor de θ?
Resolução
Em primeiro lugar, vamos assumir que o eixo x aponta de oeste para leste, e o eixo y de sul para norte. Com relação ao chão, a velocidade do avião pode ser escrita como
Com relação a velocidade do avião com relação ao vento, podemos afirmar que:
com |~vAV | = 215 km/h. E a velocidade do vento com relação ao chão vale:
com |~vAV | = 215 km/h. Estas três velocidades se relacionam da seguinte maneira:

Comparando a ultima equação com a primeira, notamos que a coordenada y da ultima deve se anular:
Usando este valor na componente x,
21) Uma móvel parte da origem do eixo x com velocidade constante igual a 3m/s. No instante t=6s o móvel sofre uma aceleração a= -4m/s2. A equação horária, a partir do instante t=6s, será?
De t=0 até t=6s temos um MRU.
Logo a equação horária é:
A posição em t=6s será
Daí pra frente temos um MRUV:

22) Percorrendo-se uma distância "d" a 30km/h gasta-se 2 h menos do que se percorresse a 12km/h. Qual o valor de "d"?
1º caso:
d = 30.(t – 2)
2º caso
d = 12.t
Podemos igualar as duas expressões:
30.(t – 2) = 12t
Basta isolar “t” e substituir em uma das equações anteriores.
30t – 60 = 12t
30t – 12t = 60
18t = 60
t = 60/18 = 10/3h
30t – 12t = 60
18t = 60
t = 60/18 = 10/3h
Logo,
d = 12.t è d = 12 x 10/3 = 40km
23) Um móvel percorre a distância em linha reta entre duas cidades em duas etapas. Na primeira etapa ele percorre com uma rapidez 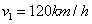 e na segunda etapa com uma rapidez
e na segunda etapa com uma rapidez 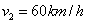 . Determine a rapidez média supondo que as duas etapas possuem o mesmo comprimento
. Determine a rapidez média supondo que as duas etapas possuem o mesmo comprimento
A rapidez média na viagem entre as duas cidades é dada por:
Pode-se afirmar que
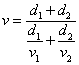 è
è
a)
Chamando de “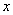 ” a distância em cada metade da viagem
” a distância em cada metade da viagem
então
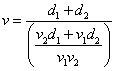 è
è 
 è
è 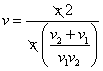
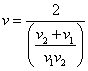 è
è 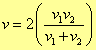
24) Dois amigos, correndo sobre uma mesma pista retilínea e em sentidos opostos, avistam-se quando a distância que os separa é de 150m. Um está correndo com velocidade escalar constante de 5,0 m/s e o outro com velocidade escalar constante de - 7,5 m/s. Que distância cada um percorrerá na pista, desde que se avistam até o instante em que um passa pelo outro?"

Para calcular o intervalo de tempo que eles levaram para se encontrar, podemos usar:
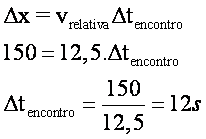
O deslocamento de cada um será:
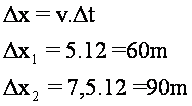
25) Um móvel A com movimento retilíneo uniforme parte de um ponto a em direção a b, com velocidade de 90 km/h. No mesmo instante sai de b um móvel B, também com MRU. A distância retilínea ab é de 10km. Calcule a velocidade do móvel B, para que ambos se cruzem a 6km de A.
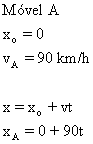
como o encontro deve ser em 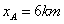 , teremos
, teremos
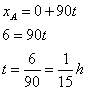
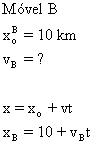 ,
,
substituindo  e
e 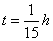 , teremos
, teremos
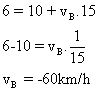
26) Dois moveis em MRU partem simultaneamente dos pontos A e B em sentidos contrários e se encontram pela primeira vez a 720m de A, a velocidade do que parte do ponto A é va e a velocidade do que parte do ponto B é vb. Cada móvel ao chegar ao ponto oposto ao da partida para por 10 minutos e retornam. O segundo ponto de encontro está situado a 400m do ponto B. Pede-se a distancia entre os pontos A e B.



Certamente os intervalos de tempo “t” necessários para cada encontro serão os mesmos.
Temos 4 equações
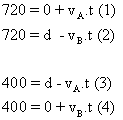
Basta resolver este sistema.
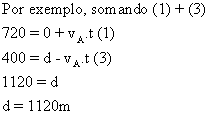
Testando:
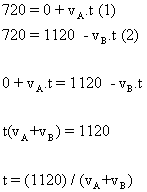
Substituindo
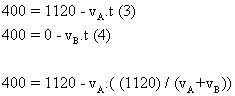
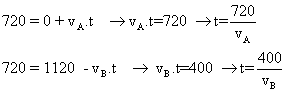
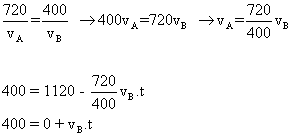
27) Determine a velocidade de um projétil disparado contra um alvo rotativo disposto a 15m de distância, sabendo-se que o alvo executa 300 revoluções por minuto e o arco medido entre o ponto visado no momento do disparo e o ponto de impacto do projétil no alvo é de 180º.
A freqüência do alvo é:
f = número de rotações / tempo
f = 300 / 60s = 5Hz
f = número de rotações / tempo
f = 300 / 60s = 5Hz
A distância percorrida pelo “ponto” é de:
delta x = delta phi . R
delta x = pi.R
delta x = pi.R
A velocidade linear do ponto é de:
v = delta x / delta t
v = delta x / delta t
ou
v = w.R
v = 2.pi.f.R
v = 2.pi.f.R
Igualando as duas:
delta x / delta t = 2.pi.f.R
pi.R / delta t = 2.pi.f.R
1 / delta t = 2.f
pi.R / delta t = 2.pi.f.R
1 / delta t = 2.f
delta t = 1 / 2f
delta t = 1 / 2.5 = 1/10 s
delta t = 1 / 2.5 = 1/10 s
A rapidez do projétil será:
v = delta x / delta t = 15m / (0,1s) = 150 m/
v = delta x / delta t = 15m / (0,1s) = 150 m/
28) Uma super mosca persegue um automóvel de comprimento 3 m. A velocidade da super mosca é o dobro da do automóvel. Calcular, em metros, o deslocamento da mosca, ao ultrapassar totalmente o automóvel.
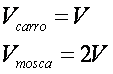
Nos problemas envolvendo ultrapassagens, use sempre:

Onde:
Temos então:
logo
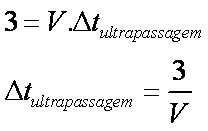
Para calcular a distância percorrida pela mosca:
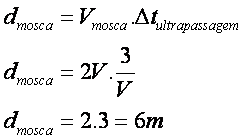
29) Em um jogo de futebol, um atleta bate uma falta comunicando à bola uma velocidade inicial Vo que forma um ângulo de 45° com o plano do chão.
A bola, após um tempo de vôo de 2,0 s, bate na parte superior da trave que está a uma altura de 2,0 m do chão.
Adote g = 10 m/s² e despreze o efeito do ar.
A altura máxima atingida pela bola é um valor mais próximo de:
(A) 3,0 m (B) 4,0 m (C) 5,0 m (D) 6,0 m (E) 7,0 m
Resolução:
A posição vertical em cada instante é dada por:
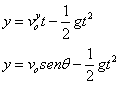
Com
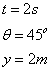
Temos:
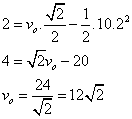
A altura máxima ocorre quando 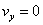 :
:
Ou ainda (por derivação):
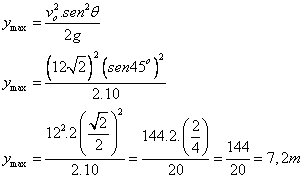
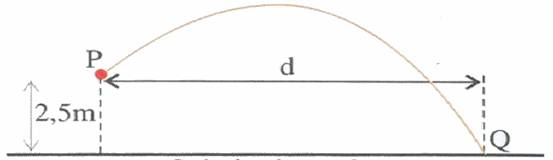
30) ma pedra é arremessada do Ponto P com uma velocidade de 10 m/s numa direção que forma um ângulo de 45 graus com a horizontal, atingindo o ponto Q conforme indicado no esquema
Considerando que a resistência do ar é desprezível, a distância d indicada no esquema, em metros, é um valor mais próximo de:
(A) 2.4
(B) 7.1
(C) 12
(D) 14
(E) 24
Resolução:
Sendo um movimento bidimensional, é conveniente decompor em duas direções: VERTICAL (y) e HORIZONTAL (x)
Na direção y, temos um MRUV com as seguintes equações:
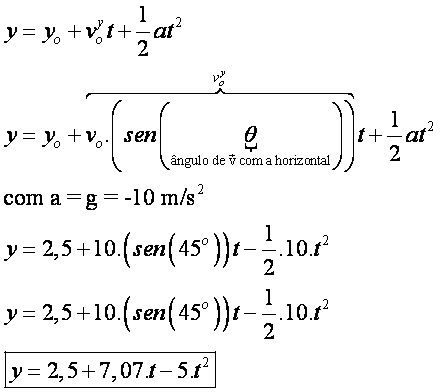
Para determinar qual o instante “t” em que a pedra chega ao solo , basta fazer y = 0, e chegamos a :
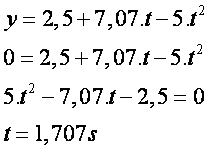
O deslocamento horizontal (“d” na figura), nada mais é que o deslocamento na direção “x” (em MRU) durante t = 1,707 s, logo:
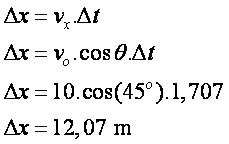
Resposta: (C)
31) Um motorista de uma transportadora recebeu seu caminhão e sua respectiva carga no km 340 de uma rodovia às 13 horas, entrou a carga no km 120 da mesma rodovia às 16 horas.Qual foi a velocidade média desenvolvida pelo caminhão?
Resolução:
Para começar devemos ter a diferença entre o km 340 e o km 120 para sabermos qual foi a distância percorrida pelo caminhão, o resultado fica: 220 e também de 16h e 13h, que fica: 3h. Agora precisamos montar nossa equação:
Vm= Δd/Δt logo, Vm= 220/3= 73,3 km/h
Esta questão, depende de seu ponto de vista, muitos dizem que a resposta é -73,3km/h por ele estar indo no sentido oposto, mais do meu ponto de vista, ele apenas teve um deslocamento de 220 km
Vm= Δd/Δt logo, Vm= 220/3= 73,3 km/h
Esta questão, depende de seu ponto de vista, muitos dizem que a resposta é -73,3km/h por ele estar indo no sentido oposto, mais do meu ponto de vista, ele apenas teve um deslocamento de 220 km
32) Submete-se um corpo de massa 5000 kg à ação de uma força constante que lhe imprime, a partir do repouso, uma velocidade de 72 km/h ao fim de 40s. Determine a intensidade da força e o espaço percorrido pelo corpo.
Resolução:
Para começar a solucionar este problema, precisamos transformar 72 km/h em X m/s
72 km/h . 3,6 = 20 m/s
Agora podemos continuar com as aquações:
Am= Δv/Δt logo, Am= 20/40= 0,5m/s²
F= ma logo, F= 5000 . 0,5= 2500N
A intensidade da Força é de 2500N
Agora precisamos saber o espaço percorrido:
Vm= Δd/Δt logo, invertendo a fórmula: Δd= VmΔt ,logo: Δd= 20 . 40= 800 m
O espaço percorrido pelo corpo foi de: 800 m
72 km/h . 3,6 = 20 m/s
Agora podemos continuar com as aquações:
Am= Δv/Δt logo, Am= 20/40= 0,5m/s²
F= ma logo, F= 5000 . 0,5= 2500N
A intensidade da Força é de 2500N
Agora precisamos saber o espaço percorrido:
Vm= Δd/Δt logo, invertendo a fórmula: Δd= VmΔt ,logo: Δd= 20 . 40= 800 m
O espaço percorrido pelo corpo foi de: 800 m
33) (VUNESP 2006) O fabricante informa que um carro, partindo do repouso, atinge 100 km/h em 10 segundos. A melhor estimativa para o valor da aceleração nesse intervalo de tempo, em m/s2, é:
a) 3,0.10-3 b) 2,8 c) 3,6 d) 9,8 e) 10
Resolução
As unidades do exercício devem ser congruentes, logo devemos fazer a transformação de km/h para m/s.

Da definição de aceleração escalar média, temos:

Obtendo como resposta a alternativa b.
34) (IFPE, 2008) Uma bicicleta tem roda traseira de raio 40 cm, catraca de raio 5 cm e coroa de raio 15 cm. Para 3(três) voltas completas da coroa, o avanço da bicicleta será: (Considere π = 3).
Resolução
A catraca e a coroa giram com a mesma velocidade linear, então:
v = ωcat.Rcat = ωcor.Rcor
2πfcat.Rcat = 2πfcor.Rcor
fcat.Rcat = fcor.Rcor
fcat . 5 = 3 . 15
fcat = 9 volta
A roda traseira e catraca giram com a mesma velocidade angular, então:
ω = 2πfr = 2πfcat
fr = fcat = 9 voltas
c = 2π.Rr.fr = 2 . 3 . 0,4 . 9 = 21,6 m
(01) o observador A vê a bola se mover verticalmente para cima e cair nas mãos do garoto.
(02) o observador B vê a bola descrever uma parábola e cair nas mãos do garoto.
(04) os dois observadores vêem a bola se mover numa mesma trajetória.
(08) o observador B vê a bola se mover verticalmente para cima e cair atrás do garoto.
(16) o observador A vê a bola descrever uma parábola e cair atrás do garoto.
Dê como resposta a soma dos números associados às proposições corretas.RESOLUÇÃO:
v = ωcat.Rcat = ωcor.Rcor
2πfcat.Rcat = 2πfcor.Rcor
fcat.Rcat = fcor.Rcor
fcat . 5 = 3 . 15
fcat = 9 volta
A roda traseira e catraca giram com a mesma velocidade angular, então:
ω = 2πfr = 2πfcat
fr = fcat = 9 voltas
c = 2π.Rr.fr = 2 . 3 . 0,4 . 9 = 21,6 m
35) (UEM-PR) Um trem se move com velocidade horizontal constante. Dentro dele estão o observador A e um garoto, ambos parados em relação ao trem. Na estação, sobre a plataforma, está o observador B parado em relação a ela. Quando o trem passa pela plataforma, o garoto joga uma bola verticalmente para cima. Desprezando-se a resistência do ar, podemos afirmar que
(01) o observador A vê a bola se mover verticalmente para cima e cair nas mãos do garoto.
(02) o observador B vê a bola descrever uma parábola e cair nas mãos do garoto.
(04) os dois observadores vêem a bola se mover numa mesma trajetória.
(08) o observador B vê a bola se mover verticalmente para cima e cair atrás do garoto.
(16) o observador A vê a bola descrever uma parábola e cair atrás do garoto.
Dê como resposta a soma dos números associados às proposições corretas.RESOLUÇÃO:
Para um referencial fixo no trem, a bola só tem um movimento vertical de sobe e desce, pois bola e o trem têm a mesma velocidade horizontal.
Para um referencial fixo na plataforma (na superfície terrestre), a bola tem um movimento horizontal mantido por inércia e um movimento vertical sob ação da gravidade; a composição desses dois movimentos origina uma trajetória parabólica.
(01) C
(02) C
(04) F
(08) F
(16) F
RESPOSTA: 03
Para um referencial fixo na plataforma (na superfície terrestre), a bola tem um movimento horizontal mantido por inércia e um movimento vertical sob ação da gravidade; a composição desses dois movimentos origina uma trajetória parabólica.
(01) C
(02) C
(04) F
(08) F
(16) F
RESPOSTA: 03
36) Um veículo percorre metade de um trecho com uma velocidade constante de 60 km/h e a outra metade do trecho com velocidade constante de 90km/h. Qual a velocidade média no percurso todo?





.gif)
ω = ωo + y.t
80. Л = 0 + y.40
40y = 80. Л
y = 80. Л/40
y = 2. Л rad/s² - aceleração angular.
φ = φo + ωo.t + y.t²/2
Δ φ = 0.40 + 2. Л.40²/2
Δ φ = 2. Л.40²/2
Δ φ = 1600.Л rad
Número de voltas = Δ φ/2. Л = 1600.Л/2. Л = 800 = 8,0.10² voltas
43) Um objeto inicia o seu movimento, a partir do repouso, deslocando-se numa trajetória circular de raio igual a 20 m. A sua aceleração tangencial tem módulo de 2 m/s2.

a)10 e 0,002
b) 30 e 0,002
c) 30 e 0,006
d) 20 e 0,006
e) 10 e 0,006
a) 50km/h
b) 75km/h
c) 72km/h
d) 80 km/h
e) 90 km/h
Solução:
A velocidade média é calculada pela distância percorrida dividida pelo tempo gasto.
Para resolver a conta é preciso trocar os tempos pelas velocidades (que são conhecidas).
Assim:
Substituindo na equação anterior:
Letra C
O exercício anterior é muito comum em exames de vestibular. Há uma fórmula já pronta para ele (nada mais é do que o MMC já feito e pronto para substituição).
37) Um carro percorre 200km em 2h. Em seguida fica 1h parado em um posto de gasolina. Após a parada o carro percorre mais 200km em 2h. Qual a velocidade escalar média no trecho total?
a) 50 km/h
b) 80 km/h
c) 100 km/h
d) 120 km/h
Solução:
Variação de posição = distância percorrida (não há preocupação no texto com vetores)
Distância = 400 km
Intervalo de tempo = 5h ( o tempo que o carro ficou parado deve ser levado em consideração, pois o intervalo de tempo é o tempo necessário para sair de um lugar e chegar ao outro)
Letra B
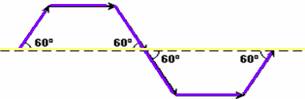
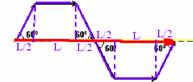
38) (CFT-CE) Uma partícula desloca-se sobre a trajetória formada pelas setas que possuem o mesmo comprimento L. A razão entre a velocidade escalar média e a velocidade vetorial média é:

a) 1/3 b) 2/3 c) 1 d) 3/2 e) 2
Resolução:
velocidade escalar --- Vme=ΔS/Δt=6L/t --- velocidade vetorial Vmv=d/t --- Lcos60o=L.12=L/2 --- Vmv=L/2 + L + L/2 + L/2 +

L + L/2=4L --- Vmv=4L/t --- t é o mesmo --- Vme/Vmv=(6L/t)/(4L/t) --- Vme/Vmv=3/2 --- R- D
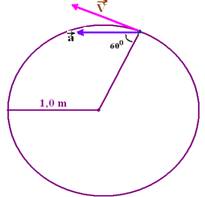
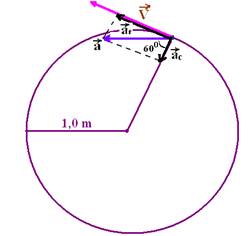
39) (UFCE-CE) Uma partícula descreve trajetória circular, de raio r=1,0m, com velocidade variável. A figura mostra a partícula em um dado instante de tempo em que sua aceleração tem módulo a=32m/s2 e aponta na direção e sentido indicados.

Nesse instante, o módulo da velocidade da partícula é:
a) 2,0m/s b) 4,0m/s c) 6,0m/s d) 8,0m/s e) 10,0m/s
Resolução:
Na figura abaixo a aceleração 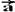 está decomposta em suas parcelas
está decomposta em suas parcelas 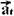 e
e 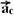

cos60o=ac/a --- 0,5=ac/32 --- ac=16m/s2 --- ac=V2/R --- 16=V2/1 --- V=4m/s --- R- B
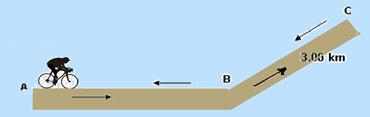
40) (ITA-SP-010) Na figura, um ciclista percorre o trecho AB com velocidade escalar média de 22,5 km/h e, em seguida, o trecho BC de 3,00 km de extensão. No retorno, ao passar em B, verifica ser de 20,0 km/h sua velocidade escalar média no percurso então percorrido, ABCB. Finalmente, ele chega em A perfazendo todo o percurso de ida e volta em 1,00 h, com velocidade escalar média de 24,0 km/h. Assinale o módulo v do vetor velocidade média referente ao percurso ABCB.

a) v = 12,0 km/h b) v = 12,00 km/h c) v = 20,0 km/h d) v = 20, 00 km/h
e) v = 36, 0 km/h
Resolução:
Cálculo do deslocamento em todo o trajeto DS = v.Dt = 24.1 = 24 km --- distância AB pode ser calculada da seguinte forma -- DS = 2.AB + 2.BC --- DS/2 = AB + BC --- AB = DS/2 – BC =24/2– 3 = 12 – 3 = 9 km --- tempo total gasto no trecho ABCB
v = DS/Dt --- Dt = DS/v = (9 + 6)/20= 15/20 --- Dt = 0,75 h --- módulo da velocidade vetorial média 9/0,75 = 12 km/h
R- A
41) A velocidade angular de um móvel em trajetória circular é diminuída de 30.π rad/s para 20. π rad/s em um intervalo de tempo igual à 2s. Sabendo que o raio do círculo mede 0,5m e o movimento é uniformemente variado; determine a acelração escalar deste móvel.
Solução:
ω = ωo + y.t
20. π = 30. π + y.2
2.y = -10. π
y = -5. π rad/s
a = y.r
a = -5.0,5
a = 2,5m/s²
42) O gráfico a seguir representa a velocidade angular, em função do tempo, de uma polia que gira ao redor de um eixo.
20. π = 30. π + y.2
2.y = -10. π
y = -5. π rad/s
a = y.r
a = -5.0,5
a = 2,5m/s²
42) O gráfico a seguir representa a velocidade angular, em função do tempo, de uma polia que gira ao redor de um eixo.
.gif)
Com base nas informações contidas no gráfico, determine a aceleração angular desta polia e a quantidade de volta que ela dá no intervalo de tempo entre 0 e 40s.
SOLUÇÃO:
ω = ωo + y.t
80. Л = 0 + y.40
40y = 80. Л
y = 80. Л/40
y = 2. Л rad/s² - aceleração angular.
φ = φo + ωo.t + y.t²/2
Δ φ = 0.40 + 2. Л.40²/2
Δ φ = 2. Л.40²/2
Δ φ = 1600.Л rad
Número de voltas = Δ φ/2. Л = 1600.Л/2. Л = 800 = 8,0.10² voltas
43) Um objeto inicia o seu movimento, a partir do repouso, deslocando-se numa trajetória circular de raio igual a 20 m. A sua aceleração tangencial tem módulo de 2 m/s2.
O objeto movimenta-se no sentido anti-horário. Após, 10 segundos.
Determine:
a) módulo da velocidade tangencial.
b) a aceleração angular.
c) a velocidade angular.
d) o comprimento do arco que o objecto percorreu durante os 10 s.
e) ângulo θ percorrido.
f) a aceleração centrípeta.
g) a aceleração total e qual é a sua direção.

Solução:
a) Vt = a x t
 π rad 180º
π rad 180º
 x 5,7º
x 5,7º
Û Vt = 2 x 10 = 20 m/s
b) at = constante = 2 m/s2
at = α x R
Û α = at/R
Û α = 2/20 = 0,1 rad/s2
c) ω (t) = ωo + α.t
Û ω (t) = 0 + 0,1 + 10
Û ω (t) = 1 rad/s
d) s (t) = so + vto.t + 1/2 .at.t2
Û s (t) = 0 + 0 + 1/2 .at.t2
Û s (t) = 1/2 x 2 x 102
Û s (t) = 100m
e) θ (t) = θo + ωo.t + 1/2 .α.t2
Û θ (t) = 0 + 0 + 1/2 .α.t2
Û θ (t) = 1/2 x 0,1 x 102
Û θ (t) = 5 rad ou 286,5º
Cálculos Auxiliares
π rad 180º
5 rad x
x = 286.5º
f) ac = v2/20
Û ac = 202/20
Û ac = 20 m/s2
g) atotal = 
Û atotal =
Û atotal = 20,1 m/s2
Û atotal =
Û atotal = 20,1 m/s2
tg (β) = at/ac
Û tg (β) = 2/20
Û tg (β) = 0,1
tg-1 (0,1) ≈ 5,7º
ou
x = 0,10 rad
Assim, em t = 10 s, o objeto:
a) Terá uma velocidade de 20 m/s.
b) A sua aceleração angular é de 0,1 rad/s2.
c) Terá uma velocidade angular de 1 rad/s.
d) Terá percorrido uma distância de s = 100m.
e) Estará na posição θ = 5 rad ou 286,5º.
f) A sua aceleração tangencial é de 2 m/s2.
g) A aceleração total é de 20,1 m/s2 e faz um ângulo de 0,10 rad com a direcção radial, apontando para o centro da trajetória.
44) (CEFET-PR) A órbita da Terra em torno do Sol, em razão da sua baixa excentricidade, é aproximadamente uma circunferência. Sabendo-se que a terra leva um ano para realizar uma volta completa em torno do Sol e que a distância média da Terra ao Sol é 150 milhões de Km, os módulos dos vetores da velocidade e aceleração em km/s e m/s² são respectivamente: *
a)10 e 0,002
b) 30 e 0,002
c) 30 e 0,006
d) 20 e 0,006
e) 10 e 0,006
Solução:
Como ω = 2 .π . f , e f = 1/T , podemos dizer também que:
ω = 2 . π / T
Um ano tem 365 dias, que possuem 24 horas, cada hora com 60 minutos, e cada 60 minutos com 3600 segundos.
Logo, em um ano, possuimos:
60 . 60 . 24 . 365 = 31536000 segundos.
Aplicando:
ω = 2 . π / 31536000
Como a velocidade linear é:
V = ω . r
O raio é 150000000:
ω = 2 . π . 150000000 / 31536000
ω = 30 km/s
Achamos em km/s pois multiplicamos rad/s por km.
Agora, sabemos que 30 km/s = 30000 m/s.
A aceleração centrípeta é calculada por:
Actp = v²/r
Agora teremos que usar o raio em metros e a velocidade em m/s. Para converter km para m, multiplique por 1000.
150.000.000 x 1000 = 150.000.000.000 m
Aplicando:
Actp = 30000²/150.000.000.000
Actp = 900.000.000/150.000.000.000
Actp = 0,006 m/s²
Letra C
ω = 2 . π / T
Um ano tem 365 dias, que possuem 24 horas, cada hora com 60 minutos, e cada 60 minutos com 3600 segundos.
Logo, em um ano, possuimos:
60 . 60 . 24 . 365 = 31536000 segundos.
Aplicando:
ω = 2 . π / 31536000
Como a velocidade linear é:
V = ω . r
O raio é 150000000:
ω = 2 . π . 150000000 / 31536000
ω = 30 km/s
Achamos em km/s pois multiplicamos rad/s por km.
Agora, sabemos que 30 km/s = 30000 m/s.
A aceleração centrípeta é calculada por:
Actp = v²/r
Agora teremos que usar o raio em metros e a velocidade em m/s. Para converter km para m, multiplique por 1000.
150.000.000 x 1000 = 150.000.000.000 m
Aplicando:
Actp = 30000²/150.000.000.000
Actp = 900.000.000/150.000.000.000
Actp = 0,006 m/s²
Letra C
Fontes: www.sofisica.com.br/
Muito bom, adorei
ResponderExcluirMaravilhoso, essas questões!
ResponderExcluirA resposta da questão 12 está errada. Não seria 50+15 = 65?
ResponderExcluirUm carro com aceleração escalar média de 50m/s , percorre um determinado percurso em 39s.Qual é a sua velocidade em km/h?
ResponderExcluirUm carro com aceleração escalar média de 50m/s , percorre um determinado percurso em 39s.Qual é a sua velocidade em km/h?
ResponderExcluir