1) (FUB-94 / Auxiliar Administrativo) Em uma loja, o metro de um determinado tecido teve seu preço reduzido de R$ 5,52 para R$ 4.60. Com R$ 126,96, a porcentagem de tecido que se pode comprar a mais é de :
| a) 19,5 % | b) 20% c) 20,5% d) 21% e) 21,5% |

2) (Banco do Brasil / Escriturário) – Quatro cães consomem semanalmente 60 kg de ração.
Assim, ao aumentarmos o número de cães em 75%, o consumo mensal, em Kg, considerando o mês de 30 dias, será de:
Montando o problema: - Sobre a ração: 04 cães --------- 60 kgs -----> por semana Por mês, então --------------> 240 kgs (considerando 04 semanas no mês) - Sobre os cães: Devemos aumentar a quantidade de cães em 75%. 04 cães x 75 % = 3
Total de cães com aumento de 75% = 7
O grande macete nesta questão é o final do problema, onde o enunciado comenta sobre o mês de 30 dias.
Ora, se fizemos os cálculos da quantidade de ração consumida a partir da questão central temos:
240 kgs x 75 % = 180 240 kgs + 180 kgs = 420 kgs (Não existe resposta nas opções do problema).
Porém 04 semanas x 7 dias = 28 dias. O enunciado fala sobre o mês de 30 dias.
Assim, temos que achar a quantidade diária consumida inicialmente de ração e depois acrescer o percentual pedido.

--> 15 kgs de ração diária x 30 dias = 450 kgs/mês
A resposta correta é a letra “c”.
3) (CEF / Escriturário) - Uma pessoa x pode realizar uma certa tarefa em 12 horas. Outra pessoa, y, é 50% mais eficiente que x. Nessas condições, o número de horas necessárias para que y realize essa tarefa é :
Solução:
O referido problema se trata de assunto muito cobrado, principalmente em concursos que envolvem nível de 1º grau, que é porcentagem.
12 horas -----> 100 % 50 % de 12 horas = 12 / 2 = 6 horas X = 12 horas --> 100 % = total de horas trabalhado Y = 50 % mais rápido que X. Então, se 50% de 12 horas equivalem a 6 horas, logo Y faz o mesmo trabalho em 6 horas. A resposta correta é a letra “c”.
4) (FUB-94 / Auxiliar Administrativo) Um disco gira a 45 rotações por minuto. Em 4 segundos, o disco dá :
| a) 3 voltas | b) 5 voltas c) 6 voltas d) 9 voltas e) 12 voltas |
Obs.: É importante notar que 1 minuto é igual a 60s.

6) Para esvaziar um compartimento com 700m3 de capacidade, 3 ralos levaram 7 horas para fazê-lo. Se o compartimento tivesse 500m3 de capacidade, ao utilizarmos 5 ralos quantas horas seriam necessárias para esvaziá-lo?
Resolução:
Primeiramente atribuamos uma letra a cada grandeza:
- M: A capacidade em metros cúbicos do compartimento;
- R: A quantidade de ralos;
- H: A duração da operação de esvaziamento em horas.
A representação para a análise do problema, obtida segundo os dados do enunciado é a seguinte:
Observe que na montagem a grandeza que estamos procurando (H), está posicionada à direita (poderia estar à esquerda), o que facilmente nos permitirá deixar a razão com o termo x isolada.
Agora vamos determinar se as grandezas são diretamente ou inversamente proporcionais em relação à grandeza H. Para isto utilizaremos setas com a mesma orientação para indicar grandezas diretamente proporcionais e com orientação inversa para indicar o oposto.
Vamos arbitrar que a orientação da grandeza H seja para baixo:
Agora vejamos se H e M são diretamente proporcionais ou não. Sabemos que ao diminuirmos a capacidade do compartimento, também iremos diminuir o tempo necessário para esvaziá-lo, então logicamente as duas grandezas são diretamente proporcionais, então a seta de M terá a mesma orientação da seta de H que é para baixo:
Determinemos se R e H são diretamente ou inversamente proporcionais. Ao aumentarmos a quantidade de ralos, automaticamente iremos diminuir o tempo necessário para esvaziar o compartimento, isto indica que as duas grandezas são inversamente proporcionais, então a seta de R será orientada para cima, direção oposta a da seta de H:
Agora devemos deixar todas as grandezas com a mesma orientação. Neste caso somente a grandeza R possui orientação oposta à da grandeza H e por isto somente ela será invertida, tanto a seta, quanto os seus elementos:
Por último podemos montar a proporção e resolvê-la:
Portanto com 5 ralos poderíamos esvaziar 500m3 em três horas.
7) Uma família com 2 duas pessoas consome 12m³ de água a cada 30 dias. Se mais uma pessoa com os mesmos hábitos de consumo se juntar a ela, quantos metros cúbicos de água eles consumirão em uma semana?
Resolução:
Como sempre, a cada uma das grandezas atribuiremos uma letra:
- F: A quantidade de famílias;
- V: O volume de água consumido;
- D: O número de dias de consumo.
Com a família passando de 2 para 3 pessoas e com o números de dias de consumo sendo reduzido de 30 para 7 dias, podemos montar a seguinte representação para a análise do problema:
Novamente posicionamos a grandeza procurada (V) à direita pelo motivo já comentado em explicações anteriores.
As grandezas são todas diretamente proporcionais à grandeza V? Vamos determinar isto agora.
Como já padronizamos, arbitremos que a orientação da grandeza V seja para baixo:
Agora vejamos se V e F são diretamente proporcionais ou não. Sabemos que ao aumentarmos a quantidade de integrantes da família, também iremos aumentar o consumo de água, sendo assim as duas grandezas são diretamente proporcionais, então a seta de F terá a mesma orientação da seta de V que é para baixo:
Determinemos se V e D são diretamente ou inversamente proporcionais. Ao diminuirmos o número de dias de consumo, também iremos diminuir o consumo de água (considerando-se apenas as duas grandezas), vemos então que as duas grandezas são diretamente proporcionais, logo a seta de D será orientada para baixo, assim como a seta de V:
Como todas as grandezas têm a mesma orientação não precisamos realizar nenhuma inversão (todas as grandezas são proporcionais entre si), resta-nos então montar a proporção e resolvê-la:
Já que nenhumas das grandezas têm orientação oposta à da grandeza procurada V, podemos simplesmente montar a proporção e resolvê-la:
Com três integrantes a família irá consumir 4,2m3 em 7 dias.
8) Um grupo de 10 trabalhadores descarregam 210 caixas de mercadoria em 3 horas. Quantas horas 25 trabalhadores precisarão para descarregar 350 caixas?
Resolução:
Primeiro passo, atribuir uma letra a cada uma das grandezas:
- T: O número de trabalhadores;
- C: A quantidade de caixas;
- D: A duração da operação de descarga.
Do enunciado temos a seguinte representação para a análise do problema:
A grandeza procurada (D) está à esquerda para que seja isolada mais facilmente no último passo.
Como já padronizamos, arbitremos que a orientação da grandeza D seja para baixo:
As grandezas D e T terão as setas com orientação oposta, isto porque ao aumentarmos o número de trabalhadores, diminuiremos o tempo da operação de descarga (considerando-se apenas as duas grandezas):
Se aumentarmos a quantidade de caixas a descarregar, também aumentaremos a duração da operação, sendo assim as grandezas D e C são diretamente proporcionais, e terão a mesma orientação de seta:
Como a grandeza T tem orientação oposta, iremos realizar a sua inversão:
Finalmente montaremos a proporção e iremos resolvê-la:
350 caixas podem ser descarregadas por 25 trabalhadores em 2 horas de trabalho.
9) Em 8 horas, 20 caminhões descarregam 160m3 de areia. Em 5 horas, quantos caminhões serão necessários para descarregar 125m3?
Solução:
Montando a tabela, colocando em cada coluna as grandezas de mesma espécie e, em cada linha, as grandezas de espécies diferentes que se correspondem:
| Horas | Caminhões | Volume |
| 8 | 20 | 160 |
| 5 | x | 125 |
Identificação dos tipos de relação: Inicialmente colocamos uma seta para baixo na coluna que contém o x (2ª coluna).
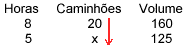
A seguir, devemos comparar cada grandeza com aquela onde está o x.
Observe que:
Aumentando o número de horas de trabalho, podemos diminuir o número de caminhões. Portanto a relação éinversamente proporcional (seta para cima na 1ª coluna).
Observe que:
Aumentando o número de horas de trabalho, podemos diminuir o número de caminhões. Portanto a relação éinversamente proporcional (seta para cima na 1ª coluna).
Aumentando o volume de areia, devemos aumentar o número de caminhões. Portanto a relação é diretamente proporcional (seta para baixo na 3ª coluna). Devemos igualar a razão que contém o termo x com o produto das outras razões de acordo com o sentido das setas.
Montando a proporção e resolvendo a equação temos:
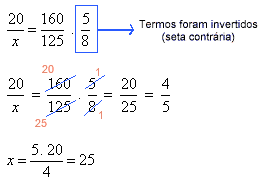 |
Logo, serão necessários 25 caminhões.
10) (ENEM-2009) Uma escola lançou uma campanha para seus alunos arrecadarem, durante 30 dias, alimentos não perecíveis para doar a uma comunidade carente da região. Vinte alunos aceitaram a tarefa e nos primeiros 10 dias trabalharam 3 horas diárias, arrecadando 12 kg de alimentos por dia. Animados com os resultados, 30 novos alunos somaram-se ao grupo, e passaram a trabalhar 4 horas por dia nos dias seguintes até o término da campanha.
Admitindo-se que o ritmo de coleta tenha se mantido constante, a quantidade de alimentos arrecadados ao final do prazo estipulado seria de
a) 920 kg. b) 800 kg. c) 720 kg. d) 600 kg. e) 570 kg.
SOLUÇÃO:
Primeiramente perceba que se os alunos arrecadaram 12kg por 10 dias então isto resulta em 12kg x 10 dias = 120 kg. Além disso 30 novos alunos se juntaram aos 20 alunos iniciais então teremos 50 alunos arrecadando nos 20 dias que ainda restam.
Ao reunir essas grandezas em colunas iremos obter:

Nesse caso como a regra de três é composta, devemos comparar a grandeza onde está a incógnita com cada umas das demais. Podemos então perceber que para aumentar o número de alimentos seria necessário que todas as outras grandezas também aumentassem.Logo,todas elas são diretamente proporcionais à grandeza alimento (Kg).Assim, não é preciso inverter a razão.

Total arrecadado = 800 + 120 (inicialmente) = 920kg
Gabarito letra A
11) Se 4 máquinas fazem um serviço em 6 dias, então 3 dessas máquinas farão o mesmo serviço em:
a) 7 dias b) 8 dias c) 9 dias d) 4,5 dias
12) Um quilo de algodão custa R$ 50,00. Um pacote de 40 gramas do mesmo algodão custa :
a) R$ 1,80 b) R$ 2,00 c) R$ 2,20 d) R$ 2,50
13) Um litro de água do mar contém 25 gramas de sal. Então, para se obterem 50 kg de sal, o número necessário de litros de água do mar será:
a) 200 b) 500 c) 2 000 d) 5 000
14) Um avião percorre 2 700 km em quatro horas. Em uma hora e 20 minutos de vôo percorrerá:
a) 675 km b) 695 km c) 810 km d) 900 km
15) Na fabricação de 20 camisetas, 8 máquinas gastam 4 horas. Para produzir 15 dessas camisetas, 4 máquinas gastariam quantas horas ?
a) 3 horas b) 6 horas c) 5 horas d) 4 horas
16) Em 7 dias, 40 cachorros consomem 100 kg de ração. Em quantos dias 3/8 deles comeriam 75 kg de ração ?
a) 10 dias. b) 12 dias. c) 14 dias. d) 18 dias
17) Três máquinas imprimem 9.000 cartazes em uma dúzia de dias. Em quantos dias 8/3 dessas máquinas imprimem 4/3 dos cartazes, trabalhando o mesmo número de horas por dia?
a) 4 dias. b) 6 dias. c) 9 dias. d) 12 dias
18) (VESTIBULINHO – SP) Numa corrida de FórmuIa 1, um corredor dá uma volta na pista em 1 minuto e 30 segundos com velocidade média de 200 km por hora. Se sua velocidade média cair para 180km por hora, o tempo gasto para a mesma volta na pista será de:
a) 2 min b) 2 min e 19 segundos
c) 1 min e 40 segundos d) 1 min e 50 segundos
19) (UMC – SP) Um carro consumiu 50 litros de álcool para percorrer 600 km. Supondo condições equivalentes, esse mesmo carro, para percorrer 840 km, consumirá :
a) 68 litros b) 80 litros c) 75 litros d) 70 litros
20) (UFMG) Uma empresa tem 750 empregados e comprou marmitas individuais congeladas suficientes para o almoço deles durante 25 dias. Se essa empresa tivesse mais 500 empregados, a quantidade de marmitas já adquiridas seria suficiente para um numero de dias igual a:
a) 10 b) 12 c) 15 d) 18
21) (Unimep – SP ) Se dois gatos comem dois ratos em dois minutos, para comer 60 ratos em 30 minutos são necessários:
a) 4 gatos b) 3 gatos c) 2 gatos d) 5 gatos e) 6 gatos
a) 4 gatos b) 3 gatos c) 2 gatos d) 5 gatos e) 6 gatos
22) ( PUC Campinas) Em uma fábrica, constatou-se que eram necessários 8 dias para produzir certo nº de aparelhos, utilizando-se os serviços de 7 operários, trabalhando 3 horas a cada dia. Para reduzir a dois dias o tempo de produção, é necessário :
a) triplicar o nº de operários
b) triplicar o nº de horas trabalhadas por dia
c) triplicar o nº de horas trabalhadas por dia e o nº de operários
d) duplicar o nº de operários
e) duplicar o nº de operários e o número de horas trabalhadas por dia.
23) (PUCCAMP-SP) Operando 12 horas por dia horas, 20 máquinas produzem 6000 peças em 6 dias. Com 4 horas a menos de trabalho diário, 15 daquelas máquinas produzirão 4.000 peças em:
a) 8 dias b) 9 dias c) 9 dias e 6 horas. d) 8 dias e 12 horas.
24) ( SANTA CASA – SP ) Sabe-se que 4 máquinas, operando 4 horas por dia, durante 4 dias, produzem 4 toneladas de certo produto Quantas toneladas do mesmo produto seriam produzidas por 6 máquinas daquele tipo, operando 6 horas por dia, durante 6 dias ?
a) 8 b) 15 c) 10,5 d) 13,5
25) (UNIV. BRASíLIA) Com 16 máquinas de costura aprontaram 720 uniformes em 6 dias de trabalho. Quantas máquinas serão necessárias para confeccionar 2.160 uniformes em 24 dias?
a) 12 máquinas b) 15 máquinas c) 18 máquinas d) 20 máquinas
26) (CEFET – 1993) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
a) 1500 toneladas b) 1800 toneladas c) 2000 toneladas d) 2200 toneladas
Gabarito:
11) B 12) B 13) C 14) D 15) B 16) C 17) B 18) C 19) D 20) C 21) A 22) E 23) A 24) D
25) A 26) B
Fontes: www.matematicadidatica.com.br/
www.ebah.com.br
Ótimas questões, me ajudaram a terminar de concluir minhas avaliações bimestrais para a escola que trabalho. Os autores do site estão de parabéns...
ResponderExcluirComo dica deixo que deixem as referências com os links das páginas consultadas e não somente o link da página principal !!!!
Os autores dos sites consultados agradecem...
Att. Romirys Cavalcante
essa questão 11 é estranha, minha resposta deu 4,5 (d), mas é obvio que está errada, pois se diminui a quantidade de máquinas tem que aumentar os dias... por favor, alguém me explique...
ResponderExcluirSimples. Quando vc for analisar as proporções precisa ver se são diretamente ou inversamente proporcionais. Ex: Quanto menos máquinas trabalhando menos dias acaba o trabalho? Não, é o contrário. Quanto menos máquinas trabalhando, mais dias serão gastos para terminar o trabalho. Assim quando for fazer a conta, vc precisa inverter as proporções. Ex:
Excluir6/x=3/4
3x=24
x=24/3
x=8.
letra b.
Boa Tarde, parabéns pelo blog, porém venho lhe informar que na questão 03 a resposta correta seria 08h. Montando uma regra de 3 simples e inversa.
ResponderExcluirAcredito que a questão 3 tenha uma resposta equivocada, a opção certa não seria a E)8? Por calcular 100% da pessoa X e 150% da pessoa Y.
ResponderExcluirNão a sposta é muito simples: Se sou 50% mais rápido vou fazer na metade do tempo.
ResponderExcluirLegal, me ajudou a resolver alguns exercícios de regra de três.
ResponderExcluirA QUESTÃO 3 ESTA ERRADA, NÃO É 6 POIS UM É 50% E NÃO 100% SE MEU CARRO ANDA A 50KM POR HORA OUTRO CARRO E 100% A MAIS QUE ELE ENTÃO O OUTRO CARRO É O DOBRO, MAS NA QUESTÃO É SÓ 50%, ENTÃO A RESPOSTA CERTA É 8 HORAS, 100% DO PRIMEIRO É 12 E 150% QUE É O SEGUNDO É 8
ResponderExcluir