Equação do primeiro e segundo grau exercícios vestibular e teoria

Equação do primeiro grau

É definido como uma equação como toda e qualquer igualdade (=) que somente pode ser satisfeita para alguns valores que estejam agregados em seus domínios.

Exemplos:

3x – 4 = 2 à o número X que é desconhecido recebe o termo de incógnita.

3y + 4 = 7 à o número Y que é desconhecido recebe o termo de incógnita.

Desta forma acima, é impossível afirmar se a igualdade do problema é verdadeira ou falsa, pois os valores das incógnitas são desconhecidos.

É possível verificar que as equações acima se tornam verdadeiras quando:

x = 2, veja:

3x – 4 = 2

3x = 2 + 4 à 3x = 6 à x = 2

y = 1, veja:

3y = 7 – 4 à 3y = 3 à y = 1

Assim os conjuntos são verdadeiros (V) e com soluções (S) = 2 e 1 respectivamente

 Agora que foi definido o termo equação, pode-se definir o que é equação do primeiro grau, como toda equação que satisfaça a forma:

ax + b = 0

Onde, tem-se:

a e b , são as constantes da equação, com a ≠ 0 (diferente de zero)

Observe:

4x + 10 = 1

a = 4

b = 10 >> constantes (4,10)

3x – 6 = 0

a = 3

b = 6 >> constantes (3,6)

Exercícios Equação  primeiro grau

1) (UFG – 2010 – 2ª Fase) Uma agência de turismo vende pacotes familiares de passeios turísticos, cobrando para crianças o equivalente a 2/3 do valor para adultos. Uma família de cinco pessoas, sendo três adultos e duas crianças, comprou um pacote turístico e pagou o valor total de R$ 8.125,00. Com base nessas informações, calcule o valor que a agência cobrou de um adulto e de uma criança para realizar esse passeio.      

2) Determine o valor de x na equação a seguir aplicando as técnicas resolutivas.

a) 3 – 2 * (x + 3) = x – 18                                 Resp: x = 5

b) 50 + (3x − 4) = 2 * (3x – 4) + 26                   Resp: x = 28/3

3) (PUC-PR) Durante determinado ano foram matriculados 100 novos alunos em um colégio. No mesmo ano, 15 alunos antigos trancaram a matrícula. Sabendo-se que, no final do ano, o número de alunos matriculados, em relação ao ano anterior, havia aumentado em 10%, o número de alunos ao final do ano era de:

a) 8 alunos          b) 10 alunos                 c) 12 alunos               d) 14 alunos                e) 15 alunos

4) (ENEM/2010) O Salto Triplo é uma modalidade do atletismo em que o atleta dá um salto em um só pé, uma passada e um salto, nessa ordem. Sendo que o salto com impulsão em um só pé será feito de modo que o atleta caia primeiro sobre o mesmo pé que deu a impulsão; na passada ele cairá com o outro pé, do qual o salto é realizado.

Disponível em: www.cbat.org.br (adaptado).

Um atleta da modalidade Salto Triplo, depois de estudar seus movimentos, percebeu que, do segundo para o

primeiro salto, o alcance diminuía em 1,2 m, e, do terceiro para o segundo salto, o alcance diminuía 1,5 m. Querendo atingir a meta de 17,4 m nessa prova e considerando os seus estudos, a distância alcançada no primeiro salto teria de estar entre

a) 4,0 m e 5,0 m.
b) 5,0 m e 6,0 m.
c) 6,0 m e 7,0 m.
d) 7,0 m e 8,0 m.
e) 8,0 m e 9,0 m.

Resolução:

Fazendo-se as considerações que:
- o alcance do segundo salto é 1,2 m menor que do primeiro salto
- o alcance do terceiro salto é 1,5 m menor que do segundo salto
- a distância alcançada no primeiro salto é x

Logo, para atingir a meta de 17,4 m, tem-se:
x + (x – 1,2) + (x – 1,2 – 1,5) = 17,4 ⇔3x = 21,3 ⇔ x = 7,1
Letra: D

5) um concurso de vestibular foi aplicado a 32.000 candidatos. sabe-se que 15.000 candidatos acertaram mais de 10 questões. sabe -se também que 20.000 candidatos acertaram menos do que 20 questões. pode se concluir que o numero de candidato que acertaram mais de 10 questões e menos de 20 questões foi igual a:

a) 2500          b) 3.000               c) 3.500            d) 4.000

Resolução:

15.000 > 10 questões
20.000 < 20 questões
??_____ 10 < x < 20 questões

(I)
15.000 > 10 questões 
Logo:
32.000 - 15.000 = 
17.000 acertaram < 10 questões.

(II)
20.000 < 20 questões
Logo:
32.000 - 20.000 = 12.000
12.000 acertaram > 20 questões

(III)
17.000 + 12.000 = 29.000
32.000 - 29.000 = 3.000
3.000 acerteram entre 10 e 20 questões

Gabarito:

1) adulto R$ 1.850,00        criança R$ 1.250,00   

2) a) x = 5   b = 28/3

3) C

4) D

5) B

Equação segundo grau

DEFINIÇÃO


Uma equação do 2º grau com uma variável tem a forma:

ax² + bx + c = 0

onde os números reais a, b e c são os coeficientes da equação, sendo que a deve ser diferente de zero. Essa equação é também chamada de equação quadrática, pois o termo de maior grau está elevado ao quadrado

x é a incógnita

a, b, e c números reais, chamados de coeficientes.

Na fórmula de Bhaskara utilizaremos somente os coeficientes. Veja:

Exemplo:

1º passo: determinar o valor do discriminante ou delta (?)
? = b² – 4 * a * c
? = (–2)² – 4 * 1 * (–3)
? = 4 + 12
? = 16

2º passo


Os resultados são x’ = 3 e x” = –1.

Exercícios resolvidos equações do segundo Grau

1) Uma tela retangular com área de 9600cm² tem de largura uma vez e meia a sua altura. Quais são as dimensões desta tela?

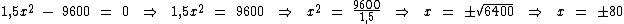
Se chamarmos de x altura da tela, temos que 1,5x será a sua largura. Sabemos que a área de uma figura geométrica retangular é calculada multiplicando-se a medida da sua largura, pela medida da sua altura. Escrevendo o enunciado na forma de uma sentença matemática temos:

x . 1,5x = 9600

Que pode ser expressa como:

1,5x² - 9600 = 0

Note que temos uma equação do 2° grau incompleta, que como já vimos terá duas raízes reais opostas, situação que ocorre sempre que o coeficiente b é igual a zero. Vamos aos cálculos:

As raízes reais encontradas são -80 e 80, no entanto como uma tela não pode ter dimensões negativas, devemos desconsiderar a raiz -80.

Como 1,5x representa a largura da tela, temos então que ela será de 1,5 . 80 = 120. Portanto:

Esta tela tem as dimensões de 80cm de altura, por 120cm de largura.

2) Resolva as equações do  2º grau abaixo:

a) x² – 7x + 4 = 0

b) 9y² – 12y + 4 = 0

3) Resolva a seguinte equação fracionária do 2º grau.

4) Comprei 4 lanches a um certo valor unitário. De outro tipo de lanche, com o mesmo preço unitário, a quantidade comprada foi igual ao valor unitário de cada lanche. Paguei com duas notas de cem reais e recebi R$ 8,00 de troco. Qual o preço unitário de cada produto?

O enunciado nos diz que os dois tipos de lanche têm o mesmo valor unitário. Vamos denominá-lo então de x.

Ainda segundo o enunciado, de um dos produtos eu comprei 4 unidades e do outro eu comprei x unidades.

Sabendo-se que recebi R$ 8,00 de troco ao pagar R$ 200,00 pela mercadoria, temos as informações necessárias para montarmos a seguinte equação:

4 . x + x . x + 8 = 200

Ou então:

Como x representa o valor unitário de cada lanche, vamos solucionar a equação para descobrimos que valor é este:

As raízes reais da equação são -16 e 12. Como o preço não pode ser negativo, a raiz igual -16 deve ser descartada. Assim:

O preço unitário de cada produto é de R$ 12,00.

5) O quádruplo de um número, diminuído de três, é igual a 99. Qual é esse número ?

4x - 3 = 99

4x - 3 + 3 = 99 + 3

4x = 102

4x / 4 = 102 / 4

x = 51 / 2 ou x = 25,5

Resposta: O número é 51/2 ou 25,5.

Exercícios equação 2º Grau

1) O triplo do quadrado do número de filhos de Pedro é igual a 63 menos 12 vezes o número de filhos. Quantos filhos Pedro tem?

a) 1                            b) 2                            c) 3                        d) 4                             e) 5  

2) Um dardo é lançado da origem, segundo um referencial dado, e percorre a trajetória de uma parábola. A função que representa essa parábola é y = -x² + 4x. Quais são as coordenadas do ponto no qual esse dardo atinge sua altura máxima?

3) Na equação do 2º grau ax² + bx + c = 0, os números a e c têm sinais contrários. Pode-se afirmar que:
 
a) A equação tem duas raízes reais de sinais contrários.
b) A equação tem duas raízes reais positivas.
c) A equação tem duas raízes reais negativas.
d) A equação pode não ter raízes reais.
e) n.d.a.

4) (PUCCAMP) Se v e w são as raízes da equação x² + ax + b = 0, onde a e b são coeficientes reais, então v² + w² é igual a:

a) a² - 2b
b) a² + 2b
c) a² - 2b²
d) a² + 2b²
e) a² - b²

5)  Para x = – 3 , a expressão 2x² + 3x é igual a 9. Um outro valor real de x, para o qual essa expressão também é igual a 9, é:

 a) 3

b) 2

c) 3/2

d) 2/3

6) Se multiplicarmos o quadrado de um número negativo por 3 e subtrairmos 2 do resultado, obtemos o quíntuplo do mesmo número. Esse número está compreendido entre:

a) – 4 e – 3.

b) – 3 e – 2.

c) – 2 e – 1.

d) – 1 e 0.

7) A sentença (ax – 1).(x + a) = (ax -1).(2x + a) é uma equação do 2º grau em x. Se a ≠ 0 e x ≠ 0,  então é raiz da equação a expressão:

a) 3/a

b) 2a

c) 1/a

d) 3a/2

 8) Se  são raízes de uma equação do 2º grau, essa equação é:

a) x² – x – 6 = 0

b) x² + x – 6 = 0

c) x² +2x – 6 = 0

d) x² – 2x – 6 = 0

9) A equação cuja soma das raízes é -2/3 é:

a) 3a² – 2a + 1 = 0

b) 4a² + 6a – 1 = 0

c) 6a² + 4a – 1 = 0

d) 2a² – 3a + 1 = 0

10) Dada a equação 5x² + 7x + 1 = 3x² + 2x + 1, uma de suas raízes reais é:

a) 3

b) 2/3

c) – 1

d) -5/2

11) A soma das raízes positivas da equação x² (x² – 6) = - 5 é:

a) 

b) 

c) 6

d) 5

12) Um número positivo, elevado ao quadrado, é igual a ele mesmo aumentado de 2. Esse número é:

a) ímpar e composto

b) par e composto

c) ímpar e primo

d) par e primo

Gabarito:

1) C  2)  xv = 2 e yv = 4  3) A  4) A  5) C  6) D   7) C  8) D  9) C  10) D  11) A  12) D

Fonte: http://www.cpteorema.com/eq_problemas_2grau.htm
          http://www.brasilescola.com/