Funções Trigonométricas: Resumo com exemplos

Funções Trigonométricas

Função Seno

O domínio dessa função é R e a imagem é Im [ -1,1] ou im(f) = {y E R/-1 < y < 1} ; uma vez que, na circunferência trigonométrica o raio é unitário e, pela definição do seno, –1 £ sen x £ 1.

Indicamos essa função por:

f(x) = sen(x)

Na função seno, temos: sen x = sen (x + K . 2π), K E Z para x E R. O menor valor positivo de K . 2π ocorre quando K = 1. Portanto: sen x = sen (x + 1 . 2π)

Dessa forma concluímos que: A função y = sen x é periódica de período 2π.

Sinal da função Seno

Analisando o sinal da função y = sen x, em cada um dos quadrantes, temos:

f(x) = sen x é positiva no 1° e 2° quadrantes (ordenada positiva)

f(x) = sen x é negativa no 3° e 4° quadrantes (ordenada negativa)

Gráfico da função seno

O gráfico da função y = sen x é chamado senóide.

Resumindo, temos:

1- Função y = sen x ou f(x) = sen x

2- O domínio é D(f) = R

3- O conjunto-imagem é im(f) = [-1;1].

4- A função é periódica, de período 2π.

5- O sinal da função é:

                  positivo no 1º e 2º quadrantes;

                  negativo no 3º e 4º quadrantes.

6- A função é ímpar.

7- A função é crescente no 1º e 4º quadrantes e decrescente no 2º e 3º quadrantes.

            

Exemplo: Mostre que a função definida por f(x)=sen(x) é ímpar, isto é, sen(-a)=-sen(a), para qualquer a real.

sen(-a)	=	sen(2-a)
	=	sen(2).cos(a) - cos(2).sen(a)
	=	0 . cos(a) - 1 . sen(a)
	=	-sen(a)

Exemplo2: Qual o domínio e o conjunto imagem da função y = sen 4x?

Solução:
Podemos escrever: 4x = sen y. Daí, vem:
Para x: -1 £ 4x £ 1 Þ -1/4 £ x £ 1/4. Portanto, Domínio = D = [-1/4, 1/4].
Para y: Da definição vista acima, deveremos ter -p /2 £ y £ p /2.
Resposta:  D = [-1/4, 1/4] e Im = [-p /2, p /2].

Função Cosseno

O domínio dessa função é R e a imagem é Im [ -1,1] ou ainda Im(f) = {y E R/ -1 < y < 1}; visto que, na circunferência trigonométrica o raio é unitário e, pela definição do cosseno, –1 £ cos x £ 1.

O período da função cos x é 2π, pois Ax E R temos cos x = cos (x + K 2π), com K E Z e o menor valor positivo de K.2π, tal que isso ocorra, é 1.2π.

Sinal da função Cosseno

Estudando o sinal da função y = cos x em cada um dos quadrantes, temos:

f(x) = cos x é positiva no 1° e 2° quadrantes (abscissa positiva)

f(x) = cos x é negativa no 3° e 4° quadrantes (abscissa negativa)   

Gráfico da função Cosseno

Resumindo temos:

1- Função y = cos x ou f(x) = cos x

2- O domínio é D(f) = R

3- O conjunto imagem é Im(f) = [-1;1]

4- A função é periódica de período 2π.

5- O sinal da função é:

                    positivo no 1º e 4º quadrantes;

                    negativo no 2º e 3º quadrantes.

6 - A função é função par.

7- A função é crescente no 3º e 4º quadrantes e decrescente no 1° e 2º quadrantes.

Exemplo: Mostre que a função definida por f(x)=cos(x) é par, isto é, cos(-a)=cos(a), para qualquer a real.

cos(-a)	=	cos(2-a)
	=	cos(2).cos(a) + sen(2).sen(a)
	=	1.cos(a) + 0.sen(a)
	=	cos(a)

Função Tangente

O domínio dessa função são todos os números reais, exceto os que zeram o cosseno pois não existe cosx = 0 e a imagem é tg x; Im(tg x) = R ou  .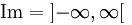

A função é periódica , de período π.

Sinal da Função Tangente

Valores positivos nos quadrantes ímpares(1º e 3°) 
Valores negativos nos quadrantes pares(2º e 4º)

Crescente em cada valor. 

Gráfico da Função Tangente

                           função chamada tangentóide

Resumindo temos:

1- Função y = tg x ou f(x) = tg x

2- O domínio é D(f) = {x E R/ x# π/2 + k . π, k E Z}

3- O conjunto imagem é Im(f) = R.

4- A função é periódica, de período π.

5- O sinal da função é:

                   positivo no 1º e 3º quadrantes;

                   negativo no 2º e 4º quadrantes.

6- A função é uma função Ímpar.

7- A função é crescente em todos os quadrantes.

exemplo: Determine o valor de tan(-35/4).

tan(-35/4)=tan(-35/4+5.2)=tan(5/4)

Portanto

tan(-35/4)=1

Função Cotangente

O domínio da função y = cotg x é R - {n . π, n E Z} e a imagem Im(f)  = R.
A função é periódica, de período  π. Indicamos essa função por: y = f(x) =  cotg x. A função y = cotg x é ímpar. Vejamos: cotg (-x) = - cotg x

Sinal da função cotangente

A função cotangente tem os mesmos sinais da tangente, ou seja, positivo no 1º e 3º quadrantes e negativo no 2º e 4º quadrantes.



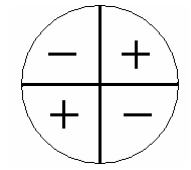
Gráfico da função cotangente



Função secante
A função secante de x, é definida como o inverso do cosseno: 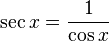. O domínio da função é D(f) = R - { π/2 + n .  π, n E Z} e a imagem Im(f) = { y E R/ y £ -1 ou y ³1}.
O período da função secante é 2π. É também uma função par, pois para todo x onde a secante é definida, tem-se que: sec(x) = sec(-x)

Sinal da função secante

A função secante tem os mesmos sinais da função cosseno, ou seja, positiva no 1° e 4° quadrantes e negativa no 2º e 4º quadrantes.



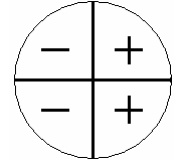
Gráfico da função Secante



Função Cossecante

A função cossecante de x, é o inverso do seno: cossec x = 1/sen x. O domínio da função é R - {n . π, n E Z} e a imagem Im(f) = {y em R: y < -1    ou    y > 1}.
O período da função é 2 .π. Assim como a função cotangente, a função cossecante é ímpar pois para todo x onde a cossecante está definida, tem-se que:
cossec (- x) = - cossec x
Sinal da função Cossecante

A função cossecante tem os mesmos sinais da função seno, ou seja,  positivo no 1º e 2º quadrantes e negativo no 3º e 4º quadrantes.



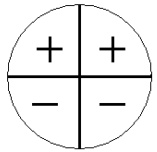
Gráfico da função Cossecante