A função exponencial é aquela na qual sua parte variável representada por x se encontra no expoente. Observe:
y = 3 x
y = 5 x + y = 0,9 x
A lei de formação de uma função exponencial indica que a base elevada ao expoente x precisa ser maior que zero e diferente de um, conforme a seguinte notação:
Representação da Função Exponencial no Plano Cartesiano
Para representarmos graficamente uma função exponencial, podemos fazê-lo da mesma forma que fizemos com a função quadrática, ou seja, arbitrarmos alguns valores para x, montarmos uma tabela com os respectivos valores de f(x), localizarmos os pontos no plano cartesiano e traçarmos a curva do gráfico.
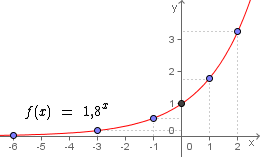
Para a representação gráfica da função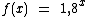 
arbitraremos os seguinte valores para x:
-6, -3, -1, 0, 1 e 2.
Montando a tabela temos:
| x | y = 1,8x |
|---|---|
| -6 | y = 1,8-6 = 0.03 |
| -3 | y = 1,8-3 = 0.17 |
| -1 | y = 1,8-1 = 0.56 |
| 0 | y = 1,80 = 1 |
| 1 | y = 1,81 = 1.8 |
| 2 | y = 1,82 = 3.24 |
Ao lado temos o gráfico desta função exponencial, onde localizamos cada um dos pontos obtidos da tabela e os interligamos através da curva da função:
f: R→R tal que y = a x, sendo que a > 0 e a ≠ 1.
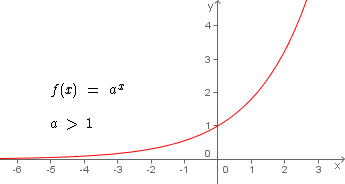
Função crescente
No gráfico da função ao lado podemos observar que à medida que x aumenta, também aumenta f(x) ou y. Graficamente vemos que a curva da função é crescente.
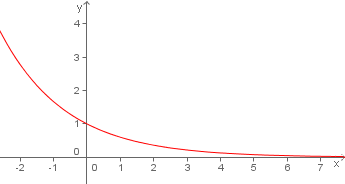
Função decrescente
Se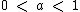 
temos uma função exponencial decrescente em todo o domínio da função.
Neste outro gráfico podemos observar que à medida quex aumenta, y diminui. Graficamente observamos que a curva da função é decrescente.
PROPRIEDADES DA FUNÇÃO EXPONENCIAL
Se a, x e y são dois números reais quaisquer e k é um número racional, então:
- ax ay= ax + y
- ax / ay= ax - y
- (ax) y= ax.y
- (a b)x = ax bx
- (a / b)x = ax / bx
- a-x = 1 / ax
Estas relações também são válidas para exponenciais de base e (e = número de Euller = 2,718...)
- y = ex se, e somente se, x = ln(y)
- ln(ex) =x
- ex+y= ex.ey
- ex-y = ex/ey
- ex.k = (ex)k
gostei da explicaçao foi muito utel para mim
ResponderExcluir