Espaço amostral e evento são termos ligados à probabilidade, ciência que estuda as chances de um fenômeno acontecer. A realização de um experimento repetidas vezes respeitando as mesmas condições, não deve apresentar os mesmos resultados. É nesse aspecto que a probabilidade conceitua suas regras, demonstrando os resultados através de números, em forma de porcentagem. Para o cálculo da probabilidade de algo acontecer, precisamos entender os termos: espaço amostral e evento.
Espaço amostral é o conjunto estabelecido por todos os possíveis resultados de um experimento. Por exemplo, no lançamento de uma moeda, o espaço amostral é dado por “cara” ou “coroa”. No lançamento de um dado, o espaço amostral é representado pelas faces enumeradas 1, 2, 3, 4, 5 e 6. Em um baralho de cartas, o espaço amostral envolve 52 cartas.
Evento: é um conjunto de resultados do experimento, em termos de conjuntos, é um subconjunto S. em particular, S e Φ (conjunto vazio) são eventos. S é dito o evento certo e Φ o evento impossível.
Se usarmos as operações com conjuntos, podemos formar novos eventos:
a) A ∩ B → é o evento que ocorre se A ocorreu ou B ocorre ou ambos ocorrem;
b) A ∪ B → evento que ocorre se A e B ocorrerem;
c) Ā → é o evento que ocorre se A não ocorre.
Exemplo: Considere o experimento: jogar duas moedas e observar os resultados:
S = {(c, c), (c, k), (k, c), (k, k)}
Evento A: ocorrer faces iguais.
Logo A = {(c, c), (k, k)}
Exemplo 2:
Considere o experimento “lançar 2 dados simultaneamente” .
O espaço amostral será
E = { (1,1) , (1,2) , (1,3) , (1,4) , (1,5) , (1,6) ,
(2,1) , (2,2) , (2,3) , (2,4) , (2,5) , (2,6) ,
(3,1) , (3,2) , (3,3) , (3,4) , (3,5) , (3,6) ,
(4,1) , (4,2) , (4,3) , (4,4) , (4,5) , (4,6) ,
(5,1) , (5,2) , (5,3) , (5,4) , (5,5) , (5,6) ,
(6,1) , (6,2) , (6,3) , (6,4) , (6,5) , (6,6) } e n(E) = 36.
Considere o evento A: a soma dos pontos é 5.
Então esse evento será representado pelo conjunto
A = { (1,4) , (4,1) , (2,3) , (3,2) }
Eventos mutuamente exclusivos
Eventos mutuamente exclusivos são aqueles que não podem ocorrer simultaneamente. Portanto dois eventos A e B são mutuamente exclusivos se AB = Φ
Exemplo: Considere o experimento: jogar um dado e observar o resultado.
S = {1, 2, 3, 4, 5, 6}
Sejam os eventos:
A = ocorrer número par e B = ocorrer números impar.
Logo: A = {2, 4, 6}, B = {1, 3, 5}
A e B são considerados mutuamente exclusivos pois A ∩ B = Φ
OPERAÇÕES COM EVENTOS
Considerando A e B dois eventos quaisquer de um espaço amostral E, e representando por x um ponto amostral de E, diremos que:
i) x  A
A  B
B  A ou B ocorrer (ou ambos)
A ou B ocorrer (ou ambos)
 A
A  B
B  A ou B ocorrer (ou ambos)
A ou B ocorrer (ou ambos)
ii) x  A
A  B
B  A e B ocorrerem simultaneamente
A e B ocorrerem simultaneamente
 A
A  B
B  A e B ocorrerem simultaneamente
A e B ocorrerem simultaneamente
iii) x 
 = E - A
= E - A  A não ocorrer
A não ocorrer

 = E - A
= E - A  A não ocorrer
A não ocorrer
iv) x  A – B
A – B  A ocorre, mas B não ocorre
A ocorre, mas B não ocorre
 A – B
A – B  A ocorre, mas B não ocorre
A ocorre, mas B não ocorre
Isto é,
i) A  B = { x
B = { x E | x
E | x A ou x
A ou x B } (reunião de conjuntos)
B } (reunião de conjuntos)
 B = { x
B = { x E | x
E | x A ou x
A ou x B } (reunião de conjuntos)
B } (reunião de conjuntos)
ii) A  B = { x
B = { x E | x
E | x A e x
A e x B } (intersecção de conjuntos)
B } (intersecção de conjuntos)
 B = { x
B = { x E | x
E | x A e x
A e x B } (intersecção de conjuntos)
B } (intersecção de conjuntos)
iii)  = E - A = { x
= E - A = { x E | x
E | x A } (complementar de A)
A } (complementar de A)
 = E - A = { x
= E - A = { x E | x
E | x A } (complementar de A)
A } (complementar de A)
iv) A – B = { x E | x
E | x A mas x
A mas x B } (diferença de conjuntos)
B } (diferença de conjuntos)
 E | x
E | x A mas x
A mas x B } (diferença de conjuntos)
B } (diferença de conjuntos)
Quando acontece A  B = Φ (conjunto vazio), dizemos que os eventos A e B são mutuamente exclusivos.
B = Φ (conjunto vazio), dizemos que os eventos A e B são mutuamente exclusivos.
 B = Φ (conjunto vazio), dizemos que os eventos A e B são mutuamente exclusivos.
B = Φ (conjunto vazio), dizemos que os eventos A e B são mutuamente exclusivos.
EXEMPLO: Seja E = {1,2,3,4,5,6} o espaço amostral do experimento "tirar uma
bola de uma urna, contendo 6 bolas numeradas de 1 a 6, e
observar o número obtido".
Considerando os eventos A = {1,2} , B = {1,3,5} e C ={2,4,6}, temos que
A  B = {1,2,3,5}
B = {1,2,3,5}
 B = {1,2,3,5}
B = {1,2,3,5}
A  B = {1}
B = {1}
 B = {1}
B = {1}
A – B = {2}
B – A = {3,5}
B  C = Φ , (portanto B e C são mutuamente exclusivos)
C = Φ , (portanto B e C são mutuamente exclusivos)
 C = Φ , (portanto B e C são mutuamente exclusivos)
C = Φ , (portanto B e C são mutuamente exclusivos)Questões sobre espaço amostral e eventos
1) Uma bola será retirada de uma sacola contendo 5 bolas verdes e 7 bolas amarelas. Qual a probabilidade desta bola ser verde?
Neste exercício o espaço amostral possui 12 elementos, que é o número total de bolas, portanto a probabilidade de ser retirada uma bola verde está na razão de 5 para 12.
Sendo S o espaço amostral e E o evento da retirada de uma bola verde, matematicamente podemos representar a resolução assim:
A probabilidade desta bola ser verde é 5/12
2) O jogo de dominó é composto de peças retangulares formadas pela junção de dois quadrados. Em cada quadrado há a indicação de um número, representado por uma certa quantidade de bolinhas, que variam de nenhuma a seis. O número total de combinações possíveis é de 28 peças. Se pegarmos uma peça qualquer, qual a probabilidade dela possuir ao menos um 3 ou 4 na sua face?
Chamemos de A o evento da ocorrência de um 3:
Chamemos de A o evento da ocorrência de um 3:
A = { (0, 3), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3) }
Chamemos de B o evento da ocorrência de um 4:
B = { (4, 0), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6) }
Veja que o elemento (4, 3) integra os dois eventos, logo 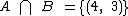 .
.
Calculando as probabilidades de A, B e da intersecção, temos:
Finalmente para o cálculo da probabilidade desejada vamos utilizar a fórmula da probabilidade da união de dois eventos:
Repare que 13 é o número total de peças que possuem 3 ou 4, desconsiderando-se a ocorrência que se repete (o (4 ,3) da intersecção dos dois eventos).
A probabilidade de ela possuir ao menos um 3 ou 4 na sua face é 13/28.
3) Alguns amigos estão em uma lanchonete. Sobre a mesa há duas travessas. Em uma delas há 3 pastéis e 5 coxinhas. Na outra há 2 coxinhas e 4 pastéis. Se ao acaso alguém escolher uma destas travessas e também ao acaso pegar um dos salgados, qual a probabilidade de se ter pegado um pastel?
A probabilidade de escolhermos 1 dentre 2 travessas é igual 1/2.
A probabilidade de escolhermos um pastel na primeira travessa é 3 em 8, ou seja, é 3/8 e como a probabilidade de escolhermos a primeira travessa é 1/2, temos:
A probabilidade de escolhermos um pastel na segunda travessa é 4 em 6, isto é 4/6 e como a probabilidade de escolhermos a segunda travessa é igual a 1/2, temos:
Então a probabilidade de escolhermos um pastel é igual a:
4) Três moedas são lançadas ao mesmo tempo. Qual é a probabilidade de as três moedas caírem com a mesma face para cima?
Através do princípio fundamental da contagem podemos determinar o número total de agrupamentos ao lançarmos três moedas.
Como cada moeda pode produzir dois resultados distintos, três moedas irão produzir 2 . 2 . 2 resultados distintos, ou seja, poderão produzir 8 resultados distintos. Este é o nosso espaço amostral.
Dentre as 8 possibilidades do espaço amostral, o evento que representa todas as moedas com a mesma face para cima possui apenas 2 possibilidades, ou tudo cara ou tudo coroa, então a probabilidade será dada por:
Na questão 3 há um erro. 2x8 = 16 ok, mas na parte da segunda travessa o 2x6 é igual a 12 e não a 3...
ResponderExcluir