Estudaremos agora as relações trigonométricas no triângulo retângulo com exemplos para um melhor aprendizado.
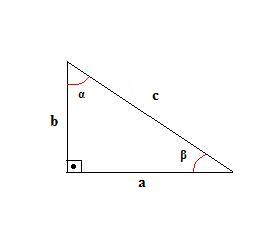
Observe a figura abaixo que representa um triângulo retângulo.
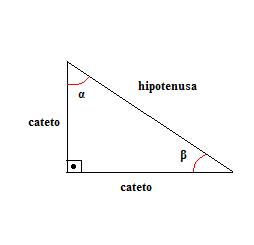
Note que o maior lado é denominado de hipotenusa e os outros dois lados de catetos. A hipotenusa é o lado que fica oposto ao ângulo reto (ângulo de 90o). Além do ângulo reto, há dois ângulos agudos, α e β. A trigonometria estabelece relações entre os ângulos agudos do triângulo retângulo e as medidas de seus lados. Vejamos quais são essas relações.
O seno de um ângulo no triângulo retângulo é a razão entre o cateto oposto e a hipotenusa.
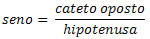
O cosseno de um ângulo no triângulo retângulo é a razão entre o cateto adjacente e a hipotenusa.
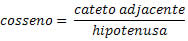
A tangente de um ângulo no triângulo retângulo é a razão entre o cateto oposto e o cateto adjacente.
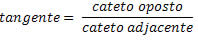
Definidas as razões trigonométricas, obtemos as seguintes igualdades para o triângulo retângulo abaixo:

Ângulos
|
30°
|
45°
|
60°
|
Seno
|
1/2
| ||
Cosseno
|
1/2
| ||
Tangente
|
1
|
Observação importante:
- sen2 α + cos2 α = 1
- tg α =sen α / cos α
Exemplo 1:
Calcular x, dados:
sen 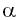 = 0,8; cos
= 0,8; cos 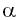 = 0,6; tg
= 0,6; tg 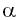 = 0,75
= 0,75
Solução:
Primeiro é preciso decidir qual das três razões trigonométricas dadas convém ao problema.
Observe que a hipotenusa é conhecida e que x é a medida do cateto adjacente a 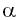 . Como hipotenusa e cateto adjacente são relacionados pelo cosseno, temos:
. Como hipotenusa e cateto adjacente são relacionados pelo cosseno, temos:
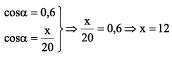
Sabendo que sen α =1/2 , determine o valor de x no triângulo retângulo abaixo:
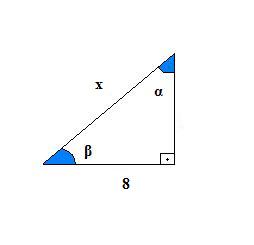
Solução: A hipotenusa do triângulo é x e o lado com medida conhecida é o cateto oposto ao ângulo α. Assim, temos que:
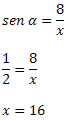
Nenhum comentário:
Postar um comentário