Unidades de medidas
As unidades de medidas é um assunto muito presente em concursos e vestibulares e por isso mesmo estudaremos esse assunto de forma mais detalhada.
Unidade no SI: m
Tabela 1.0
Medida padrão de massa
É representado simbolicamente pela letra “g” (lê-se o grama)
Unidade no SI: Kg
Exemplo:
Inicialmente devemos sempre lembrar que quando nos referimos a palavra “medir” estamos sempre fazendo uma comparação com uma grandeza padrão.
A necessidade da padronização das medidas no mundo e da criação de um sistema mais preciso deram origem ao Sistema Métrico Decimal em 1791. Porém mais tarde o mesmo fora substituído pelo- International System of Units (SI) -conhecido por nós como Sistema Internacional de Unidades.
A necessidade da padronização das medidas no mundo e da criação de um sistema mais preciso deram origem ao Sistema Métrico Decimal em 1791. Porém mais tarde o mesmo fora substituído pelo- International System of Units (SI) -conhecido por nós como Sistema Internacional de Unidades.
Medida padrão de Comprimento
É representado simbolicamente pela letra “m”(lê-se metro)
É representado simbolicamente pela letra “m”(lê-se metro)
Unidade no SI: m
Tabela 1.0
| km | hm | dam | m | dm | cm | mm |
| ÷10 | ÷10 | ÷10 | 1 | X10 | X10 | X10 |
Múltiplos do Metro:
- dam : Decâmetro -> equivale a 10 vezes a grandeza padrão”m”
- hm: Hectômetro -> Equivale a 102 vezes a grandeza padrão “m”
- km: Quilômetro -> Equivale a 103 vezes a grandeza padrão “m”
Submúltiplos do Metro:
- dm: Decímetro -> Equivale a 10-1 (1/10) vezes a grandeza padrão “m”
- cm: Centímetro -> Equivale a 10-2 (1/100) vezes a grandeza padrão “m”
- mm: Milímetro -> Equivale a 10-3 (1/1000) vezes a grandeza padrão “m”
Exemplo 1:
Converta 2,5 metros em centímetros
Para convertermos 2,5 metros em centímetros, devemos multiplicar (porque na tabela metro está à esquerda de centímetro) 2,5 por 10 duas vezes, pois para passarmos de metros para centímetros saltamos dois níveis à direita. Primeiro passamos de metros para decímetros e depois de decímetros para centímetros:
Para convertermos 2,5 metros em centímetros, devemos multiplicar (porque na tabela metro está à esquerda de centímetro) 2,5 por 10 duas vezes, pois para passarmos de metros para centímetros saltamos dois níveis à direita. Primeiro passamos de metros para decímetros e depois de decímetros para centímetros:
2,5 m * 10 * 10 = 250 cm
Isto equivale a passar a vírgula duas casas para a direita.
Portanto:
2,5 m é igual a 250 cm.
Exemplo 2:
Converta 4 km para decímetro
Para convertemos 4 km para m, devemos multiplicar (porque na tabela quilômetro está à esquerda de decímetro) 4 por 10 quatro vezes, pois para passarmos de quilômetros para decímetros saltamos quatro níveis à direita.
4 km * 10 * 10 * 10 * 10 = 40.000 dm
Portanto:
4 km é igual a 40.000 dm
Pé, jarda e Polegada não pertencem ao SI, são definidos pelo sistema inglês de unidades.
- 1 Polegada (in) = 2,54 cm
- 1 Pé (ft) = 30,48 cm
- 1 Jarda (yd) = 91,44 cm
Existem outras unidades de medida mas que não pertencem ao sistema métrico decimal. Vejamos as relações entre algumas dessas unidades e as do sistema métrico decimal:
1 polegada = 25 milímetros
1 milha = 1 609 metros
1 légua = 5 555 metros
1 pé = 30 centímetros
1 milha = 1 609 metros
1 légua = 5 555 metros
1 pé = 30 centímetros
Obs: valores aprximados
Medida padrão de massa
É representado simbolicamente pela letra “g” (lê-se o grama)
Unidade no SI: Kg
| kg (Quilograma) | hg (Hectograma) | dag (Decagrama) | g (grama) | dg (Decigrama) | cg (Centigrama) | mg (Miligrama) |
| ÷10 | ÷10 | ÷10 | 1 | X10 | X10 | X10 |
Obs: 1ton=1000kg
As regras de conversão se aplicam conforme ensinado acima.
Passe 5.200 gramas para quilogramas
Unidade no SI: m2
 Portanto:
Portanto:
0,000000000000000014 km³, ou a 1,4 x 10-17 km³ se expresso em notação científica equivalem a 14 mm³.
Equivalência entre medidas de volume e medidas de capacidade
Um cubo com aresta de 10 cm terá um volume de 1.000 cm³, medida esta equivalente a 1 l.
Como 1.000 cm³ equivalem a 1 dm³, temos que 1 dm³ equivale a 1 l.
Como um litro equivale a 1.000 ml, podemos afirmar que 1 cm³ equivale a 1 ml.
1.000 dm³ equivalem a 1 m³, portanto 1 m³ é equivalente a 1.000 l, que equivalem a 1 kl.
Década – 10 anos
Ano – aproximadamente 365 dias
Mês – 30 e 31 dias
Dia – 24 horas
Hora – 60 minutos
Minuto – 60 segundos
Para passarmos 5.200 gramas para quilogramas, devemos dividir (porque na tabela grama está à direita de quilograma) 5.200 por 10 três vezes, pois para passarmos de gramas para quilogramas saltamos três níveis à esquerda. Primeiro passamos de grama para decagrama, depois de decagrama para hectograma e finalmente de hectograma para quilograma:
5200 g : 10 : 10 : 10 = 5,2 kg
Isto equivale a passar a vírgula três casas para a esquerda.
Portanto:
5.200 gramas é igual 5,2 kg
5200 g : 10 : 10 : 10 = 5,2 kg
Isto equivale a passar a vírgula três casas para a esquerda.
Portanto:
5.200 gramas é igual 5,2 kg
Medida padrão de superfície ou área
É representado simbolicamente por “m2” (lê-se metro quadrado). Considera-se uma unidade derivada do metro.
É representado simbolicamente por “m2” (lê-se metro quadrado). Considera-se uma unidade derivada do metro.
Unidade no SI: m2
| Km2 | Hm2 | Dam2 | M2 | Dm2 | Cm2 | Mm2 |
| ÷100 | ÷100 | ÷100 | 1 | X100 | X100 | X100 |
ATENÇÃO: Para convertermos agora devemos ver que é necessário “pularmos” de duas em duas “casas”.
Exemplo:
Passe 50 dm² para hectômetros quadrados
Para passarmos de decímetros quadrados para hectômetros quadrados, passaremos três níveis à esquerda. Dividiremos então por 100 três vezes:
50 dm² : 100 : 100 : 100 = 0,00005 hm²
Isto equivale a passar a vírgula seis casas para a esquerda.
Portanto:
50 dm² é igual a 0,00005 hm².
Áreas das figuras geométricas planas
Constantemente no estudo de gráficos, precisamos determinar a área compreendida entre a curva e o eixo-x. Daremos aqui as fórmulas, para o cálculo da área, das figuras mais utilizadas na Física.
.jpg)
Passe 50 dm² para hectômetros quadrados
Para passarmos de decímetros quadrados para hectômetros quadrados, passaremos três níveis à esquerda. Dividiremos então por 100 três vezes:
50 dm² : 100 : 100 : 100 = 0,00005 hm²
Isto equivale a passar a vírgula seis casas para a esquerda.
Portanto:
50 dm² é igual a 0,00005 hm².
Áreas das figuras geométricas planas
Constantemente no estudo de gráficos, precisamos determinar a área compreendida entre a curva e o eixo-x. Daremos aqui as fórmulas, para o cálculo da área, das figuras mais utilizadas na Física.
.jpg)
Medida padrão de volume ou capacidade
É representado simbolicamente por “m3” (lê-se metro cúbico). Considera-se uma
unidade derivada do metro.
É representado simbolicamente por “m3” (lê-se metro cúbico). Considera-se uma
unidade derivada do metro.
| Km3 | Hm3 | Dam3 | M3 | Dm3 | Cm3 | Mm3 |
| ÷1000 | ÷1000 | ÷1000 | 1 | X1000 | X1000 | X1000 |
Obs:1dm3=1L
ATENÇÃO: Para convertermos devemos ver que é necessário “pularmos “de três em três “casas”.
Exemplo:
Quantos quilômetros cúbicos equivalem a 14 mm3?
Para passarmos de milímetros cúbicos para quilômetros cúbicos, passaremos seis níveis à esquerda. Dividiremos então 14 por 1000 seis vezes:
0,000000000000000014 km³, ou a 1,4 x 10-17 km³ se expresso em notação científica equivalem a 14 mm³.
Algumas conversões importantes:
Grandeza: Tempo
SI= segundos “s”
1min=60s
60min=1hora
1hora=3600s
Temperatura
SI= Kelvin “K” (escala absoluta)
Um cubo com aresta de 10 cm terá um volume de 1.000 cm³, medida esta equivalente a 1 l.
Como 1.000 cm³ equivalem a 1 dm³, temos que 1 dm³ equivale a 1 l.
Como um litro equivale a 1.000 ml, podemos afirmar que 1 cm³ equivale a 1 ml.
1.000 dm³ equivalem a 1 m³, portanto 1 m³ é equivalente a 1.000 l, que equivalem a 1 kl.
Exemplos de Conversão entre Medidas de Volume e Medidas de Capacidade
Quantos decalitros equivalem a 1 m3?
Sabemos que 1 m3 equivale a 1.000 l, portanto para convertermos de litros a decalitros, passaremos um nível à esquerda. Dividiremos então 1.000 por 10 apenas uma vez:
1000 l : 10 = 100 dal
Isto equivale a passar a vírgula uma casa para a esquerda.
Poderíamos também raciocinar da seguinte forma:
Como 1 m3 equivale a 1 kl, basta fazermos a conversão de 1 kl para decalitros, quando então passaremos dois níveis à direita. Multiplicaremos então 1 por 10 duas vezes:
1 kl * 10 * 10 = 100 dal
Portanto:
100 dal equivalem a 1 m3.
348 mm3 equivalem a quantos decilitros?
Como 1 cm3 equivale a 1 ml, é melhor dividirmos 348 mm3 por mil, para obtermos o seu equivalente em centimetros cúbicos: 0,348 cm3. Logo 348 mm3 equivale a 0,348 ml, já que cm3 e ml se equivalem.
Neste ponto já convertemos de uma unidade de medida de volume, para uma unidade de medida de capacidade.
Falta-nos passarmos de mililitros para decilitros, quando então passaremos dois níveis à esquerda. Dividiremos então por 10 duas vezes:
0,348 ml : 10 : 10 = 0,00348 dl
Logo:
348 mm3 equivalem a 0,00348 dl.
Medidas de capacidade
5.1.1 - Transformação de unidades de capacidade
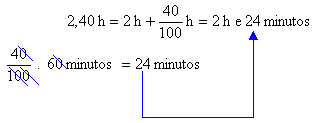
Século – 100 anosMedidas de capacidade
A unidade fundamental para medir capacidade de um sólido é o litro.
De acordo com o Comitê Internacional de Pesos e Medidas, o litro é, aproximadamente, o volume equivalente a um decímetro cúbico, ou seja:
1 litro = 1,000027 dm3
Porém, para todas as aplicações práticas, simples, podemos definir:
1 litro = 1 dm3
Veja os exemplos:
1) Na leitura do hidrômetro de uma casa, verificou-se que o consumo do último mês foi de 36 m3. Quantos litros de água foram consumidos?
Solução: 36 m3 = 36 000 dm3 = 36 000 litros
2) Uma indústria farmacêutica fabrica 1 400 litros de uma vacina que devem ser colocados em ampolas de 35 cm3 cada uma. Quantas ampolas serão obtidas com essa quantidade de vacina?
Solução: 1 400 litros = 1 400 dm3 = 1 400 000 cm3
(1 400 000 cm3) : (35 cm3) = 40 000 ampolas.
(1 400 000 cm3) : (35 cm3) = 40 000 ampolas.
5.1 - Outras unidades para medir a capacidade
São também utilizadas outras unidades para medir capacidade, que são múltiplos e submúltiplos do litro:
Múltiplos
|
u.f.
|
Submúltiplos
| ||||
hectolitro
|
decalitro
|
litro
|
decilitro
|
centilitro
|
mililitro
| |
hl
|
dal
|
l
|
dl
|
cl
|
ml
| |
100 l
|
10 l
|
1 l
|
0,1 l
|
0,01 l
|
0,001 l
| |
Obs. 1) Não é usado nem consta da lei o quilolitro.
Obs. 2) Além do litro, a unidade mais usado é o mililitro (ml), principalmente para medir pequenos volumes, como a quantidade de líquido de uma garrafa, de uma lata ou de uma ampola de injeção.
5.1.1 - Transformação de unidades de capacidade
Observando o quadro das unidades de capacidade, podemos verificar que cada unidade de capacidade é 10 vezes maior que a unidade imediatamente inferior, isto é, as sucessivas unidades variam de 10 em 10.
Veja os exemplos:
1) Expressar 15 l em ml.
Solução: 15 l = (15 x 103) ml = 15 000 ml
2) Expressar 250 ml em cm3.
Solução: 250 ml = 0,25 l = 0,25 dm3 = 250 cm3
Medidas de tempo
A unidade de tempo escolhida como padrão no Sistema Internacional (SI) é o segundo.
Segundo
O Sol foi o primeiro relógio do homem: o intervalo de tempo natural decorrido entre as sucessivas passagens do Sol sobre um dado meridiano dá origem ao dia solar.
O segundo (s) é o tempo equivalente a
|
As medidas de tempo não pertencem ao Sistema Métrico Decimal.
Múltiplos e Submúltiplos do Segundo
Quadro de unidades
Múltiplos
| ||
| minutos | hora | dia |
| min | h | d |
| 60 s | 60 min = 3.600 s | 24 h = 1.440 min = 86.400s |
São submúltiplos do segundo:
- décimo de segundo
- centésimo de segundo
- milésimo de segundo
Cuidado: Nunca escreva 2,40h como forma de representar 2 h 40 min. Pois o sistema de medidas de tempo não é decimal.
Observe:
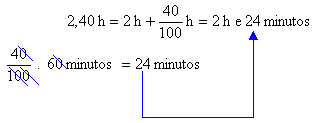
Década – 10 anos
Ano – aproximadamente 365 dias
Mês – 30 e 31 dias
Dia – 24 horas
Hora – 60 minutos
Minuto – 60 segundos
Nenhum comentário:
Postar um comentário