Artigo com questões sobre relações métricas no triângulo retângulo resolvidas e propostas


03. No triângulo retângulo abaixo determinar a hipotenusa, as projeções dos catetos sobre a hipotenusa e a altura relativa a hipotenusa:

Resolução:
Pelo teorema de Pitágoras temos:
x2 = 52 + 122
x2 = 169
x = 13
Aplicando as relações de projeções de catetos, vem:
52 = x . z
13 . z = 25
z = 25 / 13
122 = x . t
13 . t = 144
t = 144 / 13
04. Dado o triângulo retângulo ABC, reto em A, representado na figura abaixo, calcule os valores desconhecidos (x, m, n e h).
x = 4 m,
h = 12/5 m = 2,4 m,
m = 9/5 m = 1,8 m,
n = 16/5 m =3,2 m
h = 12/5 m = 2,4 m,
m = 9/5 m = 1,8 m,
n = 16/5 m =3,2 m
05. Em um triangulo retângulo, sua altura(h) é = 5 e sua hipotenusa(a) é =26. Calcule o cateto b (cateto maior).
Vamos recordar as relações métricas em um triângulo retângulo:
a = m + n
b² = a.m
c² = a.n
b.c = a.h
h² = m.n
a² = b² + c²
no exercício dado, sabemos que
h = 5
a = 26
observe que nenhuma das relações métricas envolve apenas essas duas medidas
vamos ter que encontrar um caminho.
Façamos, primeiro:
m + n = a
m + n = 26
n = 26 - m (I)
b² = a . m (onde m é a maior das projeções)
b² = 26m (II)
c² = a.n
c² = 26n --> c² = 26(26 - m) --> c² = 676 - 26m (III)
b . c = a . h
b . c = 26 . 5
b . c = 130
eleva ao quadrado:
b² c² = 16900
substitui (II) e (III)
26m ( 676 - 26m) = 16900
17576m - 676m² = 16900
676m² - 17576m + 16900 = 0 --> simplifica por 676
m² - 26m + 25 = 0
resolve por báskara ou pela soma e produto:
m' = 25
m" = 1 (despreza por ser o menor)
b² = 26m (II)
b² = 25 . 26 ==> b = 5√26 m que é o cateto maior
como a = m + n
n = 1
c² = 26n --> c² = 26 --> c= √26 m que é o cateto menor
Poderíamos também usar outras duas relações métricas:
h = m.n ---> m . n = 25 (I)
a = m + n --> m + n = 26 donde m = 26 - n (II)
Substitui (II) em (I)
( 26 - n ) . n = 25
n² - 26n + 25 = 0
resolvendo por báskara ou pela soma e produto:
n' = 1
n" = 25 (despreza, pois consideramos inicialmente que m é a maior)
como
m = 26 - n (II)
m = 26 - 1
m = 25
assim, sabendo que
b² = a.m
temos
b² = 26 . 25
b = √ 5² . 26
b = 5 √ 26
logo, o cateto maior b = 5 √26 m
a = m + n
b² = a.m
c² = a.n
b.c = a.h
h² = m.n
a² = b² + c²
no exercício dado, sabemos que
h = 5
a = 26
observe que nenhuma das relações métricas envolve apenas essas duas medidas
vamos ter que encontrar um caminho.
Façamos, primeiro:
m + n = a
m + n = 26
n = 26 - m (I)
b² = a . m (onde m é a maior das projeções)
b² = 26m (II)
c² = a.n
c² = 26n --> c² = 26(26 - m) --> c² = 676 - 26m (III)
b . c = a . h
b . c = 26 . 5
b . c = 130
eleva ao quadrado:
b² c² = 16900
substitui (II) e (III)
26m ( 676 - 26m) = 16900
17576m - 676m² = 16900
676m² - 17576m + 16900 = 0 --> simplifica por 676
m² - 26m + 25 = 0
resolve por báskara ou pela soma e produto:
m' = 25
m" = 1 (despreza por ser o menor)
b² = 26m (II)
b² = 25 . 26 ==> b = 5√26 m que é o cateto maior
como a = m + n
n = 1
c² = 26n --> c² = 26 --> c= √26 m que é o cateto menor
Poderíamos também usar outras duas relações métricas:
h = m.n ---> m . n = 25 (I)
a = m + n --> m + n = 26 donde m = 26 - n (II)
Substitui (II) em (I)
( 26 - n ) . n = 25
n² - 26n + 25 = 0
resolvendo por báskara ou pela soma e produto:
n' = 1
n" = 25 (despreza, pois consideramos inicialmente que m é a maior)
como
m = 26 - n (II)
m = 26 - 1
m = 25
assim, sabendo que
b² = a.m
temos
b² = 26 . 25
b = √ 5² . 26
b = 5 √ 26
logo, o cateto maior b = 5 √26 m


08. No triângulo retângulo abaixo determinar a hipotenusa, as projeções dos catetos sobre a hipotenusa e a altura relativa a hipotenusa:
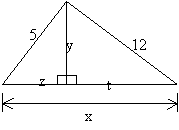
Resolução:
Pelo teorema de Pitágoras temos:
x2 = 52 + 122
x2 = 169
x = 13
Aplicando as relações de projeções de catetos, vem:
52 = x . z
13 . z = 25
z = 25 / 13
122 = x . t
13 . t = 144
t = 144 / 13
Aplicando a relação do produto dos catetos, vem:
x . y = 5 . 12
13 . y = 60
y = 60 / 13
Agora pratique:
09. (FATEC-SP) Se os catetos de um triângulo retângulo T, medem, respectivamente, 12 cm e 5 cm, então a altura de T relativa à hipotenusa é:
a) 12/5 m b) 5/13 m c) 12/13 m d) 25/13 m e) 60/13 m
10. Sabe-se que a altura de um triângulo retângulo mede 48 cm e a medida de um dos catetos é igual a 60 cm. A projeção desse cateto sobre a hipotenusa é:
a) 33 b) 34 c) 35 d) 36 e) 37
a) 33 b) 34 c) 35 d) 36 e) 37
11. (Cesgranrio-RJ) Num triângulo retângulo em A, a altura relativa à hipotenusa mede 12, e o menor dos segmentos que ela determina sobre a hipotenusa, 9. O menor lado do triângulo mede:
a) 12,5 b) 13 c) 15 d) 16 e) 16,5



aiii obrigada !!! vc me salvou !!!
ResponderExcluirA 1 não ta errada não? porque a raiz de 400 é 20 e não 40
ResponderExcluiré realmente é 20 a raiz
Excluira questão 2 também está errada, nao tem como y ser 6, pq será menor que o restante.
ExcluirEste comentário foi removido pelo autor.
Excluira questão 2 está "certa" ele so trocou o lado do y pq o m é o menor lado e não o maior
ExcluirTambém acho,pq 40 é a raiz de 1600.
Excluirsim, tb percebi. provavelmente erro de digitação kk
ExcluirMas de qualquer forma é muito bom o seu site
ResponderExcluira 1 num ta errada n ? affs me confundi mais --'
ResponderExcluirta sim a raiz de 400 é 20
ExcluirA questão 1 tá errada, pois a raiz quadrada de 400 = 20 e não 40. E a questão 11, na divisão de 144 / 9 = 16 e não 15.
ResponderExcluirMas mesmo assim obrigada ajudou bastante.
Sim,mas isso é o valor de N, após fazer a relação métrica de c²=9 x 25= 225( O MENOR LADO DO TRIÂNGULO,QUE É C ), a raiz de 225 irá resultar em 15, esse é o motivo de ser 15. Usa-se a relação métrica de C pelo fato dele ser o menor lado do triângulo retângulo b>c
ExcluirNo exercício 11 não seria ao invés de multiplicar por 9 multiplicar por 16,porque c ao quadrado é igual a vezes n.
Excluira 1 ta errada ou não
ResponderExcluirsim ela ta errada é 20
ExcluirÑ entendi como calcular o quarto :(
ResponderExcluirtudo errado moço, raiz de 400 n é 40
ResponderExcluirblz,a raiz de 400 e 40
ExcluirBlz SOL
ExcluirOloco tio ou! Ó as raiz de 400, meça suas raiz parça!!
ResponderExcluirtroxa asuhaushauhssauh
ExcluirCê éee o Bixão memo en doido
ExcluirSeis e burro é ?? Ate eu sei raiz de 400
ResponderExcluirfoda-se foda-se foda-se foda-se foda-se foda-se foda-se foda-se foda-se foda-se foda-se foda-se foda-se foda-se foda-se foda-se foda-se foda-se foda-se U.u
Excluirraiz de 400 é 20 todo mundo sabe disso seis é muito burro
Excluirkkkkkkk
ResponderExcluirMuito bom o site :)
ResponderExcluirOtario
ExcluirSabe as raiz de 400? Então, meça elas!
ResponderExcluir;)
ResponderExcluirEu acho que é isso ai mesmo.
ResponderExcluirNegethevies
Excluircomo assim parsa raiz de 400 e 40 mer mao, tu tas loiro cachorera, raiz de 400 e 4 mano, flw
ResponderExcluirse for pra falar besteira é melhor ficar calado... A raiz de 400 é 20 pelo amor de Deus...
Excluirblz wesley
ResponderExcluira primeira questao esta errado
ResponderExcluirNossa gente!!! Coitado dele, ele tira tempo pra esse blog e vcs ficam falando mau assim... Todo mundo sabe q ta errada a 1. E ele ja entendeu isso. Não precisam ficar falando tanto. Um comentário já ta de bom tamanho.
ResponderExcluirconcordo porque além do mais todo mundo erra na vida pq errar é humano
ExcluirOlha só a sua explicação foi perfeita parabéns, mas como sabemos nada e perfeito e claro que sempre haverá alguns erros, porém foi bastante útil a sua contribuição para a internet.
ResponderExcluirEssa 3 também tá errada Pq somando 1.9 mais 11.0 da 12.9 e o resultado tem q dar 13
ResponderExcluirCOMO É QUE SE FAZ A QUESTAO 10 ?
ResponderExcluircomo assim vcs colocam a questão mas não mostram o caminho de cada resultado? tipo a 04......??
ResponderExcluirNa sexta questão há seis ( raiz de cinco ) elevado a 2, o seis foi multiplicado por ele mesmo e a raiz foi cortada com o expoente, mas o seis n deveria ter sido multiplicado, ja que está fora do parenteses, o site é otimo, mas se estiver msm errado, melhor consertar!
ResponderExcluirEste comentário foi removido pelo autor.
ResponderExcluira raiz de 400 é 20 não é? a 1 esta incorreta
ResponderExcluirA raiz de 400 é 20... mas tirando isso, seu site é muito bom, parábens
ResponderExcluirA questao 11esta erreda?
ResponderExcluirSó eu que não entendi a primeira parte da letra A da 6? Quero entender o porquê o 6 raiz de 5 é a hipotenusa, se o triângulo retângulo utilizado é o com o ângulo reto cortado.
ResponderExcluirA questão 11 esta correta: o menor dos segmentos que ela determina sobre a hipotenusa, 9 ( nesse caso esta se referindo ao cateto de lado c do triangulo ABC onde 9 é a projeção do cateto c) Então temos um triangulo retângulo de cateto 12 e 9 e o lado c sendo a hipotenusa desse do Triangulo pequeno. e ao mesmo tempo o menor dos lados do triangulo retângulo ABC. 12^2 + 9^2 = c^2 = 144 + 81 = c^2 = 225 = c^2 = c = 15.
ResponderExcluirComo faz a Questão 9 ??
ResponderExcluirthis is a very nice article. we provide all kinds of photo editing service provide from Clipping Expert Asia. Which provide all kinds of photo editing service at a competitive price that ensures to make the product images appealing and eye-catching.
ResponderExcluirhttps://clippingexpertasia.com