Conjuntos Numéricos operações - teoria e exercícios

Teoria, questões e operações com Conjuntos numéricos

Conjunto dos números Inteiros

O conjunto dos números Inteiros é representado pela letra Z (maiúscula), inclui todos os números inteiros positivos e inteiros negativos. Para indicar que o zero não está fazendo parte do conjunto determinado, indicamos assim Z*. Observe os exemplos a seguir:

Z = {.... , -4, -3, -2, -1, 0, 1, 2, 3, 4, ....}
Z* = {.... , -3, -2, -1, 1, 2, 3, ...}

Podemos notar que no conjunto dos números Inteiros todos os elementos possuem antecessores e sucessores.

Podemos considerar os números inteiros ordenados sobre uma reta, conforme mostra o gráfico abaixo:

Operações entre números Inteiros

Adição e subtração

Roberta depositou em sua conta bancária a quantia de R$ 200,00. Ao conferir o saldo de sua conta notou que possuía um valor negativo de R$ -50,00. Quanto Roberta devia ao banco?
Resolução:
Ao depositar R$ 200,00 e continuar devendo R$ 50,00, podemos chegar a conclusão de que Roberta devia ao banco R$ 250,00. Nos bancos os saldos devedores são simbolizados pelo sinal (–).
Podemos realizar a seguinte operação Matemática:
– 250 + 200 = – 50

Na adição e na subtração utilizamos a seguinte definição:
Números com sinais diferentes: subtrai e conserva o sinal do maior.
– 20 + 3 = – 17 + 48 – 18 = + 30

Números com sinais iguais: soma e conserva o sinal.
– 20 – 5 = – 25 + 18 + 3 = + 21

Multiplicação e Divisão
Para realizar a multiplicação e a divisão entre números Inteiros é preciso utilizar o jogo de sinais.
(+) com (+) = +
(–) com (+) = –
(+) com (–) = –
(–) com (–) = +

(+6) * (– 3) = – 18
(–6) * (–8) = +48
(–81) : (–9) = +9
(+100) : (–10) = –10

Conjunto dos números Racionais

Os números racionais é um conjunto que abrange os números inteiros (Z), números decimais finitos (por exemplo, 743,8432) e os números decimais infinitos periódicos (que repete uma sequência de algarismos da parte decimal infinitamente), como “13,090909…”, são também conhecidas como dízimas periódicas.

Os racionais são representados pela letra Q.
Sempre são expressos na forma de fração. O numerador e o denominador desta fração devem pertencer ao conjunto dos números inteiros e obviamente o denominador não poderá ser igual a zero, pois não há divisão por zero.

O número 20,1 por exemplo, pode ser expresso como , assim como 0,375 pode ser expresso como 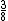 e 0,2 por ser representado por .

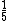Note que se dividirmos quatro por nove, iremos obter 0,44444... que é um número com infinitas casas decimais, todas elas iguais a quatro. Trata-se de uma dízima periódica simples que também pode ser representada como 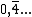, mas que apesar disto também é um número racional, pois pode ser expresso como .

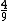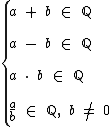
A realização de qualquer uma das quatro operações aritméticas entre dois números racionais quaisquer terá como resultado também um número racional, obviamente no caso da divisão, o divisor deve ser diferente de zero. Sejama e b números racionais, temos:

Conjunto dos números Irracionais

É formado pelos números decimais infinitos não-periódicos. Um bom exemplo de número irracional é o número PI (resultado da divisão do perímetro  de uma circunferência pelo seu diâmetro), que vale 3,14159265 …. Atualmente, supercomputadores já conseguiram calcular bilhões de casas decimais para o PI.
Também são irracionais todas as raízes não exatas, como a raiz quadrada de 2 (1,4142135 …).

A raiz quadrada dos números naturais é uma ótima fonte de números irracionais, de fato a raiz quadrada de qualquer número natural que não seja um quadrado perfeito é um número irracional. 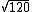 é um número irracional, pois 120 não é um quadrado perfeito, ou seja, não há um número natural que multiplicado por ele mesmo resulte em cento e vinte, já  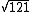é um número natural, pois .

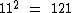A letra I ( 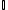 ) representa o conjunto dos número irracionais.

Conjunto dos números Reais

É formado por todos os conjuntos ditos anteriormente(união do conjunto dos racionais com os irracionais). Portanto, os números naturais, inteiros, racionais e irracionais são todos números reais. Como subconjuntos importantes de IR temos:

IR* = IR-{0}

IR₊ = conjunto dos números reais não negativo

IR_ = conjunto dos números reais não positivos

É representado pela letra R.

Conjunto dos números Complexos

Chama-se conjunto dos números complexos, e representa-se por C, o conjunto de pares ordenados, ou seja:

z = (x,y)
onde x pertence a R e y pertence a R.

Então, por definição, se z = (x,y) = (x,0) + (y,0)(0,1) onde i=(0,1), podemos escrever que:

z=(x,y)=x+yi

Exemplos:
(5,3)=5+3i
(2,1)=2+i
(-1,3)=-1+3i ...

Dessa forma, todo o números complexo z=(x,y) pode ser escrito na forma z=x+yi, conhecido como forma algébrica, onde temos:

x=Re(z, parte real de z
y=Im(z), parte imaginária de z

O conjunto dos números complexos, veio pra resolver raízes com índices pares de radicando negativo, pois no conjunto dos reais essa operação não teria solução.
Podemos concluir que o conjunto dos números reais está contido no conjunto dos números complexos.

REPRESENTAÇÃO GRÁFICA DE COMPLEXOS Z(x,y) = Z(nºreal; nºimaginário)
Onde: a coordenada x = um número real
           a coordenada y = um número imaginário  

Exercícios Conjuntos numéricos com Gabarito

1) Num grupo de 61 pessoas 18 gostam de seriados, mas não gostam de telenovelas; 5 pessoas não gostam de telenovelas e nem de seriados; 25% das pessoas que gostam de seriados também gostam de telenovelas.
O total de pessoas do grupo que gostam de telenovelas, mas não gostam de seriados é:

a) 30                                   b) 32                           c) 34                                  d) 36

2) (FATEC) Se x e y são números reais tais que x = (0,25)0,25 e y=16–0,125, é verdade que
a) x = y
b) x > y
c) x·y = 2
d) x - y é um número irracional.
e) x + y é um número racional não inteiro.

3) (EXTRA)  Dado que r é um número racional e Y um número irracional, é verdade que:
(A) x·Y é racional
(B) Y2 é racional
(C) x·Y pode ser racional
(D) x·Y é irracional
(E) x + Y é racional

4) (PUC-RIO) Num colégio de 100 alunos, 80 gostam de sorvete de chocolate, 70 gostam de sorvete de creme e 60 gostam dos dois sabores. Quantos não gostam de nenhum dos dois sabores?
a) 0                             b) 10                  c ) 20                  d) 30                         e) 40

5) (UFF) Segundo o matemático Leopold Kronecker (1823-1891), “Deus fez os números inteiros, o resto é trabalho do homem.” Os conjuntos numéricos são, como afirma o matemático, uma das grandes invenções humanas. Assim, em relação aos elementos desses conjuntos, é correto afirmar que:
A) o produto de dois números irracionais é sempre um número irracional.
B) a soma de dois números irracionais é sempre um número irracional.
C) entre os números reais 3 e 4 existe apenas um número irracional.
D) entre dois números racionais distintos existe pelo menos um número racional.
E) a diferença entre dois números inteiros negativos é sempre um número inteiro negativo.

Veja também:

Dízima Periódica: Questões resolvidas e teoria

Função do 1° grau: teoria e exercícios vestibular

Função do 2º grau: teoria e exercícios vestibular

Questões de provas Banco do Brasil escriturário (matemática)

kit domínio + hospedagem        

Guia de Estratégias é um livro digital sobre estratégias e técnicas de estudo.

Desenvolva as habilidades necessárias para conquistar um cargo público.

Tópicos abordados no livro (capítulos):

• Fique motivado.
• Estabeleça metas.
• Desenvolva a sua memória.
• Controle o seu tempo.
• Faça anotações.
• Crie mapas mentais.
• Aprenda leitura dinâmica.
• Organize o seu ambiente de estudos.
• Prepare-se para o dia da prova.

Garanta agora o seu exemplar digital! De 47,00 por 19,90

 site:     http://www.concursopublicofacil.com.br/?ref=A142611c