Exercícios Arranjos simples
Resolução:
Sabemos que 1 ano é composto de 12 meses, então devemos determinar o número de sequência através do arranjo de 12, tomados 6 a 6.

02. Em uma urna de sorteio de prêmios existem dez bolas enumeradas de 0 a 9. Determine o número de possibilidades existentes num sorteio cujo prêmio é formado por uma sequência de 6 algarismos.
Resolução:

03. Em uma escola está sendo realizado um torneio de futebol de salão, no qual dez times estão participando. Quantos jogos podem ser realizados entre os times participantes em turno e returno?
Resolução:
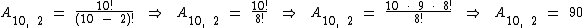
04. . Calcule o número de arranjos simples de 10 elementos tomados 3 a 3.

03. Em uma escola está sendo realizado um torneio de futebol de salão, no qual dez times estão participando. Quantos jogos podem ser realizados entre os times participantes em turno e returno?
Resolução:
Como o campeonato possui dois turnos, os jogos Equipe A x Equipe B e Equipe B x Equipe A tratam-se de partidas distintas, então estamos trabalhando com arranjos simples onde importa a ordem dos elementos. Devemos calcular A10, 2:
04. . Calcule o número de arranjos simples de 10 elementos tomados 3 a 3.
05. Calcule:
a) A6,4 b )A5,3 c) A15,2 d) A4,1
a) 551 b) 552 c) 553 d) 554 e) 555
07. Com os algarismos 1, 2, 3, 4, 5, 6 e 7, quantos números de 4 algarismos distintos podemos escrever?
08.(OSEC-SP) Uma faculdade mantém 8 cursos diferentes. No vestibular, os candidatos podem fazer opção por 3 cursos, determinando-os por ordem de preferência. Então, o número de posível de formas de optar é:
a) 6.720 b) 336 c) 520 d) 120 e) 56
Gabarito:
01) 665.280 2) 151. 200 3) 90 4) 720 5) a) 360 b) 60 c) 210 d) 4 6) A 7) 720 8) B
resposta da 7 ta onde
ResponderExcluirantes da resposta da oito
ExcluirVamos analizar a 7° Questão pelo princípio fundamental de contagem.
ExcluirA mesma pede 4 algarismos distintos, e o elemento A é 7, logo:
A7, 4= 7!/(7-4)! => 7!/3! => 7.6.5.4.3! /3!
anulamos os " 3! " e adiante encontramos: 7.6.5.4= 840 <------Resposta
Obs:O erro foi dado pela resposta do autor em relação a essa questão, por esse motivo vc entrou em contradição com a resposta. Boa Noite :)
Ufa !
Excluirqueria o cálculo da 6ª e da 7ª
ResponderExcluirnao sei
Excluir6 Questão.
ExcluirR:
5.5.5.5= 625
ela não quer forma o número 13, logo:
_._ 13 _13_ 13_._ então: 3.5.5= 75
Obs:Mas ainda temos a possíbilidade de senha 13 13 que já está incluída nos 75, então:
Fica: 625-75-1= 551 <----------Resposta
Boa Noite
7) 7x6x5x4=840
ExcluirEste comentário foi removido pelo autor.
Excluiró asideia
ResponderExcluirO raciocínio está corretíssimo,mas resultaria em 549 pelas contas apresentadas.Aí ,a questão teria que ser anulada,a não ser que ,ao invés de subtrair tivermos que somar !
ResponderExcluirSe ele subtraiu o 1313 duas vezes então tem q somar 1 à resposta final. Ou seja: 550 + 1 = 551
Excluirn entendi a 6 e 7 alguem mim ajuda aee pfff
ResponderExcluirMeu nome é jose Antônio e eu estou precisando muito saber como eu resolvo essa qüestão: Considerando os algarismos 1,2,3,4,5,6,7,8responda:Quantos números de 4 algarismos podemos formar? Quantos números de 4 algarismos distintos podemos formar? Quantos números pares de 4 algarismos podemos formar? Me ajudem minha prova é amanhã dia 16-11-2016.se possível me mande a fórmula para cada qüestão. Obrigado
ResponderExcluirEste comentário foi removido pelo autor.
ResponderExcluirInferno, perdi meu tempo na sétima questão pq a resposta ta errada. É oitocentos e quarenta não setecentos e vinte😠
ResponderExcluirObrigado!!!!!!!!!!!!
ResponderExcluir