Em física, uma onda é uma perturbação oscilante de alguma grandeza física no espaço e periódica no tempo. A oscilação espacial é caracterizada pelo comprimento de onda e o tempo decorrido para uma oscilação é medido pelo período da onda, que é o inverso da sua frequência. Estas duas grandezas estão relacionadas pela velocidade de propagação da onda.
Fisicamente, uma onda é um pulso energético que se propaga através do espaço ou através de um meio (líquido, sólido ou gasoso). Segundo alguns estudiosos e até agora observado, nada impede que uma onda magnética se propague no vácuo ou através da matéria, como é o caso das ondas eletromagnéticas no vácuo ou dos neutrinos através da matéria, onde as partículas do meio oscilam à volta de um ponto médio mas não se deslocam.
Quanto a natureza podemos então dividir as ondas em dois tipos:
- Ondas mecânicas: são todas as ondas que precisam de um meio material para se propagar.
Ex: ondas no mar, ondas sonoras, ondas em uma corda, etc.
- Ondas eletromagnéticas: são ondas que não precisam de um meio material para se propagar. Elas também podem se propagar em meios materiais. Exemplos: luz, raio-x , sinais de rádio, etc.
Ex: As ondas luminosas são ondas eletromagnéticas.
Quanto a direção de propagação as ondas podem ser:
- Ondas longitudinais: são as ondas onde a vibração da fonte é paralela ao deslocamento da onda.
Ex: As ondas sonoras são ondas mecânicas do tipo longitudinal.
- Ondas transversais: a vibração é perpendicular à propagação da onda.
Ex: ondas eletromagnéticas, ondas em uma corda (você balança a mão para cima e para baixo para gerar as ondas na corda).
Características das ondas
Todas as ondas possuem algumas grandezas físicas, que são:
Todas as ondas possuem algumas grandezas físicas, que são:
- Comprimento de onda
- Frequência
- Amplitude
- Período
- Velocidade de propagação
- Comprimento de onda: é o tamanho de uma onda, que pode ser medida em três pontos diferentes: de crista a crista, do início ao final de um período ou de vale a vale. Crista é a parte alta da onda, vale, a parte baixa. É representada no SI pela letra grega lambda (λ)
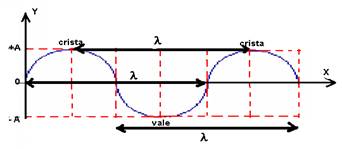
- Frequência: é o número de oscilações da onda, por um certo período de tempo. A unidade de frequência do Sistema Internacional (SI), é o hertz (Hz), que equivale a 1 segundo, e é representada pela letra f. Então, quando dizemos que uma onda vibra a 60Hz, significa que ela oscila 60 vezes por segundo. A frequência de uma onda só muda quando houver alterações na fonte.
-Período: É o tempo que a onda demora para percorrer um comprimento de onda (1 l), que é o mesmo tempo que um ponto qualquer da onda demora para oscilação (vai e vem) completa e que é o mesmo tempo que a fonte demora para gerar uma onda completa. No SI, é representado pela letra T, e é medido em segundos.
É possível criar uma equação relacionando a frequência e o período de uma onda:

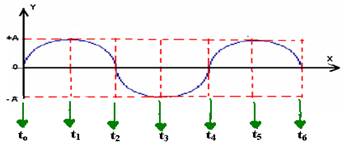
Na figura acima, o período T é o tempo compreendido entre os instantes T=t4-to=t5-t1=t6-t2, etc.
- Velocidade: A velocidade de propagação de uma onda é a rapidez com que a onda se propaga em determinado meio. Depende da distância percorrida pela onda e também do intervalo de tempo gasto para percorrer essa distância.
Para calcular a velocidade de propagação de uma onda, pode utilizar-se a expressão seguinte:

Sendo:
c = velocidade de propagação (m/s)
l= comprimento de onda (m)
u = frequência (Hz)
|
- Amplitude: A amplitude (A) representa o máximo afastamento, durante a oscilação, em relação à posição de equilíbrio. Na figura ao lado, a posição de equilíbrio está representada pela linha tracejada.

Velocidade de propagação dos pulsos nos meios unidimensionais
- Denominamos de densidade linear (m) de uma corda homogênea, de seção transversal constante, que possui massa (m) e comprimento (l), à expressão:
m = m/l
- Significado físico de m --- significa quanto de massa a corda tem por unidade de comprimento. Assim, uma corda de 0,5kg/m possui, no SI, 0,5kg de massa para cada 1 metro de comprimento.
- A velocidade (V) de propagação do pulso na corda é dada por:

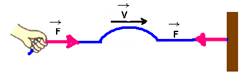
Onde F é a intensidade da força que traciona (estica) a corda.
Observe que V é diretamente proporcional a ÖF, ou seja, quanto mais esticada estiver a corda, maior será a velocidade de propagação do pulso ou da onda na mesma e que V é inversamente proporcional a Öm, ou seja, quanto maior a densidade linear da corda, menor será a velocidade de propagação da onda na mesma.
Os fenômenos ondulatórios.
Vamos lá:
Reflexão
A reflexão ondulatória é a mesma da reflexão da óptica geométrica. Há apenas uma análise diferenciada para alguns casos.
Ângulo de incidência = ângulo de reflexão.

Na reflexão pode ocorrer apenas mudança de direção. As outras grandezas se mantêm.
Reflexão em cordas.
Pode ocorrer com uma corda fixa a uma parede ou livre para oscilar. Ao produzir um pulso na corda, os pontos vibram para cima e para baixo. Desse modo o pulso tenta levantar e abaixar a corda. Quando o pulso alcança a extremidade podemos ter duas situaçoes:
Na corda fixa há a inversão de fase, pois a parede oferece resistência ao pulso que se propaga e tenta "levantar" a parede. A parede exerce uma força contrária (ação e reação) e o pulso volta invertido.
Na corda livre não há inversão de fase, o pulso retorna do mesmo modo, pois a parte livre não oferece resistência.

Obs.: A reflexão sonora ocorre como qualquer onda. Contudo, o ouvido humano só reconhece sons distintos quando há um intervalo superior a 0,1 segundo entre esses sons. Quando o som emitido retorna ao emissor em um intervalo praticamente nulo é chamado reforço. Quando retorna em um intervalo entre 0 e 0,1 s é a chamada reverberação. Quando retorna após 0,1 essa reflexão é chamada de eco.
Refração
O fenômeno é caracterizado pela mudança na velocidade da onda. Possui a mesma estrutura da refração da óptica geométrica, com mais alguns detalhes.
- Não há variação de frequencia ou período para uma onda que sofre refração. O comprimento de onda é que varia de forma diretamente proporcional à velocidade.
- Não é preciso mudança de direção ou de meio para que ocorra refração. É preciso que ocorram mudanças nas características do meio para que a velocidade modifique. Por exemplo, para uma onda do mar basta mudar a profundidade que teremos mudança de velocidade, para uma onda sonora a velocidade no ar quente é diferente do ar frio.
Refração em superfície

O desenho anterior ilustra ondas do mar vistas de cima que atingem um banco de areia (redução de velocidade).
Refração em cordas
A mudança de velocidade de uma onda em uma corda ocorre quando há cordas de densidades lineares diferentes.
Observe um pulso que se propaga de uma corda grossa para uma corda fina.
Na corda fina o pulso refratado terá maior velocidade e maior comprimento de onda. Observe que há também o surgimento de um pulso refletido que retorna na mesma fase (a corda fina não oferece resistência, funciona como reflexão de corda livre).
Observe um pulso que se propaga de uma corda fina para uma corda grossa.
Na corda fina o pulso refratado terá menor velocidade e menor comprimento de onda. Observe que há também o surgimento de um pulso refletido que retorna na fase oposta (a corda grossa oferece resistência, funciona como reflexão de corda fixa).

A Lei de Snell também é valida, sendo seu uso através da relação de velocidade mais comum. Na óptica seu uso comum é com o índice de refração

Difração
A onda contorna um obstáculo (ou abertura). Só ocorre quando o comprimento de onda tem dimensões próximas do obstáculo (ou abertura).

Obs.: O comprimento de onda sonora fica entre 1,7 cm e 17 m, por isso a onda sonora controna facilmente objetos do nosso cotidiano como uma porta, janela, muro e coisas cujas dimensões variem próximas do comprimento de onda. Para a luz o comprimento de onda é muito pequeno (valores por volta de 0,0000001 m = 10-7 m), assim para observar a luz fazendo curva é preciso um obstáculo muito pequeno.
Interferência
A interferência é o resultado da superposição entre ondas. Pode provocar um aumento na amplitude (interferência construtiva) ou diminuição na amplitude (interferência destrutiva).
Interferência em cordas:
Fases iguais: as amplitudes se somam.
Fases opostas: as amplitudes se subtraem

Interferência em superfície.
Imagine uma fonte vibrando na superfície de um lago. Serão produzidas ondas circulares representadas por suas cristas no desenho a seguir.

Agora imagine duas fontes (F1 e F2) produzindo ondas iguais.

Os pontos indicados representam interferências construtivas e destrutivas.
Polarização
A onda é forçada a se propagar em um único plano. Só ocorre com ondas transversais.
Pense em uma pessoa sacudindo uma corda presa em uma parede em um movimento circular.

Agora imagine que há uma fresta entre a pessoa e a parede. Do lado da pessoa a corda ficará girando, mas do outro lado da fresta, a corda só poderá subir e descer. Assim será criada uma onda transversal que se propaga apenas na direção da fresta.

O desenho a seguir ilustra uma onda que foi criada a partir de um movimento rotatório. Ao passar pela primeira fenda a onda só oscila na horizontal. Ao atravessar a fenda vertical a onda é nula, pois não há movimento vertical.

Obs.: Uma onda luminosa que atravessa um polarizado ficará com apenas uma direção de propagação. Se outro polarizador for colocado de maneira transversal ao primeiro, a onda luminosa não atravessará, ficando a região comum entre os polarizadores sem luz. Girando um dos polarizadores, a área comum escurece. Girando 90o não passa luz

Questões resolvidas Ondulatória (Ondas)
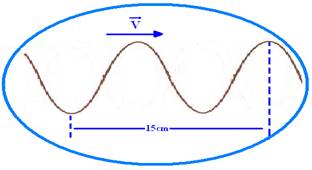
horizontal. A freqüência da onda é f = 740 Hz.
Calcule a velocidade de propagação da onda, em m/s.
2) (IFNMG-MG-012) Algumas aranhas, valendo-se da tensão superficial, podem caminhar sobre a superfície livre da água. Para atrair eventuais presas, a aranha produz pequenas vibrações, gerando ondas superficiais, as quais apresentam comprimento de
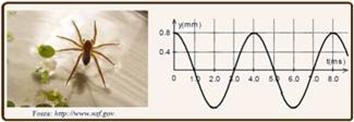
onda igual a 2,0 mm. O deslocamento vertical das partículas de água varia com o tempo (dado em milissegundos, ms) conforme o gráfico apresentado na figura seguinte.
Nessas condições, o valor da velocidade de propagação de tais ondas, expresso em cm/s, está corretamente apresentado na alternativa:
A) 80 B) 50 C) 32 D) 16
3) (UNICAMP-SP) O diagnóstico precoce de doenças graves, como o câncer, aumenta de maneira significativa a chance de cura ou controle da doença. A tomografia de Ressonância Magnética Nuclear é uma técnica de diagnostico médico que utiliza imagens obtidas a partir da absorção de radiofreqüência pelos prótons do hidrogênio submetidos a um campo magnético. A condição necessária para que a absorção ocorra, chamada condição de ressonância, é dada pela equação f =lB, sendo f a frequência da radiação, B o campo magnético na posição do próton, e ¸l= 42 MHz/T
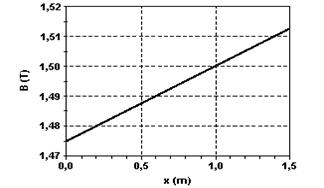
Para se mapear diferentes partes do corpo, o campo magnético aplicado varia com a posição ao longo do corpo do paciente.
a) Observa-se que a radiação de freqüência igual a 63MHz é absorvida quando um paciente é submetido a um campo magnético que varia conforme o gráfico acima. Em que posição x do corpo do paciente esta absorção ocorre?
b) O comprimento de onda é a distância percorrida pela onda durante o tempo de um período. O período é igual ao inverso da freqüência da onda. Qual é o comprimento de onda da radiofreqüência de 63 MHz no ar, sabendo-se que sua velocidade é igual a 3,0 . 108 m/s?
4) (CPS-011) Na Copa do Mundo de 2010, a Fifa determinou que nenhum atleta poderia participar sem ter feito uma minuciosa avaliação cardiológica prévia. Um dos testes a ser realizado, no exame ergométrico, era o eletrocardiograma. Nele é feito o registro da variação dos potenciais elétricos gerados pela atividade do coração.
Considere a figura que representa parte do eletrocardiograma de um determinado atleta.
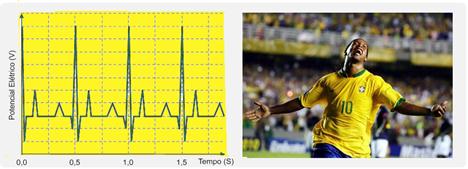
Sabendo que o pico máximo representa a fase final da diástole, conclui-se que a frequência cardíaca desse atleta é, em batimentos por minuto,
a) 60. b) 80. c) 100. d) 120. e) 140.
5) A sirene de uma fábrica produz sons com frequência igual a 2640 Hz.
Determine o comprimento de onda do som produzido pela sirene em um dia cuja velocidade de propagação das ondas sonoras no ar seja igual a 1.188 km/h.
6) (UFAL) Uma onda produzida numa corda se propaga com freqüência de 25 Hz. O gráfico a seguir representa a corda num dado instante.
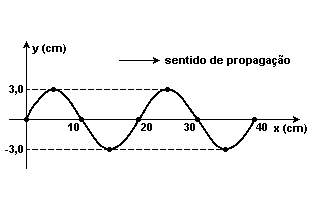
Considere a situação apresentada e os dados do gráfico para analisar as afirmações que seguem.
( ) O período de propagação da onda na corda é 20 s.
( ) A amplitude da onda estabelecida na corda é de 6,0cm.
( ) A velocidade de propagação da onda na corda é de 5,0 m/s.
( ) A onda que se estabeleceu na corda é do tipo transversal.
( ) A onda que se estabeleceu na corda tem comprimento de onda de 10 cm.
7) (UNESP-SP) A sucessão de pulsos representada na figura foi produzida em 1,5s. Determine a freqüência e o período da onda.
8) (UFRJ-RJ) Uma perturbação periódica em uma corda produz ondas de freqüência 40 Hz e comprimento de onda 15 cm.
Neste caso, calcule:
a) o período da onda.
b) a velocidade da onda.
9) (UFMG) Daniel brinca produzindo ondas ao bater com uma varinha na superfície de um lago. A varinha toca a água a cada 5 segundos. Se Daniel passar a bater a varinha na água a cada 3 segundos, as ondas produzidas terão maior:
a) comprimento de onda.
b) freqüência.
c) período.
d) velocidade
10) (Fuvest-SP) Radiações, como raios X, luz verde, luz ultravioleta, microondas ou ondas de rádio, são caracterizadas por seu comprimento de onda (l) e por sua freqüência (f). Quando essas radiações propagam-se no vácuo, todas apresentam o mesmo valor para:
a) 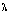 .
.
b) f.
c) V=l.f
b) f.
c) V=l.f
d) l/f
e) 2l/f
11) (UFPE) A figura a seguir mostra esquematicamente as ondas na superfície d'água de um lago, produzidas por uma fonte de freqüência 6,0 Hz, localizada no ponto A.
As linhas cheias correspondem às cristas, e as pontilhadas representam os vales em um certo instante de tempo. Qual o intervalo de tempo, em segundos, para que uma frente de onda percorra a distância da fonte até o ponto B, distante 60 cm?
12) (PUC-SP) Em dezembro de 2004 um terremoto no fundo do oceano, próximo à costa oeste da ilha de Sumatra, foi a perturbação necessária para a geração de uma onda gigante, uma "tsunami". A onda arrasou várias ilhas e localidades costeiras na Índia, no Sri Lanka, na Indonésia, na Malásia, na Tailândia, dentre outras.
Uma "tsunami" de comprimento de onda 150 quilômetros pode se deslocar com velocidade de 750 km/h. Quando a profundidade das águas é grande, a amplitude da onda não atinge mais do que 1 metro, de maneira que um barco nessa região praticamente não percebe a passagem da onda.
Quanto tempo demora para um comprimento de onda dessa "tsunami" passar pelo barco?
a) 0,5 min b) 2 min c) 12 min d) 30 min e) 60 min
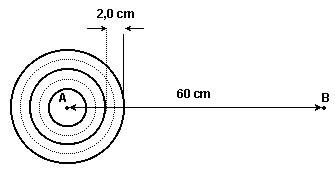
13) (UNESP-SP) A propagação de uma onda no mar da esquerda para a direita é registrada em intervalos de 0,5 s e apresentada através da seqüência dos gráficos da figura, tomados dentro de um mesmo ciclo
Analisando os gráficos, podemos afirmar que a velocidade da onda, em m/s, é de
a) 1,5. b) 2,0. c) 4,0. d) 4,5. e) 5,0.
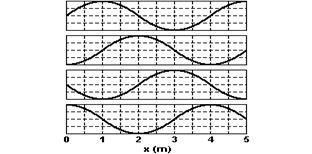
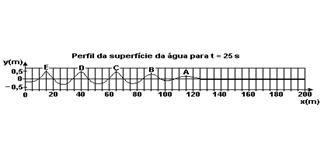
14) (FUVEST-SP) A propagação de ondas na água é estudada em grandes tanques, com detectores e softwares apropriados. Em uma das extremidades de um tanque (Figura 1), de 200 m de comprimento, um dispositivo D produz ondas na água, sendo que o perfil da superfície da água, ao longo de toda a extensão do tanque, é registrado por detectores em instantes subseqüentes. Um conjunto de ondas, produzidas com freqüência constante, tem seu deslocamento y, em FUNÇÃO DO TEMPO, representado na Figura 1, tal como registrado por detectores fixos na posição x = 15 m.
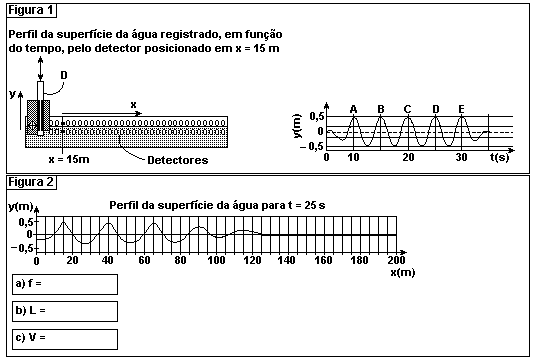
Para esse mesmo conjunto de ondas, os resultados das medidas de sua propagação ao longo do tanque são apresentados a seguir. Esses resultados correspondem aos deslocamentos y do nível da água em relação ao nível de equilíbrio (y = 0).
medidos no instante t = 25 s para diversos valores de x. A partir desses resultados:
a) Estime a freqüência f, em Hz, com que as ondas foram produzidas.
b) Estime o comprimento de onda L, em metros, das ondas formadas.
c) Estime a velocidade V, em m/s, de propagação das ondas no tanque.
d) Identifique, no gráfico da Figura 2 (t = 25 s), as posições das ondas A, B, C, D e E, assinaladas na Figura 1, ainda que, como pode ser observado, as amplitudes dessas ondas diminuam com sua propagação.
15) (UECE) Fornos de micro-ondas usam ondas de rádio de comprimento de onda aproximadamente 12 cm para aquecer os alimentos.

Considerando a velocidade da luz igual a 300 000 km/s a frequência das ondas utilizadas é
a) 360 Hz. b) 250 kHz. c) 3,6 MHz. d) 2,5 GHz.
16) Uma fila de carros, igualmente espaçados, de tamanhos e massas iguais faz a travessia de uma ponte com velocidades iguais e constantes, conforme mostra a figura abaixo. Cada vez que um carro entra na ponte, o impacto de seu peso provoca nela uma perturbação em forma de um pulso de onda. Esse pulso se propaga com velocidade de módulo 10 m/s no sentido de A para B. Como resultado, a ponte oscila, formando uma onda estacionária com 3 ventres e 4 nós.
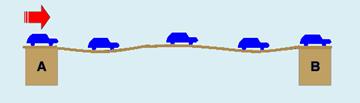
Considerando que o fluxo de carros produza na ponte uma oscilação de 1 Hz, assinale a alternativa correta para o comprimento da ponte.
a) 10 m. b) 15 m. c) 20 m. d) 30 m. e) 45 m.
17) (COLÉGIO NAVAL-011-012) Analise a figura a seguir.
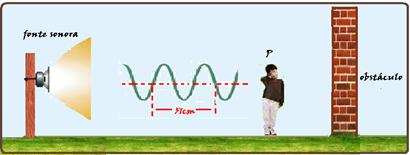
Uma pessoa encontra-se parada em um ponto P, distante de um obstáculo e de uma fonte sonora que emite ondas conforme a configuração mostrada na figura acima. Um som emitido pela fonte no instante to = Os passa pelo ponto P no instante t1 = 0,5 s e retorna ao ouvido da pessoa no instante t2 =2,5s, após ter colidido com o obstáculo. Considerando a velocidade do som no ar como sendo constante e igual a 340m/ s, é correto afirmar que o comprimento de onda, a frequência da fonte emissora e a distância da pessoa até o obstáculo valem, respectivamente:
(A) λ=0,17m; f =1000Hz; d = 170m (B) λ = 0,34m; f =1000Hz; d=340m. (C) λ =0,34m; f=2000Hz; d=170m (D) λ =0,51m; f=1000Hz; d=340m (E) λ =0, 51m; f =2000Hz; d=680m
18) (UNIFESP-SP) O gráfico representa a profundidade (y) no mar em função da velocidade do som (v). A freqüência do som é de 3000 Hz; essa curva é válida para condições determinadas de pressão e salinidade da água do mar.
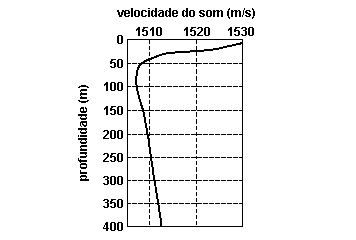
a) Nessas condições, faça uma avaliação aproximada do valor mínimo atingido pela velocidade do som no mar e da profundidade em que isso ocorre.
b) Desenhe na folha de respostas o esboço do correspondente gráfico profundidade (y) em função do comprimento de onda (—) do som. Adote o mesmo eixo e a mesma escala para a profundidade e coloque o comprimento de onda no eixo das abscissas. Represente três valores de —, escritos com três algarismos significativos.
19) Uma agulha vibratória produz ondas com velocidade de propagação igual a 160m/s e comprimento de onda de 1mm, chegando em uma diferença de profundidade com um ângulo formado de 45° e sendo refratado. Após a mudança de profundidades o ângulo refratado passa a ser de 30°. Qual é a nova velocidade de progação da onda?
21) A figura mostra dois pulsos idênticos em comprimento e amplitude e com fases distintas que se propagam em uma corda.

19) Uma agulha vibratória produz ondas com velocidade de propagação igual a 160m/s e comprimento de onda de 1mm, chegando em uma diferença de profundidade com um ângulo formado de 45° e sendo refratado. Após a mudança de profundidades o ângulo refratado passa a ser de 30°. Qual é a nova velocidade de progação da onda?
E o comprimento das ondas refratadas?
Reflexão
20) Uma pessoa emite um som em frente a um anteparo. Após um intervalo de 0,1 s o som retorna ao emissor. Considere a velocidade do som no ar como 340 m/s. A distância entre a pessoa e o anteparo é:
a) 1,7 m b) 3,4 m c) 17 m d) 34 m e) 170 m
21) A figura mostra dois pulsos idênticos em comprimento e amplitude e com fases distintas que se propagam em uma corda.

Após um certo instante ocorre a total superposição dos pulsos.
Podemos afirmar que:

a) as velocidades dos pontos A e B da corda são nulas.
b) a velocidade do ponto B da corda é vertical para baixo.
c) a velocidade do ponto A da corda é nula.
d) a velocidade do ponto B da corda é nula.
e) a velocidade do ponto A da corda é vertical para baixo.
22) O gráfico abaixo representa uma onda que se propaga com velocidade igual a 300m/s.
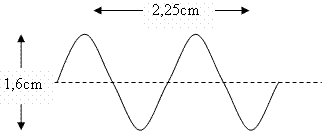

a) o comprimento de onda
b) a freqüência
c) o período
d) a velocidade de propagação
e) a amplitude.
22) O gráfico abaixo representa uma onda que se propaga com velocidade igual a 300m/s.
Determine:
a) a amplitude da onda;
b) o comprimento de onda;
c) a frequência;
d) o período;
23) Um trem de ondas propaga-se ao longo de uma corda tensa. A figura a seguir representa a corda 8,0 segundos após o início do movimento. Determine, para essas ondas:

a) o comprimento de onda
b) a freqüência
c) o período
d) a velocidade de propagação
e) a amplitude.
24) (UFMG) Enquanto brinca, Gabriela produz uma onda transversal em uma corda esticada. Em certo instante, parte dessa corda tem a forma mostrada na figura a seguir.
A direção de propagação da onda na corda também está indicada na figura.
Assinale a alternativa em que estão representados CORRETAMENTE a direção e o sentido do deslocamento do ponto P da corda, no instante mostrado.

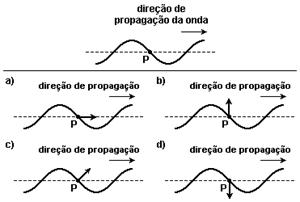
25) (UFRJ) A figura representa a fotografia, em um determinado instante, de uma corda na qual se propaga um pulso assimétrico para a direita. Seja tA o intervalo de tempo necessário para que o ponto A da corda retorne à sua posição horizontal de equilíbrio; seja tB o intervalo de tempo necessário para que o ponto B da corda retorne à sua posição horizontal de equilíbrio. Tendo em conta as distância indicadas na figura, calcule a razão tA/tB.
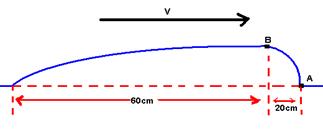
26) (UFCE) A figura a seguir representa uma corda harmônica que se propaga, para a direita, em uma corda homogênea. No instante representado1, 2, 3, 4 e 5.
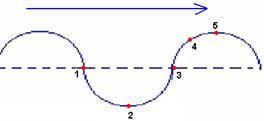
Assinale a alternativa correta:
a) os pontos 1 e 3 tem velocidade nula b) os pontos 2 e 5 tem velocidade máxima
c) o ponto 4 tem velocidade maior que o ponto 1 d) o ponto 2 tem velocidade maior que o ponto 3 e) os pontos 1 e 3 tem velocidade máxima
27) (UEPB-PB-012) O SONAR (sound navigation and ranging) é um dispositivo que, instalado em navios e submarinos, permite medir profundidades oceânicas e detectar a presença de obstáculos. Originalmente foi desenvolvido com finalidades bélicas durante a Segunda Guerra Mundial (1939- 1945). para permitir a localização de submarinos e outras embarcações do inimigo, O seu princípio é bastante simples, encontrando-se ilustrado na figura abaixo.
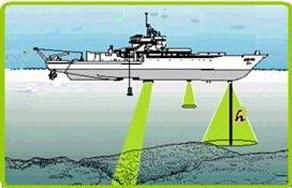
lnicialmente é emitido um impulso sonoro por um dispositivo instalado no navio, A sua frequência dominante é
normalmente de 10 kHz a 40kHz. O sinal sonoro propaga-se na água em todas as direções até encontrar um obstáculo. O sinal sonoro é então refletido (eco) dirigindo-se uma parte da energia de volta para o navio onde é detectado por um hidrofone. (Adaptado dc JUNIOR, F.R. Os Fundamentos da Física. 8. ed. vol. 2. SIo Paulo: Moderna, 2003. p. 417)
Acerca do assunto tratado no texto analise a seguinte situação-problema:
Um submarino é equipado com um aparelho denominado sonar, que emite ondas sonoras de frequéncia 4.0.l04 Hz. A velocidade de propagação do som na água é de l,60.103m/s. Esse submarino, quando em repouso na superfície, emite um sinal na direção vertical através do oceano e o eco é recebido após 0,80s. A profundidade do oceano nesse local e o comprimento de ondas do som na água. em metros, são, respectivamente:
a) 640 e 4.10-2 b) 620 e 4.10-2 c) 630 e 4,5.10-2 d) 610 e 3,5.10-2 e) 600 e 3.10-2
28) (FGV-SP-012) Analise as afirmações.
I. Massa, carga elétrica, temperatura e densidade são algumas das várias grandezas físicas escalares que dispensam as noções de direção e sentido.
II. Campos gravitacional, elétrico e magnético são grandezas vetoriais que caracterizam determinada propriedade física dos pontos de uma região.
III. O estudo das ondas em Física pode ser feito dispensando a aplicação de grandezas vetoriais.
É correto apenas o que se afirma em
(A) I. (B) II. (C) I e II. (D) I e III. (E) II e III.
29) (UFSM-RS-012) A presença e a abrangência dos meios de comunicação na sociedade contemporânea vêm introduzindo elementos novos na relação entre as pessoas e entre elas e o seu contexto.
Radio, televisão e telefone celular são meios de comunicação que utilizam ondas eletromagnéticas, as quais tem a(s) seguinte(s) propriedade(s):
I - propagação no vácuo.
II - existência de campos elétricos variáveis perpendiculares a campos magnéticos variáveis.
III - transporte de energia e não de matéria.
Esta(ao) correta(s):
a) apenas I. b) apenas II. c) apenas III. d) apenas I e II. e) I, II e III.
30) (UNEMAT-MT-012) No passado, durante uma tempestade, as pessoas costumavam dizer que um raio havia caído distante, se o trovão correspondente fosse ouvido muito tempo depois; ou que teria caído perto, caso acontecesse o contrario.
Do ponto de vista da Física, essa afirmação está fundamentada no fato de, no ar, a velocidade do som:
a. variar como uma função da velocidade da luz. b. ser muito maior que a da luz.
c. ser a mesma que a da luz. d. variar com o inverso do quadrado da distancia.
e. ser muito menor que a da luz.
31) (UEPG/2011) No que se refere aos fenômenos ondulatórios, assinale o que for correto:
01) Ao passar de um meio para outro uma onda tem sua frequência alterada.
02) Quando uma onda se reflete em uma barreira, o ângulo de incidência é igual ao ângulo de reflexão.
04) Em uma onda transversal, os pontos do meio em que ela se propaga vibram perpendicularmente à direção de sua propagação.
08) A velocidade de propagação de uma onda depende do meio em que ela se propaga.
32) (UFRGS/2010) A figura abaixo representa dois pulsos produzidos nas extremidades opostas de uma corda.

Assinale a alternativa que melhor representa a situação da corda após o encontro dos dois pulsos:

33) (UFRGS/2010) Considere as seguintes afirmações sobre os fenômenos ondulatórios e suas características:
II. A interferência ocorre apenas com ondas eletromagnéticas.
III. A polarização ocorre apenas com ondas transversais.
Quais estão corretas?
a) Apenas I
b) Apenas II
c) Apenas III
d) Apenas I e II
e) I, II e III.
b) Apenas II
c) Apenas III
d) Apenas I e II
e) I, II e III.
34) Som mais agudo é som de:
a) maior intensidade
b) menor intensidade
c) menor freqüência
d) maior freqüência
e) maior velocidade de propagação.
35) (UFRGS) Quais as características das ondas sonoras que determinam a altura e a
intensidade do som?
a) comprimento de onda e freqüência
b) amplitude e comprimento de onda
c) amplitude e freqüência
d) freqüência e comprimento de onda
e) freqüência e amplitude
36) (Fuvest – SP) Um forno de micro-ondas é projetado para, mediante um processo de ressonância, transferir energia para os alimentos que necessitamos aquecer ou cozer. Nesse processo de ressonância, as moléculas de água do alimento começam a vibrar, produzindo o calor necessário para o cozimento ou aquecimento. A frequência de ondas produzidas pelo forno é da ordem de 2,45.109 Hz, que é igual à frequência própria de vibração da molécula de água.
36) (Fuvest – SP) Um forno de micro-ondas é projetado para, mediante um processo de ressonância, transferir energia para os alimentos que necessitamos aquecer ou cozer. Nesse processo de ressonância, as moléculas de água do alimento começam a vibrar, produzindo o calor necessário para o cozimento ou aquecimento. A frequência de ondas produzidas pelo forno é da ordem de 2,45.109 Hz, que é igual à frequência própria de vibração da molécula de água.
a) Qual o comprimento das ondas do forno?
b) Por que os fabricantes de forno micro-ondas aconselham aos usuários a não utilizarem invólucros metálicos para envolver os alimentos?
37) Por qual motivo as ondas eletromagnéticas limítrofes receberam os nomes: infravermelho e ultravioleta, quando estão na faixa de luz visível?
38) (PUC - RS) Em 1895, o físico alemão Wilheim Conrad Roentgen descobriu os raios X, que são usados principalmente na área médica e industrial. Esses raios são:
a) Radiações formadas por partículas alfa com grande poder de penetração.
b) Radiações formadas por elétrons dotados de grandes velocidades.
c) Ondas eletromagnéticas de frequências maiores que as das ondas ultravioletas.
d) Ondas eletromagnéticas de frequências menores do que as das ondas luminosas.
e) Ondas eletromagnéticas de frequências iguais as das ondas infravermelhas.
39) Um roteador wireless emite ondas eletromagnéticas com frequência de 5,0 GHz. Sabe-se que a velocidade de propagação desta onda, no ar, é igual à velocidade da luz no vácuo (c = 300 000 Km/s). Calcule o valor do comprimento de onda λ , em metros, para essa onda.
40) Uma onda propagando-se em um meio A, com comprimento de onda λ A = 2m, sofre refração e passa a se propagar em um meio B, com comprimento de onda λ B = 6m.
a) Das grandezas físicas frequência, período e velocidade de propagação, qual(is) permanece(m) inalterada(s)?
b) Se a frequência das ondas no meio A vale 30 Hz, qual será a velocidade de propagação dessa onda no meio B?
41) Uma emissora de rádio FM emite ondas de 100 MHz.Qual o comprimento das ondas? Lembre - se de que a velocidade de qualquer onda eletromagnética no vácuo ou no ar é de 300 000 Km/s.
42) (ENEM-2010) As ondas eletromagnéticas, como a luz visível e as ondas de rádio, viajam em linha reta em um meio homogêneo. Então, as ondas de rádio emitidas na região litorânea do Brasil não alcançariam a região amazônica do Brasil por causa da curvatura da Terra. Entretanto
sabemos que é possível transmitir ondas de rádio entre essas localidades devido à ionosfera. Com ajuda da ionosfera, a transmissão de ondas planas entre o litoral do Brasil e a região amazônica é possível por meio da
a) reflexão
b) refração.
c) difração.
d) polarização.
e) interferência.
43) Um certo alto-falante produz um som com freqüência de 2.0 Hz e uma intensidade de 0,960 mW/m2 à distância de 6,10 m. Supondo que não há reflexões e que o alto-falante emite igualmente em todas as direções.
(a) Qual é a intensidade a 30,0 m?
(b) Qual a amplitude de deslocamento a 6,10 m ?
(c) Qual a amplitude de pressão a 6,10 m?
44) Você tem quatro diapasões. O que tem a freqüência mais baixa oscila a 500 Hz. Oscilando dois diapasões, ao mesmo tempo, as seguintes freqüências serão ouvidas: 1, 2, 3, 5, 7 e 8 Hz. Quais as possíveis freqüências dos outros três diapasões?
Resoluções:
1) Veja na figura abaixo que um comprimento de onda λ vale --- 1,5λ/2=15 --- λ=15/1,5=10cm=0,1m --- equação

fundamental da ondulatória --- V=λf=0,1.740 --- V=74m/s.
2) Observe no gráfico fornecido que o período T (tempo que as ondas superficiais na superfície da água geradas pela aranha demoram para efetuar uma oscilação completa) vale T=4ms=4.10-3s --- frequência dessas ondas --- f=1/T ---
f=1/(4.10-3) --- f=0,25.103=250Hz --- equação fundamental da ondulatória --- v=λf=2.10-3.250 --- v=500.10-3m/s --- v=0,5m/s=50cm/s --- RESPOSTA - B.
3) a) f =lB --- 63.106=42.106.B --- B=1,5T Pelo gráfico, quando B=1,5T – x=1.0m
b) V=lf --- 3.108=l.63.106 --- l=0,0476.102 --- l=4,76m
4) Observando o gráfico você vê que, o período do batimento desse atleta é 0,5 s --- T=0,5s --- f=1/T=1/0,5 --- f=2Hz --- portanto, você tem 2 batimentos por segundo ou 2.60=120 batimentos por minuto --- Resposta- D
5) V = 1.188km/h = 330 m/s --- f = 2.640 Hz --- V=λf --- λ=V/f=330/2.640 --- λ=0,125m
6) Falsa – T=1/25 --- T=0,04s
Falsa – A=3m
Verdadeira – V=l.f --- V=0,2.25 --- V=5m/s
Verdadeira
Falsa -- l=20cm=0,2m
7) F=6/1,5=4Hz --- T=1/f=1/4=0,25s
8) a) f=40Hz --- T=1/f --- T=1/40 --- T=0,025=2,5.10-2s
b) V=l.f --- V=15.40 --- V=600cm/s=6m/s
9) RESPOSTA: C --- Como a freqüência diminui, o período que é seu inverso, aumenta.
10) RESPOSTA: C --- No vácuo todas essas radiações eletromagnéticas se propagam com velocidade constante de 3,0.108m/s e V= V=l.f
11) V=l.f --- V=2.6 --- V=12cm/s --- V=DS/Dt --- 12=60/Dt --- Dt=5s
12) RESPOSTA: C. l=150km -- V=750km/h --- V=l.f --- 750=150f --- f=5Hz --- T=1/f --- T=1/5h --- T=1/5.60 --- T=12min
13) Observe que, em cada 0,5s, cada crista ou cada vale ou cada ponto da onda percorre 1m
V=S/t --- V=1/05 --- V=2m/s
14) a) No gráfico da figura 1 --- T=5s --- f=1/T --- f=1/5 --- f=0,2Hz
b) No gráfico da figura 2 --- l=25m
c) V=l.f --- V=25.0,2 --- V=5m/s
d)
15) λ = 12 cm = 0,12 m --- c = 300.000 km/s = 3.108 m/s --- V=λf --- f=V/λ=3.108/0,12 --- f=2,5.109 Hz --- f=2,5MHz --- RESPOSTA- D
16) Observe na figura que --- equação da onda --- V=λf --- 10=λ.1 --- λ=10m --- comprimento da ponte ---
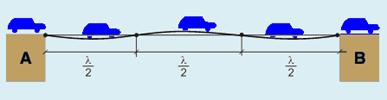
L=3λ/2 --- L=3.10/2 --- L=15m
17) 3 λ/2=0,51 --- 3λ=1,02 --- λ=0,34m --- equação fundamental da ondulatória --- V= λf --- 340=0,34.f --- f=1000Hz --- se a distância da pessoa ao obstáculo é d, o som vai e volta percorrendo 2d, com V=340m/s em ∆t=2,0s --- V=2d/∆t --- 340=2d/2,0 --- d=d=340m --- RESPOSTA- B.
18) a) De acordo com o gráfico a velocidade mínima ocorre quando V=1505m/s, na profundidade de 75m
b) 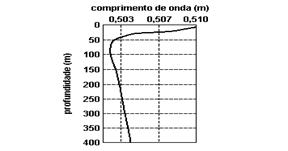

Refração
19)
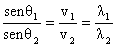
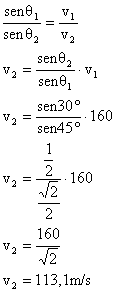
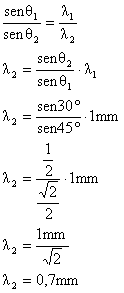



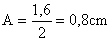
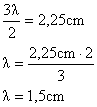
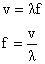

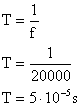 23) a) Da figura = 8,0 cm
23) a) Da figura = 8,0 cm

c)

29) I. Correta --- por exemplo, a luz é uma onda eletromagnética (não precisa de meio material para se propagar) transversal (direção de propagação é perpendicular à direção de oscilação).
Fontes: http://www.fisicaevestibular.com.br/exe_ond_2.htm
Solução:
Utilizando a Lei de Snell:
Utilizando a relação com velocidades de propagação, chegamos a equação:
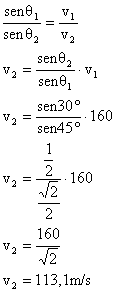
A velocidade da onda refratada será 113,1m/s.
Para calcular o comprimento de onda refratada, utilizamos a Lei de Snell, utilizando a relação com comprimentos de onda:
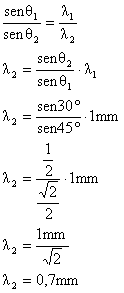
O comprimento da onda refratada será 0,7mm.
Repare que o resultado aparece em milímetros pois as unidades não foram convertidas para o SI no início da resolução.
20)
Solução:
A pessoa emite o som que bate no anteparo e volta.

V = ΔS/Δt
340 = 2D/0,1
2D = 34
D = 17 m
Letra C
21)
Solução:
Para entender a solução pense em uma onda da praia. Quando ela se aproxima de você, seu movimento é de subida. Após passar do ponto mais alto (velocidade nula no instante), começa a descida.

Assim acontece com os pontos da corda, observe:

Logo a velocidade do ponto A é vertical para baixo e a do ponto B é vertical para cima. O único ponto de velocidade nula momentânea seria o ponto médio do pulso.
Letra E
22) a) A Amplitude da onda é dada pela distância da origem até a crista da onda, ou seja:
b) O comprimento de onda é dado pela distância entre duas cristas ou entre 3 nodos, ou seja:
Como a figura mostra a medida de três "meios-comprimento de onda", podemos calculá-lo:
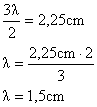
c) Sabendo a velocidade de propagação e o comprimento de onda, podemos calcular a frequência através da equação:
Substituindo os valores na equação:

d) Como o período é igual ao inverso da frequência:
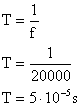
b) Na figura, temos dois pulsos completos:

c)

d) v = λ· f = 8 · 0,25 = 2,0 cm/s
e) Da figura a = 4,0 cm
e) Da figura a = 4,0 cm
24) Letra B.
25) Para retornar ao equilíbrio o ponto B deverá se deslocar de DSB = 60cm = 0,6m --- V = DSB/tB --- V = 0,6/tB
Para retornar ao equilíbrio o ponto A deverá se deslocar de DSA = 80cm = 0,8m --- V= DSA/tA --- V=0,8/tA
Como a velocidade é a mesma para os dois pontos --- 0,6/tB = 0,8/tA --- tA/tB = 4/3
26) Letra E.
27) Como o som vai e volta ele percorre ∆S=2h --- V=∆S/∆t ---1,6.103 = 2h/0,8 --- h=1,6.103.0,4 --- h=640m --- equação fundamental da ondulatória --- V=λ.f --- 1,6.103= λ.4.104 --- λ=1,6.103/4.104 --- λ=0,4.10-1=4.10-2m ---
RESPOSTA- A.
28) I. Correta --- essas três grandezas são escalares, pois ficam perfeitamente caracterizadas apenas pela intensidade acrescida de unidade, não precisando nem de direção e nem de sentido.
II. Correta --- O valor do campo gravitacional g não depende da massa m do corpo, mas apenas de sua posição r em relação ao centro planeta e da massa M do planeta --- você pode fazer analogia do campo gravitacional com os campos magnético e elétrico..
III. Falsa --- no estudo das ondas entra a grandeza velocidade que é uma grandeza vetorial, pois além de intensidade com unidade, possui também direção e sentido.
RESPOSTA- C
29) I. Correta --- por exemplo, a luz é uma onda eletromagnética (não precisa de meio material para se propagar) transversal (direção de propagação é perpendicular à direção de oscilação).
II. Correta --- variações no campo magnético produzem campos elétricos variáveis que, por sua vez, produzem campos magnéticos também variáveis e assim por diante, permitindo que energia e informações sejam transmitidas a grandes distâncias através das ondas eletromagnéticas que se propagam no vácuo com velocidade constante de 3,0.108m/s,, inclusive a luz
III. Correta --- Onda não transporta matéria, apenas energia.
30) Raio, relâmpago e trovão são fenômenos atmosféricos que ocorrem antes ou durante tempestades, causados por descargas elétricas entre nuvens ( relâmpago ) ou entre uma nuvem e o solo ( raio ), acompanhados de um estrondo ( trovão ) --- o raio ocorre quando uma nuvem, carregada de eletricidade estática, atinge um potencial eletrostático tão elevado que a camada de ar existente entre ela e o solo deixa de ser isolante, tornando-se condutor, permitindo a movimentação das cargas elétricas até o solo --- com o relâmpago ocorre a mesma coisa só que é entre as nuvens --- essas descargas elétricas produzem uma grande luminosidade devido ao aquecimento do ar, que pode ser vista bem distante --- o trovão é o som que acompanha a violenta expansão do ar quando é rapidamente aquecido --- devido à diferença de velocidades da luz e do som (luz, 3.108m/s e som, 340m/s), quando o raio ou relâmpago ocorre a grande distância do local de observação, o trovão é ouvido alguns segundos depois do clarão --- RESPOSTA- E.
31) (02+04+08=14)
32) Letra B.
33) Letra C.
34) Letra D.
35) Letra E.
36) a)
.gif)











36) a)
.gif)
b) Porque os metais refletem as ondas dentro dos fornos, o que diminui sua eficiência.
37) Infravermelho: significa ondas com frequência abaixo da luz vermelha. Essa luz vermelha é a luz visível de menor frequência.
Ultravioleta: tem esse nome porque possui ondas com frequência acima da luz violeta, que é a luz visível com maior frequência.
38) Os raios X são ondas eletromagnéticas com frequências maiores que as das ondas ultravioletas.
Alternativa C
39) A velocidade de propagação de uma onda é dada por: v = λ .f
Mas veja que,
v = c = 3 00 000 km/s = 3 00 000 000 m/s = 3.108 m/s.
f = 5 GHz = 5.10 9 Hz.
Assim,
λ = (v / f) = (3/5) . 10 -1 = 0,06 m.
40) a) Quando uma onda sofre refração, o que permanece invariável é a freqüência e o período.
b) Como a frequência é a mesma em qualquer um dos meios, ou seja, fA = fB, então podemos usar f = 30 Hz para calcular a velocidade no meio B. Para isto, basta usar a relação
vB = λB . fB = 6 x 30 = 180 m/s.
41) Para resolver questões de ondas, uma das coisas de que você precisa lembrar é a equação da velocidade de propagação de uma onda, que diz:
velocidade (v) = comprimento de onda (L) x frequência (f)
As ondas de rádio são ondas eletromagnéticas e a velocidade das ondas eletromagnéticas é de 300 000 Km/s ou 300 000 000 m/s. A frequência da onda foi dada: 100 MHz = 100 000 000 Hz. Substituindo essas informações na equação da velocidade, encontraremos o comprimento de onda em metros. Observe:
v = L.f
300 000 000 = L x 100 000 000
L = 300 000 000 / 100 000 000
L = 3 m
42) Letra A.
43) Considere o seguinte esquema:
(a) A intensidade sonora é definida como a potência transmitida pela onda por unidade de área da frente de onda, que, no presente caso, é esférica. Para a onda que chega ao ponto 1 temos:
Para a onda que chega ao ponto 2:
Logo:
I r
I r =

30 m rII r
(b) A intensidade I sonora depende do quadrado da amplitude de deslocamento sm de acordo com a seguinte relação:
Halliday, Resnick, Walker - Física 2 - 4 Ed. - LTC - 1996. Cap. 18 – Ondas I 9
Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES

()1 2mm 1mp vs v f sρω ρ πΔ= =

44) Para quem não conhece, um diapasão é um instrumento metálico (figura abaixo) capaz de vibrar numa freqüência bem definida, como, por exemplo, a da nota musical lá, que é de 440 Hz.

Sejam f1, f2, f3 e f4 as freqüências dos diapasões, sendo que f1 = 500 Hz é a menor das freqüências. A freqüência dos batimentos é dada por fbat = |fA − fB|, em que fA e fB são duas freqüências quaisquer.
Como todas as combinações de batimentos foram produzidas (12, 13, 14, 23, 24, 34) e três delas são com f1, que é a menor delas, deduz-se que os três batimentos de maior freqüência foram produzidos com f1. Logo:

http://soumaisenem.com.br/fisica/oscilacoes-ondas-optica-e-radiacao/ondas-fenomenos

uma onda estacionaria estabelece-se em uma corda de 50 cm fixa pelas extremidades. Incluindo-se as extremidades, observa-se, ao longo da corda, a formação de seis regiões nodais. Determine o comprimento de onda das ondas progressivas que originaram a onda estacionária.
ResponderExcluir9 questao está errada, é letra B, pois o periodo q diminui entao a frequencia aumenta
ResponderExcluirA questão 9 tem um pequeno erro na resposta, se a varinha tocava a água a cada 5s e agora passar a tocas a agua a cada 3s isso significa que a varinha tocara a água com maior frequencia, entao a frequência aumenta e o periodo que isso ocorre diminui.
ResponderExcluirAmei dos exercícios
ResponderExcluirAmei dos exercícios
ResponderExcluir
ResponderExcluir14. Um trem de ondas propaga-se ao longo de uma corda tensa. A figura a seguir representa a corda 8,0 segundos após o início do movimento. Determine, para essas ondas:
a) o comprimento de onda
b) a freqüência
c) o período
d) a velocidade de propagação
e) a amplitude.
Eu queria a reposta da questão 23 não aparece pra min
ResponderExcluir