Artigo sobre relações métricas no triângulo retângulo e aplicações do Teorema de Pitágoras geometria.
Observe a figura abaixo.

Temos que:
a: hipotenusa
a: hipotenusa
b e c: catetos
h: altura relativa a hipotenusa
m e n: projeções ortogonais dos catetos sobre a hipotenusa.
h: altura relativa a hipotenusa
m e n: projeções ortogonais dos catetos sobre a hipotenusa.
Relações métricas no triângulo retângulo
Observe os triângulos:
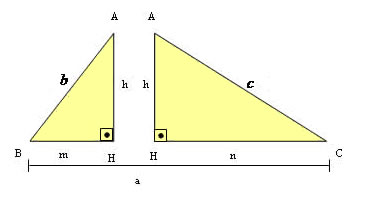
Da semelhança de triângulos obtemos as seguintes relações:
Observe os triângulos:

Da semelhança de triângulos obtemos as seguintes relações:
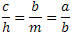
.jpg)
b2 = am e ah = bc
Temos, também, as seguintes relações:
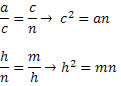
E a mais famosa das relações métricas no triângulo retângulo:
a2 = b2 + c2
Que é o teorema de Pitágoras.
Observe que temos cinco relações métricas no triângulo retângulo:
1. b2 = am
2. ah = bc
3. c2 = an
4. h2 = mn
5. a2 = b2 + c2
Neste triângulo ABC, vamos calcular a, h, m e n:

a² = b² + c² → a² = 6² + 8² → a² = 100 → a = 10
b.c = a.h → 8.6 = 10.h → h = 48/10 = 4,8
c² = a.m → 6² = 10.m → m = 36/10 = 3,6
b² = a.n → 8² = 10.n → n = 64/10 = 6,4
Determine os valores literais indicados na figura:

13² = 12² + x² 5.12 = 13.y
169 = 144 + x² y = 60/13
x² = 25
x = 5
169 = 144 + x² y = 60/13
x² = 25
x = 5
Aplicações do Teorema de Pitágoras
Altura de um triângulo equilátero
O triângulo PQR é equilátero, vamos calcular sua altura com base na medida l dos lados. Ao determinarmos a altura (h) do triângulo PQR, podemos observar um triângulo retângulo PHQ catetos: h e l/2 e hipotenusa h. Aplicando o teorema de Pitágoras temos:
.jpg)
.jpg)
O triângulo PQR é equilátero, vamos calcular sua altura com base na medida l dos lados. Ao determinarmos a altura (h) do triângulo PQR, podemos observar um triângulo retângulo PHQ catetos: h e l/2 e hipotenusa h. Aplicando o teorema de Pitágoras temos:
.jpg)
.jpg)
Um terreno retangular possui as seguintes medidas: 20 metros de comprimento e 30 metros de largura. Determine a medida da diagonal desse terreno.
.jpg)
A diagonal divide o retângulo em dois triângulos retângulos, consistindo na hipotenusa deles. Portanto, utilizaremos o Teorema de Pitágoras para determinar a medida da diagonal. Veja:
d² = 30² + 20²
d² = 900 + 400
d² = 1300
√d² = √1300
d = 36 metros (aproximadamente)
d² = 30² + 20²
d² = 900 + 400
d² = 1300
√d² = √1300
d = 36 metros (aproximadamente)
Nenhum comentário:
Postar um comentário