Toda função estabelecida pela lei de formação f(x) = ax² + bx + c, com a, b e c números reais e a ≠ 0, é denominada função do 2º grau. Generalizando temos:
A representação geométrica de uma função do 2º grau é dada por uma parábola, que de acordo com o sinal do coeficiente a pode ter concavidade voltada para cima ou para baixo.
.jpg)
As raízes de uma função do 2º grau são os pontos onde a parábola intercepta o eixo x. Dada a função f(x) = ax² + bx + c, se f(x) = 0, obtemos uma equação do 2º grau, ax² + bx + c = 0, dependendo do valor do discriminante ? (delta), podemos ter as seguintes situações gráficas:
? > 0, a equação possui duas raízes reais e diferentes. A parábola intercepta o eixo x em dois pontos distintos.
.jpg)
? = 0, a equação possui apenas uma raiz real. A parábola intercepta o eixo x em um único ponto.
.jpg)
? > 0, a equação possui duas raízes reais e diferentes. A parábola intercepta o eixo x em dois pontos distintos.
.jpg)
? = 0, a equação possui apenas uma raiz real. A parábola intercepta o eixo x em um único ponto.
.jpg)
? < 0, a equação não possui raízes reais. A parábola não intercepta o eixo x.
.jpg)
.jpg)
Uma função do 2º grau é definida pela seguinte lei de formação f(x) = ax² + bx + c ou y = ax² + bx + c, onde a, b e c são números reais e a ≠ 0. Sua representação no plano cartesiano é uma parábola que, de acordo com o valor do coeficiente a, possui concavidade voltada para cima ou para baixo. A função do 2º grau assume três possibilidades de resultados ou raízes, que são determinadas quando fazemos f(x) ou y igual a zero, transformando a função numa equação do 2º grau, que pode vir a ser resolvida por Bháskara.
Gráfico da função
Coeficiente a > 0, parábola com a concavidade voltada para cima
Coeficiente a < 0, parábola com a concavidade voltada para baixo
? > 0 – A equação do 2º grau possui duas soluções distintas, isto é, a função do 2º grau terá duas raízes reais e distintas. A parábola intersecta o eixo das abscissas (x) em dois pontos.
Gráfico da função
Coeficiente a > 0, parábola com a concavidade voltada para cima
Coeficiente a < 0, parábola com a concavidade voltada para baixo
? > 0 – A equação do 2º grau possui duas soluções distintas, isto é, a função do 2º grau terá duas raízes reais e distintas. A parábola intersecta o eixo das abscissas (x) em dois pontos.
.jpg)
? = 0 – A equação do 2º grau possui uma única solução, isto é, a função do 2º grau terá apenas uma raiz real. A parábola irá intersectar o eixo das abscissas (x) em apenas um ponto.
.jpg)
? < 0 – A equação do 2º grau não possui soluções reais, portanto, a função do 2º grau não intersectará o eixo das abscissas (x).
.jpg)
Pontos notáveis do gráfico de uma função do 2º grau
O vértice da parábola constitui um ponto importante do gráfico, pois indica o ponto de valor máximo e o ponto de valor mínimo. De acordo com o valor do coeficiente a, os pontos serão definidos, observe:
Quando o valor do coeficiente a for menor que zero, a parábola possuirá valor máximo.
.jpg)
Quando o valor do coeficiente a for maior que zero, a parábola possuirá valor mínimo.
.jpg)
Outra relação importante na função do 2º grau é o ponto onde a parábola corta o eixo y. Verifica-se que o valor do coeficiente c na lei de formação da função corresponde ao valor do eixo y onde a parábola o intersecta.
.jpg)
Raízes da Função de 2º Grau
Determinar a raiz de uma função é calcular os valores de x que satisfazem a equação do 2º grau ax² + bx + c = 0, que podem ser encontradas através do Teorema de Bháskara:
.jpg)
Número de raízes reais da função do 2º grau
Dada a função f(x) = ax² + bx + c, existirão três casos a serem considerados para a obtenção do número de raízes. Isso dependerá do valor do discriminante Δ.
1º caso → Δ > 0: A função possui duas raízes reais e distintas, isto é, diferentes.
2º caso → Δ = 0: A função possui raízes reais e iguais. Nesse caso, dizemos que a função possui uma única raiz.
3º caso → Δ < 0: A função não possui raízes reais.
Soma e produto das raízes
Seja a equação, ax² + bx + c = 0, temos que:
Se Δ ≥ 0, a soma das raízes dessa equação é dada por.jpg) e o produto das raízes por
e o produto das raízes por .jpg) . De fato, x’ e x’’ são as raízes da equação, por isso temos:
. De fato, x’ e x’’ são as raízes da equação, por isso temos:
.jpg)
Soma das raízes
.jpg)
Produto das raízes
.jpg)
Efetuando a multiplicação, temos:
.jpg)
Substituindo Δ por b² – 4ac, temos:
.jpg)
Após a simplificação, temos:
.jpg)
.jpg)
Número de raízes reais da função do 2º grau
Dada a função f(x) = ax² + bx + c, existirão três casos a serem considerados para a obtenção do número de raízes. Isso dependerá do valor do discriminante Δ.
1º caso → Δ > 0: A função possui duas raízes reais e distintas, isto é, diferentes.
2º caso → Δ = 0: A função possui raízes reais e iguais. Nesse caso, dizemos que a função possui uma única raiz.
3º caso → Δ < 0: A função não possui raízes reais.
Soma e produto das raízes
Seja a equação, ax² + bx + c = 0, temos que:
Se Δ ≥ 0, a soma das raízes dessa equação é dada por
.jpg)
Soma das raízes
.jpg)
Produto das raízes
.jpg)
Efetuando a multiplicação, temos:
.jpg)
Substituindo Δ por b² – 4ac, temos:
.jpg)
Após a simplificação, temos:
.jpg)
Exercícios Propostos
1) A representação cartesiana da função  é a parábola abaixo. Tendo em vista esse gráfico, podemos afirmar que:
é a parábola abaixo. Tendo em vista esse gráfico, podemos afirmar que:
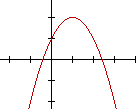
| (A) a<0, b<0 e c>0 (B) a>0, b>0 e c<0 (C) a>0, b>0 e c>0 (D) a<0, b>0 e c<0 (E) a<0, b>0 e c>0
2) Qual a função que representa o gráfico seguinte?
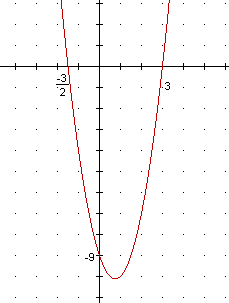
(A)
(B) (C) (D) (E) 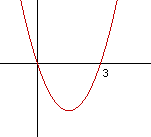
(A)
(B)
(C)
(D)
(E)
(A) (B) (C) (D) (E) 5) (UFRGS) O movimento de um projétil, lançado para cima verticalmente, é descrito pela equação (A) 6,25 m, 5s (B) 250 m, 0 s (C) 250 m, 5s (D) 250 m, 200 s (E) 10.000 m , 5s 6) (UFRGS) Considere a função (A) não intercepta o eixo das abscissas (B) intercepta o eixo horizontal em dois pontos, de abscissas negativa e positiva respectivamente (C) intercepta o eixo das abscissas em um único ponto (D) intercepta o eixo das abscissas em dois pontos, ambos positivos. (E) intercepta o eixo das ordenadas em dois pontos. 7) A razão entre a soma e o produto das raízes da equação (A) (B) (C) (D) (E) 8) A solução de (A) (0, 1) (B) (-∞, 0)U(1, +∞) (C) (-1, 1) (D) (-∞, -1)U(1,+∞) (E) R 9) (UFRGS) Para que a prábola da equação (A) (B) (C) (D) (E) 10) O vértice da parábola que corresponde à função (A) (-2, -2) (B) (-2, 0) (C) (-2, 2) (D) (2, -2) (E) (2, 2) GABARITO: 1) E 2) C 3) C 4) D 5) C 6) B 7) A 8) A 9) B 10) E |
Na número 5 após resposta não seria 25m em 2,5s, pois o yv= 200:80 = 2.5
ResponderExcluirPerdão concordo com unknown.
ResponderExcluir