Em termos simples o logaritmo é o expoente que uma dada base deve ter para produzir certa potência. Usualmente é escrito como logb x = y. Por exemplo:
 portanto
portanto  No exemplo o logaritmo de 81 na base 3 é 4, pois 4 é o expoente que a base 3 deve usar para resultar 81.
No exemplo o logaritmo de 81 na base 3 é 4, pois 4 é o expoente que a base 3 deve usar para resultar 81.Exemplo 2:
log10100 = b ⇔ 10b = 100
Como 100 = 102, repare: 100 = 10 ·10 = 102
Então 10b = 100 = 10 2 ⇔ y = 2. Portanto, log10 100= 2 pois 102 = 100.
Propriedades dos logaritmos
P1) O logaritmo da unidade em qualquer base é nulo, ou seja:loga1 = 0 porque a0 = 1.
P2) O logaritmo da base é sempre igual a 1, ou seja: logbb = 1 , porque b1 = b.
P3) alogab = b ou seja: a elevado ao logaritmo de b na base a é igual a b.
P4) logaak = k, porque ak = ak.
P5) Se logab = logac então podemos concluir que b = c. Esta propriedade é muito utilizada na solução de exercícios envolvendo equações onde aparecem logaritmos (equações logarítmicas).
Logaritmo do Produto
É a propriedade que o logaritmo do produto de números reais positivos seja a soma dos logaritmos dos fatores, ou seja: loga(b.c) = logab + logac onde: b > 0, c > 0, a > 0 e a ≠ 1.
É possível transformar o logaritmo do produto numa soma de logaritmos.
Ex: log20 =log(2.10) = log2 + log10 = 0,3010 + 1 = 1,3010. Observe que como a base não foi especificada, sabemos que ela é igual a 10.
Ex2: Vamos calcular log28 e log24.
Log28 = 3 pois 23 = 8 e log24 = 2 pois 22 = 4.
Para calcularmos log2 (8.4), basta somarmos os logaritmos de 8 e de 4 que acabamos de calcular:
log2 (8.4) = Log28 + log24log2 (8.4) = 3 + 2
log2 (8.4) = 5
O logaritmo de uma fração ordinária é igual a diferença entre os logaritmos do numerador da fração e do denominador, ou seja: loga(b/c) = logab – logac.
Loga(b/c) = log a b - log a b
Ex: Vamos calcular log28 e log24.
Ex: Vamos calcular log28 e log24.
Log28 = 3 pois 23 = 8 e log24 = 2 pois 22 = 4.
Para calcularmos log2 (8/4), basta subtrairmos os logaritmos de 8 e de 4 que acabamos de calcular:
Ex2: Primeiramente, note que 0,25 é 1/4 (um quarto).log2 (8/4) = Log28 - log24log2 (8/4) = 3 - 2
log2 (8/4) = 1
Pela propriedade de logaritmo temos que
log2 [0,25] = log2 [1/4] = log2 [ 1 : 4] = log2 [ 1 ] – log2 [ 4 ] = 0 – 2 = –2.
log2 4 = y ⇔ 2y = 4 ⇔ y = 2. Portanto, log2 4= 2 pois 22 = 4.
log2 1 = z ⇔ 2z = 1 ⇔ z = 0. Portanto, log2 1= 0 pois 20 = 1.
Portanto, log2 0,25 = –2
Logaritmo da Potência
Temos a seguinte fórmula, facilmente demonstrável: logabk = k.logab.
Ex: log5256 = 6.log525 = 6.2 = 12.Ex2: Calcular log 0,001 .
log10 [0,001] = log10 [ 10–3] = (–3) ·log10 [ 10 ] = (–3) ·1 = –3
Repare que log10 [ 10 ] = y ⇔ 10y = 10 ⇔ y = 1.
Portanto, log10 0,001= –3.
Mudança de base
Às vezes, para solucionar problemas, necessitamos mudar a base de um sistema de logaritmos, ou seja, conhecemos o logaritmo de A na base b e desejamos obter o logaritmo de A numa base c.
| a base nova "c", pode ser qualquer número que satisfaça a condição de existência da base, ou seja, c > 0 e c ≠ 1. |
Esta mudança de base, muito importante na solução de exercícios, poderá ser feita de acordo com a fórmula a seguir, cuja demonstração não apresenta dificuldades, aplicando-se os conhecimentos aqui expostos.
Loga b = logcb/logca
Ex:
(UFRGS) Sabendo que  e
e 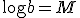 , então o logaritmo de a na base b é
, então o logaritmo de a na base b é
(A) 
(B)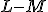
(C)
(B)
(C)
(D) 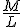
(E) 
| É dado o valor do logaritmo de a na base 10 e é pedido o logaritmo de a na base b. Para adequar o pedido ao informado, vamos transformar o Este valor encontrado possui termos que foram dados no enunciado, portanto, podemos substituir: |
Questões de vestibular sobre Logaritmos
01. Calcule o Log24 6 sabendo que o Log27 6 = x que o Log27 4 = y.
Solução:
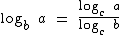
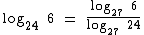
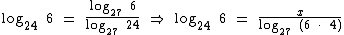
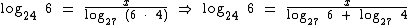
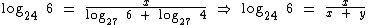
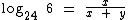 .
.


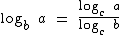
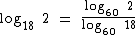
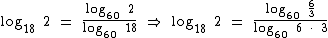
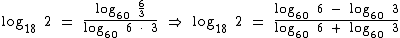
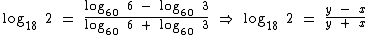
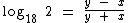 .
.
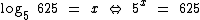
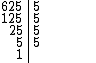
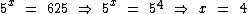
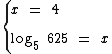
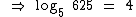
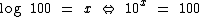
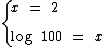
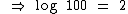
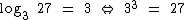
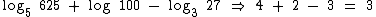
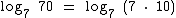
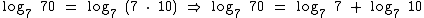
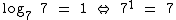
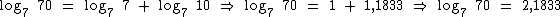
A primeira vista parece uma grande confusão, mas nota-se que existe uma base 2 e um log de 2. Logo, deve-se mudar para a base 2.
Nota: No caso de dúvida entre várias bases que sejam múltiplos (ex: 3, 9, 81, ...), em princípio, escolhe-se a menor.
Resolvendo com a mudança de base para 2:
Note que como os dois logaritmos possuem base 2, pode se usar a fórmula de mudança de base ao inverso, logo:
09. Resolva:
Solução:
À primeira vista, um problema complexo, com muitas bases diferentes, mas, ao ser analisado parte por parte:
 pois, somente um número elevado a zero resulta em 1;
pois, somente um número elevado a zero resulta em 1; também um log que a base ajuda bastante;
também um log que a base ajuda bastante; é um pouco mais interessante, mas, nada de amedrontar, pois as bases se "aparentam" entre si, logo:
é um pouco mais interessante, mas, nada de amedrontar, pois as bases se "aparentam" entre si, logo:
Utilize a propriedade do logaritmo de potência:
Finalmente:
Fórmula de mudança de base:
Mudando para a base 2:
Retornando à equação original com os resultados:
12. (PUCRS) Se 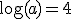 e
e  , então
, então  é igual a
é igual a


15. (UFRN) O valor da expressão log2 64 – log3 27 é igual a:

16. (ITA-SP) log216 – log432 é igual a:



 ., é:
., é:
 18. (Vunesp) Sejam x e y números reais, com x > y. Se log3(x – y) = m e (x + y) = 9, determine:
18. (Vunesp) Sejam x e y números reais, com x > y. Se log3(x – y) = m e (x + y) = 9, determine:

 a soma das raízes será 101. S = {101}
a soma das raízes será 101. S = {101}
Solução:
Para a resolução deste problema vamos partir do princípio que:
Esta é a propriedade que nos permite realizar a mudança de base de um logaritmo.
Recorrendo a ela temos:
Como o Log27 6 = x, podemos realizar tal substituição na equação. Além disto iremos aproveitar para escrever o logaritmando 24, no denominador da fração, como o produto de 6 por 4:
Agora vamos recorrer à propriedade do logaritmo de um produto:
Já que o Log27 6 = x e o Log27 4 = y, vamos realizar estas substituições na equação:
Portanto:


05. Se o Log60 3 = x que o Log60 6 = y, qual é o Log18 2?
Solução:
O objetivo desta questão é escrevermos o Log18 2 em função de x e y.
Para alcançarmos tal objetivo faremos algumas operações para que partindo do Log18 2, passemos pelos Log60 3e de Log60 6.
Para começar vamos passar o Log18 2 para a base 60.
Para isto vamos recorrer à propriedade da mudança de base de um logaritmo:
Então para a = 2, b = 18 e c = 60, temos:
O logaritmando 2, no numerador da fração pode ser escrito como a razão de 6 para 3, assim como o logaritmando 18, no denominador da fração pode ser escrito como produto de 6 por 3. O motivo disto é nos direcionarmos aos logaritmos no enunciado:
No numerador vamos aplicar a propriedade do logaritmo de um quociente e no denominador a propriedade do logaritmo de um produto, quando aí sim, iremos obter os logaritmos no enunciado:
Pronto, agora chegamos a um ponto no qual só precisamos trocar o Log60 3 e o Log60 6 por x e y, respectivamente:
06. Calcule: Log5 625 + Log 100 - Log3 27?
Solução:
Vamos calcular cada um dos logaritmos separadamente.
O Log5 625 é o expoente da potência de base 5 que resulta em 625:
Podemos resolver a equação exponencial decompondo 625 em fatores primos:
Ou seja, 625 = 54, o que nos leva ao valor de x:
Pudemos calcular o valor de x desta forma, pois a a base 5 é positiva e diferente de 1. Se você não se lembra disto, convém consultar o tema equação exponencial para recordar esta matéria.
Então 4 é o Log5 625:
O Log 100 é o expoente da potência de base 10 que resulta em 100:
O valor de x agora é óbvio.
Como sabemos, uma potência de dez com expoente natural resulta em um número começando pelo algarismo 1 seguido de tantos zeros quanto indicado por este expoente.
Sabendo-se disto, se o número 100 possui 2 zeros após o 1, é porque o expoente da potência de base dez é igual a dois (102 = 100), isto é, x = 2.
Então 2 é o Log 100:
Por último, o Log3 27 é igual a 3, pois este é o expoente ao qual devemos elevar a base também 3 para obtermos 27:
Se você tem dúvidas quanto a isto, também pode decompor o número 27 em fatores primos como fizemos com oLog5 625.
Realizando as substituições na expressão original temos:
Log5 625 + Log 100 - Log3 27 = 3.
07. Considerando-se Log7 10 = 1,1833. Qual é o Log7 70?
Solução:
Para a solução deste problema vamos recorrer à propriedade do logaritmo de um produto.
Utilizaremos esta propriedade, pois através dela podemos montar uma outra expressão com dois logaritmos conhecidos. Um é o Log7 10, obtido do enunciado e o outro é o Log7 7 que como sabemos é igual a 1.
É sabido que 70 é o produto de 7 por 10. Então temos que:
Através da propriedade do logaritmo de um produto podemos assim expressar o Log7 70:
O Log7 7 = 1 pois:
Conforme o enunciado, o Log7 10 = 1,1833, então substituindo tais valores na expressão, temos:
Log7 70 = 2,1833.
08. Simplifique:
log25 . log72
Solução:A primeira vista parece uma grande confusão, mas nota-se que existe uma base 2 e um log de 2. Logo, deve-se mudar para a base 2.
Nota: No caso de dúvida entre várias bases que sejam múltiplos (ex: 3, 9, 81, ...), em princípio, escolhe-se a menor.
Resolvendo com a mudança de base para 2:
 |
Note que como os dois logaritmos possuem base 2, pode se usar a fórmula de mudança de base ao inverso, logo:
 |
 |
À primeira vista, um problema complexo, com muitas bases diferentes, mas, ao ser analisado parte por parte:
 pois, somente um número elevado a zero resulta em 1;
pois, somente um número elevado a zero resulta em 1; também um log que a base ajuda bastante;
também um log que a base ajuda bastante; é um pouco mais interessante, mas, nada de amedrontar, pois as bases se "aparentam" entre si, logo:
é um pouco mais interessante, mas, nada de amedrontar, pois as bases se "aparentam" entre si, logo:Utilize a propriedade do logaritmo de potência:
 |
 |
Finalmente:
 |
Fórmula de mudança de base:
 |
Mudando para a base 2:
 |
Retornando à equação original com os resultados:
 10. (UFRGS) Se
(A)
(B)
(C)
(D)
(E)
Solução:
Este tipo de questão começamos fatorando o termo que estiver no logaritmando:
Agora podemos aplicar as propriedades de radiciação :
Então as propriedades operatórias dos logaritmos:
Agora é só substituir os valores dados no enunciado:
Resposta certa, letra "D".
11. Dado
(A)
(B)
(C)
(D)
(E)
Solução:
Foi dado apenas uma informação, o valor de
Portanto, devemos moldar os valores no logaritmo que está sendo pedido em função do número 5. Veja só, vamos fatorar o 200:
Aplicar as propriedades dos logaritmos:
Só que o problema agora é descobrir o valor de
Sabemos que log 10 = 1 e log 5 = P, portanto, log 2 = 1 - P.
Agora que sabemos o valor de log 2 = 1 - P e log 5 = P podemos descobrir o valor de log 200.
Resposta correta, "D".
|
(A) 
(B) 
(C) 
(D)
(E)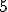
(D)
(E)
| Agora a questão é ao contrário. Começamos aplicando as propriedades operatórias no logaritmo pedido: Agora sim substituimos os valores dados no enunciado na expressão acima: Resposta correta, letra "B" |
13. Determine o número real x que satisfaz a equação log2(12 – 2x) = 2x.
Solução:
Condição 12 – 2x > 0
log2(12 – 2x) = 2x
12 – 2x = 22x
22x + 2x – 12 = 0
2x = y
y² + y – 12 = 0 (equação do 2º grau)
log2(12 – 2x) = 2x
12 – 2x = 22x
22x + 2x – 12 = 0
2x = y
y² + y – 12 = 0 (equação do 2º grau)
? = b² – 4ac
? = 1² – 4 * 1 * (-12)
? = 1 + 48
? = 49
? = 1² – 4 * 1 * (-12)
? = 1 + 48
? = 49


14. Considerando-se que x = 21000 e sabendo que log2 é aproximadamente igual a 0,30103, determine o número de algarismos de x.
Solução:
Logx = Log21000 → 1000 * Log2 → 1000 * 0,30101 → 301
a) 3 b) 13 c) 17 d) 31 e) 37
Solução:

Resposta: A
a)  d) 4
d) 4
b)  e) 1
e) 1
c) 
Solução:
Resposta: B
17. (Uneb-BA) O número real x, tal que logx
a)  d)
d) 
b)  e)
e) 
c) 
Solução:

a) o valor de log3(x + y);
b) log3(x2 – y2), em função de m.
Solução:
a) log3(x + y) = log39 = 2.
b) log3(x2 – y2) = log3 [(x + y) · (x – y)] =
log3 (x + y) + log3 (x – y) = m + 2.
19. Se log 2 = x e log 3 = y, então log 72 é igual a:
a) 2x + 3y
b) 3x + 2y
c) 3x – 2y
d) 2x – 3y
e) x + y
Solução:
log72 = log(23 · 32) = log23 + log32 =
= 3 · log2 + 2 · log3 = 3x + 2y
Resposta: B
20. (UFF-RJ) Sendo log a = 11, log b = 0,5, log c = 6 e log  = x, o valor de x é:
= x, o valor de x é:

21. (PUC-SP) Um estudante quer resolver a equação 2x = 5, utilizando uma calculadora que possui a tecla log x. Para obter um valor aproximado de x, o estudante deverá usar a calculadora para obter os seguintes números:
a) 5
b) 10
c) 15
d) 20
e) 25
Solução:

Resposta: B
a) log 2, log 5 e log 5 – log 2
b) log 2, log 5 e log 5 : log 2
c) log 2, log 5 e log 25
d) 5/2 e log 5/2
e)  e log
e log 
Solução:
Aplicando logaritmo com base 10 nos dois membros temos:
log 2x = log 5
x · log 2 = log 5 Þ x = 
Resposta: B
22. (FGV-SP) A equação logarítmica log2 (x + 1) + log2 (x – 1) = 3 admite:
a) uma única raiz irracional.
b) duas raízes opostas.
c) duas raízes cujo produto é – 4.
d) uma única raiz e negativa.
e) uma única raiz e maior do que 2.
Resolução
Condição de existência:
x + 1 > 0 Þ x > – 1 ; x – 1 > 0 Þ x > 1.
Assim x > 1
log2 (x + 1) · (x – 1) = 3
log2 (x2 – 1) = 3 Þ x2 – 1 = 23 Þ x2 – 1 = 8
x = 3
Resposta: E
23. (Cesgranrio-RJ) Se log x representa o logaritmo decimal do número positivo x, a soma das raízes de
log2 x – log x2 = 0 é:
log2 x – log x2 = 0 é:
a) – 1
b) 1
c) 20
d) 100
e) 101
Solução:
Condição de existência: x > 0
log2 x – log x2 = 0  log2 x – 2 log x = 0
log2 x – 2 log x = 0
Fazendo log x = y, obteremos:
y2 – 2y = 0  y(y – 2) = 0
y(y – 2) = 0  y = 0 ou y = 2
y = 0 ou y = 2
log x = 0  x = 1
x = 1
log x = 2  x = 100
x = 100
Resposta: E









 n 6 =
n 6 =  n (1,02)x
n (1,02)x
 n (2 · 3) = x ·
n (2 · 3) = x ·  n(1,02)
n(1,02)
 n 2 +
n 2 +  n 3 = x · 0,02
n 3 = x · 0,02

 · e – t /250
· e – t /250 
 = e – t /250
= e – t /250 
 n 2–2 = ln e–t/250
n 2–2 = ln e–t/250

 I = 10–12 W/m2 (Verdadeira)
I = 10–12 W/m2 (Verdadeira)
35. Resolva a equação
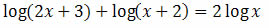
Solução: usando as propriedades do logaritmo, podemos reescrever a equação acima da seguinte forma:
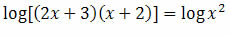
Note que para isso utilizamos as seguintes propriedades:
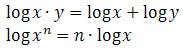
Vamos retornar à equação:
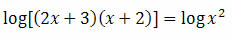
Como ficamos com uma igualdade entre dois logaritmos, segue que:
(2x +3)(x + 2) = x2
ou
2x2 + 4x + 3x + 6 = x2
2x2 – x2 + 7x + 6 = 0
x2 + 7x + 6 = 0
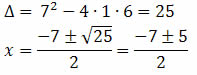
x = -1 ou x = - 6
Lembre-se que para o logaritmo existir o logaritmando e a base devem ser positivos.
Com os valores encontrados para x, o logaritmando ficará negativo. Sendo assim, a equação não tem solução ou S = ø.

Solução:CE: Como a incógnita x não está presente no logaritmando nem na base do logaritmo, não há restrições para o valor de x. Portanto, x E R.
Eliminado o parênteses temos:
Usando as propriedades dos logaritmos:

Como não há restrições para o valor de x temos: S = {-2, 0}.
Solução:Condição de existência: x > 0 e y > 0
Na primeira equação temos: log x + log y = 7 => log y = 7 – log x
Substituindo log y na segunda equação temos:
3.log x–2.(7–log x) =1 => 3.log x – 14 + 2.log x = 1
5.log x = 15 =>log x = 3 => x=103³
Como x = 10³ e log y = 7 – log x, então:
7 – log x = 7 – log 103 => log y = 7 – 3 => log y = 4 => y = 104.
Como satisfazem à CE, temos:

Solução:Usando a propriedade do logaritmo da potência ao inverso temos:

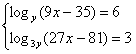
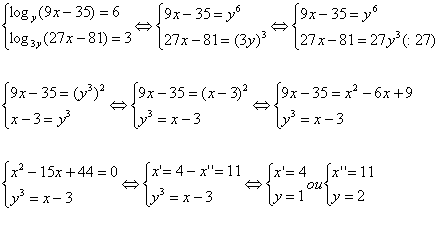
A condição é para y > 1, então, o conjunto solução é dado por x = 11 e y = 23.
24. (FGV-SP) O produto (log92) · (log25) · (log53) é igual a:
a) 0 d) 30
b)  e)
e) 
c) 10
Solução:
x = 


Resposta: B
25. A expressão  é equivalente a:
é equivalente a:
a) log250 d) log2 2
b) log2 10 e) log2
e) log2
c) log2 5 
Solução
log2 3 · log3 5 · log5 10 = log2 10 e
Portanto
log2 10 + log2 = log2 10
= log2 10
Resposta: B
26. (FCMSC-SP) São dados:
log15 3 = a e log15 2 = b. O valor de log10 2 é:
a) 
b) 
c) 
d) 
e) 
Solução:

Resposta: B
27. (Vunesp) Os biólogos dizem que há uma alometria entre duas variáveis, x e y, quando é possível determinar duas constantes, c e n, de maneira que y = c · xn. Nos casos de alometria, pode ser conveniente determinar c e n por meio de dados expe-rimentais. Consideremos uma experiência hipotética na qual se obtiveram os dados da tabela a seguir.
Supondo que haja uma relação de alometria entre x e y e considerando log 2 = 0,301, determine o valor de n.

Solução:
y = c · xn
16 = c · 2n
log 16 = log c · 2n
log 24 = log c + log 2n
4 · log 2 = log c + n · log 2 (I)
40 = c · (20)n log 40 = log [c · (20)n]
log 4 · 10 = log c + log (20)n
log 4 + log 10 = log c + n · log 20
log 22 + 1 = log c + n · log (2 · 10)
2 · log 2 + 1 = log c + n · (log 2 + log 10)
2 · log 2 + 1 = log c + n · log 2 + n (II)
Fazendo (I) – (II), temos:
2 · log 2 – 1 = –n
n = 1 – 2 · log 2 = 0,398
Resposta: n = 0,398
28. (UFC-CE) Suponha que o nível sonoro b e a intensidade I de um som estejam relacionados pela equação logarítmica b = 120 + 10 log10 I, em que b é medido em decibéis e I, em watts por metro quadrado. Sejam I1 a intensidade correspondente ao nível sonoro de 80 decibéis de um cruzamento de duas avenidas movimentadas e I2 a intensidade correspondente ao nível sonoro de 60 decibéis do interior de um automóvel com ar-condicionado. A razão I1/I2 é igual a:
a) 1/10 d) 100
b) 1 e) 1 000
c) 10
Solução:
80 = 120 + 10 · log10 I1  – 40 = 10 · log10 I1
– 40 = 10 · log10 I1
log10 I1 = – 4  I1 = 10–4
I1 = 10–4
60 = 120 + 10 · log10 I2  – 60 = 10 · log10 I2
– 60 = 10 · log10 I2
log10 I2 = – 6  I2 = 10 –6
I2 = 10 –6
Resposta: D
29. O anúncio de certo produto aparece diaria-mente num certo horário na televisão. Após t dias do início da exposição, o número de pessoas (y) que ficam conhecendo o produto é dado por
y = 3 – 3 · (0,95)t, onde y é dado em milhões de pessoas.
Para que valores de t teremos pelo menos 1,2 milhão de pessoas conhecendo o produto?
Solução:
y  1,2
1,2  3 – 3 · (0,95)t
3 – 3 · (0,95)t  1,2
1,2  –3 · (0,95)t
–3 · (0,95)t  –1,8
–1,8
(0,95)t  0,6
0,6
log0,95 (0,95)t  log0,95 0,6 (base entre 0 e 1)
log0,95 0,6 (base entre 0 e 1)
t  log0,95 0,6
log0,95 0,6
Resposta: t  log0,95 0,6
log0,95 0,6
30. (UnB-DF) Estima-se que 1 350 m2 de terra sejam necessários para fornecer alimento para uma pessoa. Admite-se, também, que há 30 × 1 350 bilhões de m2 de terra arável no mundo e que, portanto, uma população máxima de 30 bilhões de pessoas pode ser sustentada, se não forem exploradas outras fontes de alimento. A população mundial, no início de 1987, foi estimada em 5 bilhões de habitantes. Considerando que a população continua a crescer, a uma taxa de 2% ao ano, e usando as aproximações  n 1,02 = 0,02;
n 1,02 = 0,02;  n 2 = 0,70 e
n 2 = 0,70 e  n 3 = 1,10, determine em quantos anos, a partir de 1987, a Terra teria a máxima população que poderia ser sustentada.
n 3 = 1,10, determine em quantos anos, a partir de 1987, a Terra teria a máxima população que poderia ser sustentada.
Solução:
Se a taxa de crescimento é de 2% ao ano, depois de um ano a população, em bilhões de habitantes, será 5 · 1,02. Depois de x anos será 5 · (1,02)x.
Logo, para as condições do problema:
30 = 5 · (1,02)x  6 = (1,02)x
6 = (1,02)x
0,70 + 1,10 = x · 0,02  1,80 = x · 0,02
1,80 = x · 0,02
x = 90
Resposta: 90 anos
31. (UFMG) O pH de uma solução aquosa é definido pela expressão pH = –log [H+], em que [H+] indica a concentração, em mol/L, de íons de hidrogênio na solução e log, o logaritmo na base 10.
Ao analisar uma determinada solução, um pesquisador verificou que, nela, a concentração de íons de hidrogênio era [H+] = 5,4 · 10–8 mol/L. Para calcular o pH dessa solução, ele usou os valores aproximados de 0,30, para log 2, e de 0,48, para log 3.
Então, o valor que o pesquisador obteve para o pH dessa solução foi:
a) 7,26 c) 7,58
b) 7,32 d) 7,74
Solução:
pH = –log [H+] = –log 5,4 · 10–8
pH = –(log 5,4 + log 10–8)
pH = –(log 54/10 + (–8))
pH = –(log 54 – log 10 – 8)
pH = –(log (33 · 2) – 1 – 8) = –(log 33 + log 2 – 9)
pH = –(3 · 0,48 + 0,30 – 9)
pH = 7,26
Resposta: A
32. (PUC-SP) A energia nuclear, derivada de isótopos radiativos, pode ser usada em veículos espaciais para fornecer potência. Fontes de energia nuclear perdem potência gradualmente, no decorrer do tempo. Isso pode ser descrito pela função exponencial
na qual P é a potência instantânea, em watts, de radioisótopos de um veículo espacial; P0 é a potência inicial do veículo; t é o intervalo de tempo, em dias, a partir de t0 = 0; e é a base do sistema de logaritmos neperianos. Nessas condições, quantos dias são necessários, aproximadamente, para que a potência de um veículo espacial se reduza à quarta parte da potência inicial? (Dado: ln 2 = 0,693)
a) 336 d) 342
b) 338 e) 346
c) 340
Solução:
Para P 
–2 ·  n 2 =
n 2 = 
 2 · 0,693 · 250 = t
2 · 0,693 · 250 = t
t = 346,1  346
346
Resposta: E
33. (UFF-RJ) No dia 6 de junho de 2 000, um terremoto atingiu a cidade de Ancara, na Turquia, com registro de 5,9 graus na escala Richter e outro terremoto atingiu o oeste do Japão, com registro de 5,8 graus na escala Richter.
Considere que m1 e m2 medem a energia liberada sob a forma de ondas que se propagam pela crosta terrestre por terremotos com registros, na escala Richter, r1 e r2, respectivamente.
Sabe-se que estes valores estão relacionados pela fórmula:
r1 – r2 = log10 (m1/m2)
Considerando-se que r1 seja o registro do terremoto da Turquia e r2 o registro do terremoto do Japão, pode-se afirmar que (m1/m2) é igual a:
a) 10–1 d) 10/0,1
b)  e) 1/0,1
e) 1/0,1
c) (0,1)10
Solução:
r1 – r2 = log10 (m1/m2) 
5,9 – 5,8 = log10 (m1/m2)

Resposta: B
34. (UnB-DF) A escala de um aparelho para medir ruídos é definida da seguinte forma: R = 12 + log10(I), em que R é a medida do ruído, em bels, e I é a intensidade sonora, em W/m2. No Brasil, a unidade utilizada é o decibel (1/10 do bel). Por exemplo, o ruído dos motores de um avião a jato é de 160 decibéis, enquanto o ruído do tráfego em uma esquina movimentada de uma grande cidade é de 80 decibéis, sendo este o limite a partir do qual o ruído passa a ser nocivo ao ouvido humano. Com base nessas informações, julgue os itens que se seguem.
(1) A intensidade sonora de um ruído de zero decibel é de 10–12 W/m2.
(2) A intensidade sonora dos motores de um avião a jato é o dobro da intensidade sonora do tráfego em uma esquina movimentada de uma grande cidade.
(3) Uma intensidade sonora maior que 10–4 W/m2 produz um ruído que é nocivo ao ouvido humano.
Solução:
(1) 0 = 12 + log10 (I)  log10 (I) = –12
log10 (I) = –12 
(2) Para o motor de um avião a jato, temos:
16 = 12 + log10 (Ij)  log10 (Ij) = 4
log10 (Ij) = 4  Ij= 104
Ij= 104
Para o tráfego em uma esquina movimentada, temos:
8 = 12 + log10 (Ie)  log10 (Ie) = –4
log10 (Ie) = –4  Ie = 10–4
Ie = 10–4
Logo Ij = 104  2 · Ie = 2 · 10–4 (Falsa)
2 · Ie = 2 · 10–4 (Falsa)
(3) Se 80 decibéis é o limite a partir do qual o ruído é nocivo ao ouvido humano, então:
8 = 12 + log10 (IL)  IL = 10–4 W/m2 (Verdadeira)
IL = 10–4 W/m2 (Verdadeira)
Resposta
(1) V (2) F (3) V
Solução: usando as propriedades do logaritmo, podemos reescrever a equação acima da seguinte forma:
Note que para isso utilizamos as seguintes propriedades:
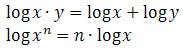
Vamos retornar à equação:
Como ficamos com uma igualdade entre dois logaritmos, segue que:
(2x +3)(x + 2) = x2
ou
2x2 + 4x + 3x + 6 = x2
2x2 – x2 + 7x + 6 = 0
x2 + 7x + 6 = 0
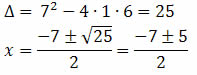
x = -1 ou x = - 6
Lembre-se que para o logaritmo existir o logaritmando e a base devem ser positivos.
Com os valores encontrados para x, o logaritmando ficará negativo. Sendo assim, a equação não tem solução ou S = ø.
36. (FUVEST-SP) Encontre a solução da equação
Solução:CE: Como a incógnita x não está presente no logaritmando nem na base do logaritmo, não há restrições para o valor de x. Portanto, x E R.
Eliminado o parênteses temos:
Usando as propriedades dos logaritmos:
Como não há restrições para o valor de x temos: S = {-2, 0}.
37. Resolva o sistema 
Solução:Condição de existência: x > 0 e y > 0
Na primeira equação temos: log x + log y = 7 => log y = 7 – log x
Substituindo log y na segunda equação temos:
3.log x–2.(7–log x) =1 => 3.log x – 14 + 2.log x = 1
5.log x = 15 =>log x = 3 => x=103³
Como x = 10³ e log y = 7 – log x, então:
7 – log x = 7 – log 103 => log y = 7 – 3 => log y = 4 => y = 104.
Como satisfazem à CE, temos:
38. (Fuvest-SP / Adaptada) Encontre o valor de x em 
Solução:Usando a propriedade do logaritmo da potência ao inverso temos:
39. Determine a solução (x,y, y > 1), para o sistema de equações:
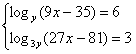
Solução:
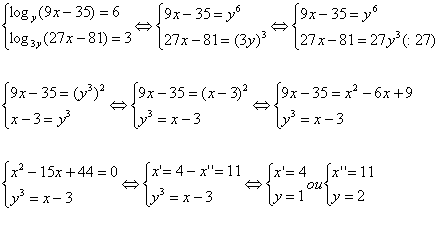
A condição é para y > 1, então, o conjunto solução é dado por x = 11 e y = 23.
Parabéns pelo site, muito bom!
ResponderExcluirMt bom, bem complementado
ResponderExcluirMt bom, bem complementado
ResponderExcluir