1) Para esvaziar um compartimento com 700m3 de capacidade, 3 ralos levaram 7 horas para fazê-lo. Se o compartimento tivesse 500m3 de capacidade, ao utilizarmos 5 ralos quantas horas seriam necessárias para esvaziá-lo?
Primeiramente atribuamos uma letra a cada grandeza:
- M: A capacidade em metros cúbicos do compartimento;
- R: A quantidade de ralos;
- H: A duração da operação de esvaziamento em horas.
A representação para a análise do problema, obtida segundo os dados do enunciado é a seguinte:
Observe que na montagem a grandeza que estamos procurando (H), está posicionada à direita (poderia estar à esquerda), o que facilmente nos permitirá deixar a razão com o termo x isolada.
Agora vamos determinar se as grandezas são diretamente ou inversamente proporcionais em relação à grandezaH. Para isto utilizaremos setas com a mesma orientação para indicar grandezas diretamente proporcionais e com orientação inversa para indicar o oposto.
Vamos arbitrar que a orientação da grandeza H seja para baixo:
Agora vejamos se H e M são diretamente proporcionais ou não. Sabemos que ao diminuirmos a capacidade do compartimento, também iremos diminuir o tempo necessário para esvaziá-lo, então logicamente as duas grandezas são diretamente proporcionais, então a seta de M terá a mesma orientação da seta de H que é para baixo:
Determinemos se R e H são diretamente ou inversamente proporcionais. Ao aumentarmos a quantidade de ralos, automaticamente iremos diminuir o tempo necessário para esvaziar o compartimento, isto indica que as duas grandezas são inversamente proporcionais, então a seta de R será orientada para cima, direção oposta a da seta de H:
Agora devemos deixar todas as grandezas com a mesma orientação. Neste caso somente a grandeza R possui orientação oposta à da grandeza H e por isto somente ela será invertida, tanto a seta, quanto os seus elementos:
Por último podemos montar a proporção e resolvê-la:
Portanto com 5 ralos poderíamos esvaziar 500m3 em três horas.
2) Duas costureiras trabalhando 3 dias, 8 horas por dia, produzem 10 vestidos. Se 3 costureiras trabalharem por 5 dias, quantas horas ela precisarão trabalhar por dia para produzirem 25 vestidos?
Vamos atribuir uma letra a cada grandeza:
- C: O número de costureiras;
- D: O número de dias de trabalho;
- J: A jornada de trabalho diária;
- P: A produção de vestidos.
Segundo os dados do enunciado a representação para a análise do problema é a seguinte:
Note que na montagem a grandeza J foi posicionada à direita para que facilmente possamos isolá-la no último passo.
Agora vamos determinar se as grandezas são diretamente ou inversamente proporcionais em relação à grandezaJ. Para isto utilizaremos setas com a mesma orientação para indicar grandezas diretamente proporcionais e com orientação inversa para indicar o oposto.
Segundo a lógica da orientação das setas, vamos arbitrar que a orientação da grandeza J seja para baixo para começarmos a análise:
C é inversamente proporcional a J, pois se aumentando o número de costureiras pode-se diminuir a jornada de trabalho para uma mesma produção:
D é inversamente proporcional a J, já que se aumentando o número de dias de trabalho pode-se diminuir a jornada de trabalho para uma mesma produção:
P é diretamente proporcional a J, já que se aumentarmos a produção de vestidos, teremos que aumentar a jornada de trabalho para um mesmo número de costureiras e dias de trabalho:
Deixemos agora todas as grandezas com a mesma orientação. As grandezas C e D são inversamente proporcionais à J, por isto as duas serão invertidas:
Montemos finalmente a proporção para a resolução do problema:
3) Cinco dias do trabalho de 3 costureiras podem render 25 vestidos sem que se altere a jornada diária de trabalho, ou seja, elas ainda continuarão a trabalhar 8 horas por dia.
Um automóvel percorre um espaço de 480 Km em 02 horas. Quantos kms ele percorrerá em 06 horas?
Grandeza 1: Distância percorrida
Cálculo:
Distância 1 = 480 Km - 02 horas
Distância 2 = ? Km - 06 horas
01 hora percorrida = 240 km
06 horas percorrida = 240 Km x 6
Resultado: 1440 Kms
Método mais prático de solução da regra de três simples
Faça um X na equação, pegue o primeiro número de cima (480) e multiplique pelo segundo número de baixo (06) depois é só dividir pelo número que restou (02) - O que você deseja saber está em Km, portanto a resposta será em Km
480 km - 02 horas
X
? km - 06 horas
Resp: ? = 480 . 06 / 02 = 1440 Km
4) Se 10 carros consomem em 05 dias a quantidade de 1000 litros de gasolina, quantos carros usaremos para consumir somente 500 litros de gasolina no espaço de 02 dias??
Grandeza 1: Número de carros
Grandeza 2: Número de dias
Grandeza 3: Quantidade combustível
Método mais prático de solução da regra de três composta
Faça a comparação da grandeza que irá determinar com as demais grandezas. Se esta grandeza for inversa, invertemos os dados dessa grandeza das demais grandezas.
A grandeza a se determinar não se altera, então, igualamos a razão das grandezas e determinamos o valor que se procura.
Veja:
Na alimentação de 02 bois, durante 08 dias, são consumidos 2420 kgs de ração. Se mais 02 bois são comprados, quantos quilos de ração serão necessários para alimentá-los durante 12 dias.
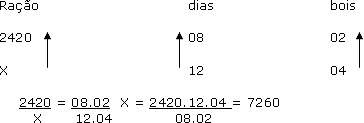
Assim: serão necessários 7260 Kgs de ração
5) Se 10 metros de um tecido custam R$ 50,00, quanto custará 22 metros ?
Solução: O problema envolve duas grandezas (quantidade de tecidos e preço da compra)
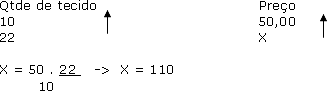
Assim: 22 metros custarão R$ 110,00
6) Em 06 dias de trabalho, 12 confeiteiros fazem 960 tortas. Em quantos dias 04 confeiteiros poderão fazer 320 tortas
Solução: O problema envolve três grandezas (tempo, número de confeiteiros, quantidade de tortas)
7) (UFRGS-RS) Se foram empregados 4 kg de fios para tecer 14 m de uma maquete de fazenda com 80 cm de largura, quantos quilogramas serão necessários para produzir 350 m de uma maquete de fazenda com 120 cm largura?
.gif)
Serão necessários 150 kg de fios para produzir uma maquete de fazenda de 350 m com 120 cm de largura.
8) (Unifor–CE) Um texto ocupa 6 páginas de 45 linhas cada uma, com 80 letras (ou espaços) em cada linha. Para torná-lo mais legível, diminui-se para 30 o número de linhas por página e para 40 o número de letras (ou espaços) por linha. Considerando as novas condições, determine o número de páginas ocupadas.

O número de páginas a serem ocupadas pelo texto respeitando as novas condições é igual a 18.
9) Um navio partiu do porto do Itaqui para uma viagem em alto mar levando a bordo reservas suficientes para alimentar seus 20 tripulantes durante 30 dias. Logo após a partida do navio, percebeu-se a presença de 4 tripulantes clandestinos. Nessas condições, quantos dias ainda vão durar as reservas de alimentos?
Note que se aumentarmos o número de tripulantes (no caso, 20 + 4), as reservas de alimento (x) diminuem. Portanto, são grandezas inversamente proporcionais (IP). Quando temos grandezas IP, a regra é a seguinte: a razão entre dois valores de uma é igual ao inverso da razão entre os dois valores correspondentes na outra. Então nossa proporção fica assim:
Em toda proporção, o produto dos meios é igual ao produto dos extremos, portanto
Logo, as reservas de alimentos vão durar 25 dias.
10) Trabalhando 8 horas por dia, durante 14 dias, Maurício recebeu R$ 2.100,00. Se trabalhar 6 horas por dia, durante quantos dias ele deve trabalhar para receber R$ 2 700,00?
h/d
|
Dias
|
R$
|
8
|
14
|
2100
|
6
|
x
|
2700
|
.jpg)
Ele deverá trabalhar 24 dias.
EXERCÍCIOS PROPOSTOS
1) (UFRGS-RS)
Se foram empregados 4 kg de fios para tecer 14 m de uma maquete de fazenda com 80 cm de largura, quantos quilogramas serão necessários para produzir 350 m de uma maquete de fazenda com 120 cm largura?
2) (UFMG)
Uma empresa tem 750 empregados e comprou marmitas individuais congeladas suficientes para o almoço deles durante 25 dias. Se essa empresa tivesse mais 500 empregados, a quantidade de marmitas adquiridas seria suficiente para quantos dias?
3) (Unifor–CE)
Um texto ocupa 6 páginas de 45 linhas cada uma, com 80 letras (ou espaços) em cada linha. Para torná-lo mais legível, diminui-se para 30 o número de linhas por página e para 40 o número de letras (ou espaços) por linha. Considerando as novas condições, determine o número de páginas ocupadas.
4) (Unifor–CE)
Se 6 impressoras iguais produzem 1000 panfletos em 40 minutos, em quanto tempo 3 dessas impressoras produziriam 2000 desses panfletos?
a) 4 gatos b) 3 gatos c) 2 gatos
d) 5 gatos e) 6 gatos
7) Com 50 kg de milho, obtemos 35 kg de fubá. Quantas sacas de 60 kg de fubá podemos obter com 1 200 kg de milho ?
8) Sete litros de leite dão 1,5 quilos de manteiga. Quantos litros de leite serão necessários para se obterem 9 quilos de manteiga ?
9) Em um banco, contatou-se que um caixa leva, em média, 5 minutos para atender 3 clientes. Qual é o tempo que esse caixa vai levar para atender 36 clientes ?
10) Paguei R$ 6,00 por 1.250 kg de uma substância. Quanto pagaria por 0,750 kg dessa mesma substância ?
GABARITO:
1) 150kg 2)15 dias 3) 18 paginas 4)160 minutos 5)A 6) 40kg 7) 14 sacas 8) 42 litros 9) 60 minutos 10) R$ 3,60
Fontes: matematicadidatica.com.br
brasilescola.com

Muito obrigada pela resolução passa a passo. Continue postando materiais assim...ajuda muito!
ResponderExcluirParabéns pelo espaço!!!
Ótimo, obrigada! Continue explicando passo a passo , trazendo imagens para facilitar a visualização,ajuda bastante. ;)
ResponderExcluirNossa !!! Que Alegria poder encontrar uma EXPLICAÇÃO ASSIM aqui neste site de vcs ok. Me ajudou bastante, pois eu já NÃO TINHA MAIS OS MEUS CADERNOS GUARDADOS, explicando Passo à Passo ESTA MATÉRIA. MUITÍSSIMO OBRIGADA pela A Grande Ajuda.
ResponderExcluirMuito BEM EXPLICADO MESMO, O Meu Muito obrigada mais uma vez. Se puderem continuem fazendo estas Postagens.
ResponderExcluirEssa das LETRAS E PAGINAS realmente é uma complicação para entender. Eu faço porque já vi a resolução varias vezes, mas ENTENDER mesmo (como tirar mais letras vai resultar em MAIS paginasw?????) é impossivel.
ResponderExcluirNão consigo chegar nesse entendimento!
:P
Ótimo passo a passo
ResponderExcluir