Artigo com questões resolvidas de vestibulares sobre dilatação linear, dilatação superficial e volumétrica
1) (UFPE) - O gráfico abaixo representa a variação, em milímetros, do comprimento de uma barra metálica, de tamanho inicial igual a 1,000m, aquecida em um forno industrial. Qual é o valor do coeficiente de dilatação térmica linear do material de que é feita a barra, em unidades de 10-6 ºC-1.
1) (UFPE) - O gráfico abaixo representa a variação, em milímetros, do comprimento de uma barra metálica, de tamanho inicial igual a 1,000m, aquecida em um forno industrial. Qual é o valor do coeficiente de dilatação térmica linear do material de que é feita a barra, em unidades de 10-6 ºC-1.
 | RESOLUÇÃO: ΔL = L0 . α . Δθ 15 = 1000 . α . (500 - 0) α = 30. 10-6 ºC-1 |
RESPOSTA: 30
2) Os componentes de uma lâmina bimetálica são o aço e o zinco. Os coeficientes de dilatação linear desses metais são, respectivamente, 1,2 . 10-5 °C-1 e 2,6 . 10-5 °C-1. Em uma determinada temperatura, a lâmina apresenta-se retilínea. Quando aquecida ou resfriada, ela apresenta uma curvatura. Explique por quê.
RESOLUÇÃO
Como αzinco > αaço, para um mesmo aumento de temperatura o zinco sofre uma dilatação maior, fazendo com que na lâmina ocorra uma dilatação desigual, produzindo o encurvamento. Como a dilatação do zinco é maior, ele ficará na parte externa da curvatura. No resfriamento, os metais se contraem. O zinco, por ter g maior, sofre maior contração. Assim, a parte de aço ocupa a parte externa da curvatura.

3) (VUNESP-SP) A dilatação térmica dos sólidos é um fenômeno importante em diversas aplicações de engenharia, como construções de pontes, prédios e estradas de ferro. Considere o caso dos trilhos de trem serem de aço, cujo coeficiente de dilatação é α = 11 . 10-6 °C-1. Se a 10°C o comprimento de um trilho é de 30m, de quanto aumentaria o seu comprimento se a temperatura aumentasse para 40°C?
a) 11 . 10-4 m
b) 33 . 10-4 m
c) 99 . 10-4 m
d) 132 . 10-4 m
e) 165 . 10-4 m
RESOLUÇÃO:
O cálculo da dilatação linear ΔL, do trilho é:
ΔL = L0 . α . Δθ
ΔL = 30 . (11 . 10-6) . (40 – 10) = 99 . 10-4 m
RESPOSTA: C
4) Uma placa apresenta inicialmente uma área de 1,0 m2 a 0°C. Ao ser aquecida até 50°C, sua área aumenta 1,0 cm2. Determine o coeficiente de dilatação superficial do material que constitui a placa.
Resolução:

5) Em uma placa de cobre existe um furo circular que, a 20°C, apresenta área igual a 200 mm2. Qual o acréscimo de área que o furo sofre quando se eleva a temperatura da chapa para 220°C?
Dado: coeficiente de dilatação superficial,
Resolução

6) Uma barra metálica tem, a 30°C, comprimento igual a 1m. Eleva-se então sua temperatura para 1030°C. Sendo o coeficiente de dilatação linear do metal da barra igual a 12 · 10-6 °C-1, determine a variação de comprimento sofrida pela barra.
Resolução

7) Um trilho de ferro com 20 m de comprimento a 10°C é aquecido até atingir 110°C, sofrendo um acréscimo de 2,2 cm em seu comprimento. Qual é o valor do coeficiente de dilatação linear do ferro?
Resolução

8) Uma estatueta de ouro foi aquecida de 25°C a 75°C, observando-se um aumento de 2,1 cm3 em seu volume. Sendo 14 · 10 –6 °C–1 o coeficiente de dilatação linear do ouro, qual era o volume inicial dessa estatueta?
Resolução

9) Um recipiente de cobre tem 1 000 cm3 de capacidade a 0 °C. Sua capacidade, a 100 °C, vale aproximadamente:
a) 1 017 cm3
b) 1 005 cm3
c) 1 003 cm3
d) 1 002 cm3
e) 1 001 cm3
Dado: coeficiente de dilatação linear do
cobre = 16 · 10–6 °C–1
Resolução

10) Qual o coeficiente de dilatação volumétrica de uma barra metálica que experimenta um aumento de 0,1% em seu comprimento para uma variação de temperatura de 100 °C?
Resolução

11) Sabe-se que o coeficiente de dilatação real do mercúrio vale 18 · 10–5 °C–1. Qual é o coeficiente de dilatação aparente do mercúrio, quando medido num recipiente de alumínio?
Dado: coeficiente de dilatação linear do
alumínio = 24 · 10–6 °C–1
Resolução

12) Um recipiente de cobre, de coeficiente de dilatação volumétrico médio  frasco = 51 · 10–6 °C–1, contém mercúrio, a 0 °C, até o volume de 45 cm3. O volume do recipiente a 0 °C é de 46 cm3. Considere o coeficiente de dilatação do mercúrio
frasco = 51 · 10–6 °C–1, contém mercúrio, a 0 °C, até o volume de 45 cm3. O volume do recipiente a 0 °C é de 46 cm3. Considere o coeficiente de dilatação do mercúrio  Hg = 180 · 10–6°C–1. A que temperatura o mercúrio encherá completa- mente o recipiente?
Hg = 180 · 10–6°C–1. A que temperatura o mercúrio encherá completa- mente o recipiente?
Resolução

Para o mercúrio preencher todo o recipiente ele deve sofrer uma dilatação aparente de 1,0 cm3:



13) O coeficiente de dilatação superficial de certo material homogêneo e isótropo é 3,68 · 10–5 °C–1. Determine os seus coeficientes de dilatação linear e volumétrico.
Resolução
Temos em:
Substituindo vem:
14) .Um certo frasco de vidro está completamente cheio, com 50 cm3 de mercúrio. O conjunto se encontra inicialmente a 28 °C. No caso, o coeficiente de dilatação médio do mercúrio tem um valor igual a 180 · 10–6 °C–1 e o coeficiente de dilatação linear médio do vidro vale 9 · 10–6 °C–1. Determine o volume de mercúrio extravasado, quando a temperatura do conjunto se eleva para 48 °C.
Resolução
O volume de líquido extravasado correspondente ao volume do líquido transbordado (aparente).

Resolução

Volumes iguais no final

Observação: A dilatação volumétrica pode ser aplicada para qualquer forma de corpo (esférico, cúbico etc) e para corpos maciços ou ocos.
16) Um quadrado de lado 2m é feito de um material cujo coeficiente de dilatação superficial é igual a 1,6.10-4. Determine a variação de área deste quadrado quando aquecido em 80°C.
Resolução:
ΔA = Ao.β.Δ?
ΔA = 4. 1,6.10-4.80
ΔA = Ao.β.Δ?
ΔA = 0,0512m²
17) (UNIC –MT) Uma chapa de alumínio tem um furo central de 100cm de raio, estando numa temperatura de 12°C.

Sabendo-se que o coeficiente de dilatação linear do alumínio equivale a 22.10-6°C-1, a nova área do furo, quando a chapa for aquecida até 122°C, será equivalente a qual valor em metros?
Resolução:
A = Ao.(1 + β.Δ?)
A = ?.r²..(1 + β.Δ?)
A = ?.1².(1 + 44.10-6.110)
A = ?.(1 + 0,00484)
A = ?.(1,00484)
A = 3,155 em valor aproximado.
A = ?.r²..(1 + β.Δ?)
A = ?.1².(1 + 44.10-6.110)
A = ?.(1 + 0,00484)
A = ?.(1,00484)
A = 3,155 em valor aproximado.
18) Um fazendeiro quer cercar com arame um terreno quadrado de lados 25m e para isso adquire 100m de fio. Fazendo o cercado, o fazendeiro percebe que faltaram 2cm de fio para a cerca ficar perfeita. Como não quer desperdiçar o material e seria impossível uma emenda no arame, o fazendeiro decide pensar em uma alternativa. Depois de algumas horas, ele percebe que naquele dia a temperatura da cidade está mais baixa do que a média e decide fazer cálculos para verificar se seria possível utilizar o fio num dia mais quente, já que ele estaria dilatado. Sabendo que o acréscimo no comprimento do fio é proporcional ao seu comprimento inicial, ao seu coeficiente de dilatação linear e à variação de temperatura sofrida, calcule o aumento de temperatura que deve ocorrer na cidade para que o fio atinja o tamanho desejado. (Dado: coeficiente de dilatação térmica linear do fio =
Resolução:
Sendo a dilatação linear dada por:
Lembrando que as unidades de comprimento devem estar no mesmo sistema de unidades, a variação deve ser igual a 0,02m:
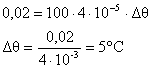
19) Duas barras de 3 metros de alumínio encontram-se separadas por 1cm à 20°C. Qual deve ser a temperatura para que elas se encostem, considerando que a única direção da dilatação acontecerá no sentido do encontro? Sendo 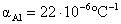 .
.
Resolução:
Sendo a dilatação linear dada por:
Mas a variação no comprimento das barras deve ser apenas 0,5cm = 0,005m, pois as duas barras variarão seu comprimento, então substituindo os valores:
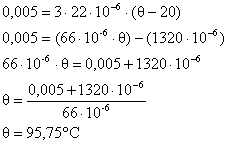
20) Um paralelepípedo de uma liga de alumínio (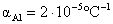 ) tem arestas que, à 0°C, medem 5 cm, 40 cm e 30 cm. De quanto aumenta seu volume ao ser aquecido à temperatura de 100°C?
) tem arestas que, à 0°C, medem 5 cm, 40 cm e 30 cm. De quanto aumenta seu volume ao ser aquecido à temperatura de 100°C?
Primeiramente deve-se calcular o volume do paralelepípedo à 0°C:
Resolução:
Sendo a dilatação volumétrica dada por:
Mas:
Substituindo os valores na equação:
21) Um recipiente de vidro. com a capacidade de 3000cm³, está completamente cheio com líquido, a 0°C. O conjunto é aquecido até 100°C e observa-se que 15cm³ desse líquido extravasa do recipiente.
Considerando-se o coeficiente de dilatação linear do vidro como sendo constante no referido intervalo térmico e igual a 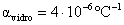 , qual o coeficiente de dilatação real desse líquido?
, qual o coeficiente de dilatação real desse líquido?
Resolução:
Sabendo que
E que:
De modo que podemos calcular o coeficiente de dilatação aparente do líquido e descobrir o coeficiente de dilatação real, ou seja:
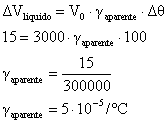
22) (MACKENZIE) Ao se aquecer de 1,0ºC uma haste metálica de 1,0m, o seu comprimento aumenta de 2,0 . 10-2mm. O aumento do comprimento de outra haste do mesmo metal, de medida inicial 80cm, quando a aquecemos de 20ºC, é:
a) 0,23mm
b) 0,32 mm
c) 0,56 mm
d) 0,65 mm
e) 0,76 mm
Resolução
ΔL = 2 . 10-2 mm = 2 . 10-2 . 10-3 m
L0 = 1 m
Δθ = 1 ºC
ΔL = L0αΔθ
α = ΔL/L0Δθ
α = 2 . 10-5 ºC-1
L0' = 80 cm = 80 . 10-2 m
Δθ' = 20 ºC
ΔL' = L0'αΔθ'
ΔL' = 80 . 10-2 . 2 . 10-5 . 20 = 3200 . 10-7 = 0,32 . 10-3 m = 0,32 mm
23) (UELON-PR) O volume de um bloco metálico sofre um aumento de 0,60% quando sua temperatura varia de 200ºC. O coeficiente de dilatação de dilatação linear médio desse metal, em ºC-1,vale:
a) 1,0.10-5
b) 3,0.10-5
c) 1,0.10-4
d) 3,0.10-4
e) 3,0.10-3
Resolução
ΔV = 0,006V0
Δθ = 200º C
ΔV = V0γΔθ
γ = ΔV/V0Δθ
γ = 0,006V0/V0200 = 0,00003
α = β/2 = γ/3
α = γ/3 = 0,00003/3 = 0,00001 = 1 . 10-5
24) Qual é o valor do coeficiente de dilatação linear de uma barra homogênea de:
Comprimento inicial: 2.00mComprimento final: 2.02m
Variação do comprimento (ΔL): 0,02m
Temperatura inicial: 0°c
Temperatura final: 200°c
Variação da temperatura (Δt): 200°c
Resolução:
a dilatação linear é dada por
ΔL= α Li ΔT
aonde
α = coeficiente de dilatação linear
ΔL = Lf - Li
Lf = comprimento final
Li = comprimento inicial
ΔT = Tf - Ti
Tf = temperatura final
Ti = temperatura inicial
Então usando os dados do enunciado
ΔL = Lf - Li = 2,02m - 2,00m= 0,02m
ΔT = Tf - Ti = 200°C - 0°C = 200°C
Assim
ΔL=α Li ΔT
se torna
0,02 = α (2,00) (200)
0,01 = α (200)
α = 0,00005 / °C ou
==================
α = 5 * 10^(-5) °C^(-1)
==================
a dilatação linear é dada por
ΔL= α Li ΔT
aonde
α = coeficiente de dilatação linear
ΔL = Lf - Li
Lf = comprimento final
Li = comprimento inicial
ΔT = Tf - Ti
Tf = temperatura final
Ti = temperatura inicial
Então usando os dados do enunciado
ΔL = Lf - Li = 2,02m - 2,00m= 0,02m
ΔT = Tf - Ti = 200°C - 0°C = 200°C
Assim
ΔL=α Li ΔT
se torna
0,02 = α (2,00) (200)
0,01 = α (200)
α = 0,00005 / °C ou
==================
α = 5 * 10^(-5) °C^(-1)
==================
25) Um anel de ferro com raio interno de 3 cm a 10 °C é aquecido até 110 °C. Seu coeficiente de dilatação térmica linear, nesse intervalo de temperatura, é igual a 12.10^-6 °C^-1. A variação de sua área interna, em cm², é aproximadamente de?
Resolução:
Usa que
ΔA = β A0 ΔT
aonde
ΔA é a variação da área do buraco. Isto mesmo! O buraco dilata-se como se fosse feito do mesmo material.
β é o coeficiente de dilatação térmica superficial. Mas β = 2α
sendo α o coeficiente de dilatação térmica linear, dado no enunciado.
A0 é a área inicial
ΔT é a variação da temperatura
Então
ΔA = 2α A0 ΔT
mas A0 = R²
aonde R =3 cm = 0,03 m
Então
ΔA = 2α πR² ΔT
ΔA = 2 * 12 * 10^-6 * π * (0,03)² (110-10)
ΔA ≈ 0,68 * 100 * 10^-6
ΔA ≈ 0,68 * 10^-4 m² = 0,68 cm²
Portanto
===========
ΔA = 0,68 cm²
===========
26) Um copo de vidro de capacidade 100cm³, a 20,0ºC contém 98,0 cm³ de mercúrio a essa temperatura. São dados os coeficientes de dilatação cúbica do mercúrio = 180x10-6 (cento e oitenta vezes dez elevado a menos seis) e vidro = 9x10-6 (nove vezes dez elevado a menos 6). A que temperatura o mercúrio começa a extravasar, em ºC, é mais próxima de:
Resolução:
líquido e recipiente irão se expandir mais o líquido por ter maior coeficiente de dilatação se expandirá mais. Líquido começa com volume menor do que cabe no recipiente. Então para algum valor de variaão de temperatura ΔT ambos terão o mesmo volume:
Vl = Vr
aonde Vl é o volume do líquido e Vr o volume de líquido que o recipiente pode conter.
Mas
Vf = V + ΔV
aonde V é o volume inicial, Vf o volume final e ΔV a quantidade que expandiu. Assim
Vl = Vr
Vl + ΔVl = Vr + ΔVr
Sabemos que
ΔV = γ V ΔT
aonde
γ é o coeficiente de dilatação volumétrica ou cúbica.
V é o volume inicial
ΔT é a variação de temperatura.
Assim
Vl + ΔVl = Vr + ΔVr
se torna
Vl + γl Vl ΔT = Vr + γr Vr ΔT
Vl + γl Vl (Tf - Ti) = Vr + γr Vr (Tf - Ti)
Organizando os termos
γl Vl Tf - γr Vr Tf = Vr - Vl + γl Vl Ti - γr Vr Ti
(γl Vl - γr Vr) Tf = Vr - Vl + (γl Vl - γr Vr) Ti
Então temos que
Tf = Ti + (Vr - Vl) /(γl Vl - γr Vr)
Usando os dados do enunciado
Tf = 20 + (100 - 98) /(180x10-6 x98 - 9x10-6 x100)
Tf = 20 + (2) /(17640 x10-6 - 900x10-6 )
Tf = 20 + (2) /(16740 x10-6 )
Tf = 20 + 2x10^6 /16740
Tf = 20 + 2 000 000 /16740
Como 2 000 000 /16740 ≈ 119,5
Tf ≈ 139,5 ºC
ou sem casas decimais:
=========
Tf ≈ 140 ºC
27) Um orificio circular numa placa de aço tem diametro de 10,000 cm à temperatura de 10 ºC. Se o coeficiente de dilatação linear do aço é de 11.10-6 ºC-1, o diâmetro desse orificio à temperatura de 110 ºC será, em centímetros, de:
a) 9,012 b) 10,011 c) 10,121 d) 11,011 e) 12,121
a) 9,012 b) 10,011 c) 10,121 d) 11,011 e) 12,121
Resolução:
Antes de mais nada, é necessário saber que qualquer material ao ter sua temperatura aumentada sofre uma dilatação ( aumento de suas dimensões ).
Analisa-se, então, um caso de dilatação linear onde uma barra metálica sofre um aumento de temperatura.
Após pesquisas realizadas em laboratórios constatou-se que a dilatação do comprimento de uma barra metálica depende de seu comprimento inicial, da variação de temperatura por ela sofrida e do coeficiente de dilatação térmica linear, este dependente do material de constituição da barra.
As dilatações superficiais (áreas) e volumétricas (volumes) seguem as mesmas regras. Apenas se considera no lugar dos comprimentos, áreas e volumes:
Muita atenção na hora de calcular as dilatações superficiais e volumétrias pois seus coeficientes de dilatações são o dobro e o triplo, respectivamente, do coeficiente de dilatação linear. Para se saber qual das dilatações esta ocorrendo basta perguntar: O que aumentou? O comprimento, a superfície ou o volume.
Neste problema, em específico, apesar de ocorrer um aumento na superfície pa chapa e, também, do furo a pergunta é qual o diâmetro final do furo, ou seja, de quanto aumento o diâmetro (comprimento dele). Tem-se, então, uma dilatação linear. Calcula-se:
Percebe-se que o diâmetro aumentou 0,011 cm, mas a pergunta é: Qual o diâmetro final?
28) (CGE 195) Uma barra de ferro homogênea possui, a 10 °C, o comprimento de 5 metros. Se o coeficiente de dilatação linear do ferro é ,
a temperatura a que esta barra deve ser aquecida para seu comprimento seja 5,003 m, é de:
a) 40 °C b) 50 °C c) 60 °C d) 83 °C e) 260 °C
Resolução:
O comprimento inicial da barra é 5 m e no final do processo passa para 5,003 m, então:
Seguindo o conceito de dilatação térmica linear, tem-se:
Percebe-se que a variação de temperatura foi de 50 °C, logo:
No final do processo a barra terá a temperatura de 60 °C, alternativa C.
29) A superfície de um corpo é dilatada ao ser aquecido. Calcule a dilatação desse corpo sabendo que o coeficiente de dilatação superficial é de 20µ °C-1, a superfície inicial é de 100 cm² e que a variação da temperatura foi de 130°C. µ = 10-6
Resolução:
O primeiro passo é anotar os dados.
ΔS = ?
ΔΘ = 130 °C
β = 20µ °C-1
Si = 100 cm²
Agora é só substituir na fórmula da dilatação superficial.
ΔS = Si x β x ΔΘ
ΔS = 100 x 20µ x 130
ΔS = 260000 µ
ΔS = 0,26 cm²
A superfície do corpo dilatou 0,26 cm².
ΔS = ?
ΔΘ = 130 °C
β = 20µ °C-1
Si = 100 cm²
Agora é só substituir na fórmula da dilatação superficial.
ΔS = Si x β x ΔΘ
ΔS = 100 x 20µ x 130
ΔS = 260000 µ
ΔS = 0,26 cm²
A superfície do corpo dilatou 0,26 cm².
30) Um corpo sofre dilatação ao ser aquecido e contrai ao ser resfriado. Um corpo foi resfriado, passando de 800 °C para 50 °C. A superfície inicial do corpo media 40 m² e o coeficiente de dilatação superficial do corpo é de 90µ °C-1. Calcule a variação da superfície do corpo. µ = 10-6
Resolução:
O primeiro passo é anotar os dados.
ΔS = ?
ΔΘ = 50 – 800 = -750 °C
β = 90µ °C-1
Si = 40 m²
Agora é só substituir na fórmula da dilatação superficial.
ΔS = Si x β x ΔΘ
ΔS = 40 x 90µ x (-750)
ΔS = -2700000 µ
ΔS = -2,7 m²
A superfície contraiu 2,7 m².
ΔΘ = 50 – 800 = -750 °C
β = 90µ °C-1
Si = 40 m²
Agora é só substituir na fórmula da dilatação superficial.
ΔS = Si x β x ΔΘ
ΔS = 40 x 90µ x (-750)
ΔS = -2700000 µ
ΔS = -2,7 m²
A superfície contraiu 2,7 m².
31) Um corpo com coeficiente de dilatação superficial de 25µ °C-1 deve ter sua superfície aumentada em 40%. Qual deve ser a variação de temperatura que o corpo deve ser submetido para que isto ocorra? µ = 10-6
Resolução:
O primeiro passo é anotar os dados.
ΔS = 40% de Si = 0,4 Si
ΔΘ = ?
β = 25µ °C-1
Si = Si cm²
Agora é só substituir na fórmula da dilatação superficial.
ΔS = Si x β x ΔΘ
0,4Si = Si x 25µ x ΔΘ
ΔΘ =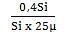
ΔS = 40% de Si = 0,4 Si
ΔΘ = ?
β = 25µ °C-1
Si = Si cm²
Agora é só substituir na fórmula da dilatação superficial.
ΔS = Si x β x ΔΘ
0,4Si = Si x 25µ x ΔΘ
ΔΘ =
ΔΘ = 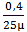
ΔΘ = 16000 °C
A temperatura deve ser aumentada 16000 °C.
ΔΘ = 16000 °C
A temperatura deve ser aumentada 16000 °C.
32) (OSEC-SP) Uma chapa metálica sofre um aumento de área de 0,06% ao ser aquecida de 100 ºC. Calcule o coeficiente de dilatação linear desse material, em ºC-1. (resp.: 3.10-5ºC-1)
Resolução:
Coeficiente de dilatação superficial = CS
Coeficiente de dilatação linear = CL
CS = 2. CL
Temos:
DeltaA = Ao . CS . DeltaTeta.
6 . 10^-4 . Ao = Ao . CL . 100
CS = 6 . 10^-5
CS = 2 CL
6 . 10^-5 = 2 CL
CL = 3 . 10^-5
Coeficiente de dilatação linear = CL
CS = 2. CL
Temos:
DeltaA = Ao . CS . DeltaTeta.
6 . 10^-4 . Ao = Ao . CL . 100
CS = 6 . 10^-5
CS = 2 CL
6 . 10^-5 = 2 CL
CL = 3 . 10^-5
33) Uma placa retangular de alumínio tem 10cm de largura e 40cm de comprimento, à temperatura de 20ºC. Essa placa é colocada num ambiente cuja temperatura é de 50ºC. Sabendo que al = 46.10-6 °C-1, calcule:
al = 46.10-6 °C-1, calcule:
a) A dilatação superficial da placa.
b) A área da placa nesse ambiente.
Resolução:
a) Cálculo da área inicial:
Si = 10 . 40 = 400cm2
Calculo da dilatação superficial:
S = 0,522cm2
b) Sf = Si + S
Sf = 400,552cm2 .
34) A área de uma chapa quadrada varia de 0,14 cm2 quando submetida a uma variação de 100 0C na sua temperatura. Sendo a aresta do quadrado inicial de 10 cm determine o coeficiente de dilatação linear (α) do material que constitui a chapa.
Resolução
Dados: ∆S = 0,14 cm2
∆t = 100 0C
S0 = a
a = 10 cm x 10 cm =100 cm2.
∆S = S0 . β . ∆t
0,14 = 100.β . 100
β = 14. 10-6 0C-1
O coeficiente de dilação superficial é igual ao coeficiente de dilatação linear dividido por dois. Logo,
β = 2.α
α = β / 2
α = 7 . 10-6 0C-1
Resposta: α = 7.10-6 0C-1
25) O comprimento de uma barra é de 30,000 cm a 0 oC.
a) Qual será o aumento de comprimento ocorrido quando a temperatura se eleva para 100 oC.
b) Qual é o comprimento final da barra?
O coeficiente de dilatação do material é 25 . 10-6 oC-1.
a) ΔL = L0 . α . Δt
ΔL = 30,000 . 25 . 10-6 . 100
ΔL = 75. 10-3
ΔL = 0,075
b) ΔL = Lf – L0
Lf = L0 + ΔL
Lf = 30,000 + 0,075
Lf = 30,075 cm
Resposta:
a) ΔL = 0,075 cm
b) Lf = 30,075 cm
36) (FEI) Um recipiente, cujo volume é de 1000 cm3, a 0°C, contém 980 cm3 de um líquido à mesma temperatura. O conjunto é aquecido e, a partir de uma certa temperatura, o líquido começa a transbordar. Sabendo-se que o coeficiente de dilatação cúbica do recipiente vale 2,0 x 10-5 °C-1 e o do líquido vale 1,0 x 10-3 °C-1, pode-se afirmar que a temperatura no início do transbordamento do líquido é, aproximadamente:

a) Qual será o aumento de comprimento ocorrido quando a temperatura se eleva para 100 oC.
b) Qual é o comprimento final da barra?
O coeficiente de dilatação do material é 25 . 10-6 oC-1.
Resolução
a) ΔL = L0 . α . Δt
ΔL = 30,000 . 25 . 10-6 . 100
ΔL = 75. 10-3
ΔL = 0,075
b) ΔL = Lf – L0
Lf = L0 + ΔL
Lf = 30,000 + 0,075
Lf = 30,075 cm
Resposta:
a) ΔL = 0,075 cm
b) Lf = 30,075 cm
36) (FEI) Um recipiente, cujo volume é de 1000 cm3, a 0°C, contém 980 cm3 de um líquido à mesma temperatura. O conjunto é aquecido e, a partir de uma certa temperatura, o líquido começa a transbordar. Sabendo-se que o coeficiente de dilatação cúbica do recipiente vale 2,0 x 10-5 °C-1 e o do líquido vale 1,0 x 10-3 °C-1, pode-se afirmar que a temperatura no início do transbordamento do líquido é, aproximadamente:
a) 6,0°C
b) 12°C
c) 21°C
d) 78°C
e) 200°C
Resolução:

37) (ENEM-2009) Durante uma ação de fiscalização em postos de combustíveis, foi encontrado um mecanismo inusitado para enganar o consumidor. Durante o inverno, o responsável por um posto de combustível compra álcool por R$ 0,50 /litro, a uma temperatura de 5 °C. Para revender o líquido aos motoristas, instalou um mecanismo na bomba de combustível para aquecê-lo, para que atinja a temperatura de 35 °C, sendo o litro de álcool revendido a R$ 1,60. Diariamente o posto compra 20 mil litros de álcool a 5 °C e os revende. Com relação à situação hipotética descrita no texto e dado que o coeficiente de dilatação volumétrica do álcool é de 1 × 10-3 °C-1 , desprezando-se o custo da energia gasta no aquecimento do combustível, o ganho financeiro que o dono do posto teria obtido devido ao aquecimento do álcool após uma semana de vendas estaria entre





 Substituindo as áreas (A) por (
Substituindo as áreas (A) por ( ), onde quadrado e lado vez lado.
), onde quadrado e lado vez lado.
 Assim podemos analisar a equação térmica do bloco 2:
Assim podemos analisar a equação térmica do bloco 2:


a) 10,1
b) 10,2
c) 10,3
d) 10,6
e) 11,2
54) (UDESC) Um recipiente para líquidos com capacidade para 120 litros, é completamente cheio a uma temperatura de 10°C. Esse recipiente é levado para um local onde a temperatura é de 30°C. Sendo o coeficiente de dilatação volumétrica do líquido igual a 1,2 x 10-3 (°C)-1, e considerando desprezível a variação de volume do recipiente, a quantidade de líquido derramado em litros é:
a) 0,024
b) 0,24
c) 2,88
d) 4,32
e) 5,76
a) 270mm
b) 257mm
c) 285mm
d) 300mm
e) 540mm
a) a perda de calor por radiação é grande;
b) o coeficiente de dilatação da água é constante no intervalo de 0°C a 100°C;
c) o coeficiente de dilatação da água entre 0°C e 4°C é negativo;
d) o calor específico do vidro é maior que o da água;
e) há necessidade de um tubo capilar de altura aproximadamente 13 vezes maior do que o exigido pelo mercúrio.
A) R$500,00 e R$1.000,00.
B) R$1.050,00 e R$1.250,00.
C) R$4.000,00 e R$5.000,00.
D) R$6.000,00 e R$6.900,00.
E) R$7.000,00 e R$7.950,00.
Resolução
ΔV = . V0 . Δt = 20 x 103 x 1 x 10-3 x 30 = 600 litros
Em 1 semana, o ganho em volume será de 600 x 7 = 4 200 litros
Se o litro for vendido a R$ 1,60, o ganho seá de 4 200 x 1,60 =
= R$ 6720,00
38) Um vendedor de gasolina recebe em seu tanque 2000L de gasolina á temperatura de 30ºC. Sabendo-se que posteriormente vendeu toda a gasolina quando a temperatura era de 20°C e que o coeficiente de dilatação da gasolina é igual a 1,1.10-³ °C-¹, qual o prejuízo que sofreu o vendedor?
Resolução:
Como a temperatura final é menor que a inicial, a variação fica negativa, temos então:
ΔV = VoYΔT
ΔV = VoY(Tf – To)
ΔV = VoYΔT
ΔV = VoY(Tf – To)
ΔV = 2*10³ * 1,1*10 – ³*(20 – 30)
ΔV = 2*10³ * 1,1*10 – ³ * -10
ΔV = – 22 litros
Não estranhe pelo fato da resposta ter dado negativa, pois a própria resposta só está indicando a perda de combustível, o prejuízo sofrido.
ΔV = – 22 litros
Não estranhe pelo fato da resposta ter dado negativa, pois a própria resposta só está indicando a perda de combustível, o prejuízo sofrido.
39) Uma Chapa plana de uma liga metálica tem coeficiente de dilatação linear 2. 10-5 tem área Ao á temperatura de 20°C. Para que a área dessa placa aumente 1%,devemos elevar sua temperatura para:
Resolução:
Acompanhe o raciocínio:
Ao ————— 100%
x —————- 1%
x=Ao/100
Agora o x é a variação de área. Agora ficou fácil. Basta aplicarmos na formula, sabendo que B=2a que é igual a 4*10-5:
ΔA=Ao*B*ΔT
Ao/100=Ao*4*10-5*ΔT
1/100=4*10-5ΔT
0,01/4*10-5ΔT
ΔT=250°C
Mas ΔT é igual a:
ΔT=Tf -To
Sendo ΔT=250°C, temos:
Ao ————— 100%
x —————- 1%
x=Ao/100
Agora o x é a variação de área. Agora ficou fácil. Basta aplicarmos na formula, sabendo que B=2a que é igual a 4*10-5:
ΔA=Ao*B*ΔT
Ao/100=Ao*4*10-5*ΔT
1/100=4*10-5ΔT
0,01/4*10-5ΔT
ΔT=250°C
Mas ΔT é igual a:
ΔT=Tf -To
Sendo ΔT=250°C, temos:
250=Tf -20
Tf=270°C
Tf=270°C
40) Um trilho de aço tem 10m de comprimento a – 10°C. Suponha que a temperatura suba para 40°C e que o coeficiente de dilatação do aço seja exatamente 12*10° -6 °C -1. Qual é o acréscimo e o comprimento final do trilho?
Resolução:
Bem, para sabermos a variação de comprimento basta aplicarmos na fórmula de dilatação térmica para a variação do comprimento. Assim:
ΔL = Lo*a*ΔT
ΔL = Lo*a*(T – To)
ΔL = 10 * 12*10-6 * [40 - (-10)]
ΔL = 120*10-6 * (40 + 10)
ΔL = 120*10-6 * 50
ΔL = 6000*10-6
ΔL = 0,006 m
Agora para saber o comprimento final é fácil. Sabe-se que ΔL é igual a:
ΔL = L – Lo
L = ΔL + Lo
L = 0,006 + 10
L = 10,006m
ΔL = Lo*a*ΔT
ΔL = Lo*a*(T – To)
ΔL = 10 * 12*10-6 * [40 - (-10)]
ΔL = 120*10-6 * (40 + 10)
ΔL = 120*10-6 * 50
ΔL = 6000*10-6
ΔL = 0,006 m
Agora para saber o comprimento final é fácil. Sabe-se que ΔL é igual a:
ΔL = L – Lo
L = ΔL + Lo
L = 0,006 + 10
L = 10,006m
41) Duas barras metálicas, de diferentes materiais, apresentam o mesmo comprimento a 0° C. Ao serem aquecidas, à temperatura de 100° C, a diferença entre seus comprimentos passa a ser de 1 mm. Sendo 2,2 . 10–5 °C–1 o coeficiente de dilatação linear do material de uma barra e 1,7 . 10–5 °C–1 o do material da outra, o comprimento dessas barras a 0 °C era:
a) 0,2 b) 0,8 c) 1,0 d) 1,5 e) 2,0
a) 0,2 b) 0,8 c) 1,0 d) 1,5 e) 2,0
Resolução:
Vamos descobrir o comprimento de cada barra com essa variação de 100°C (ΔT = 100 – 0 = 100°C). Lembre-se que o comprimento das barras era o mesmo inicialmente (Lo). Assim:
L1 = Lo(1 + α1ΔT)
L1 = Lo(1 + 1,7*10-5*100)
L1 = Lo(1 + 170*10-5)
L1 = Lo(1 + 0,00170)
L1 = Lo(1,0017)
L1 = 1,0017Lo (I)
Para a segunda barra, temos:
L2 = Lo(1 + α2ΔT)
L2 = Lo(1 + 2,2*10-5*100)
L2 = Lo(1 + 220*10-5)
L2 = Lo(1 + 0,0022)
L2 = 1,0022Lo (II)
Subtraindo as equações (II) e (I), temos:
L2 – L1 = 1,0022Lo – 1,0017Lo
L2 – L1 = 0,0005Lo
L2 – L1 = 5*10-4Lo
Mas a questão afirmou que a diferença de seus comprimentos ao serem aquecidas é 1mm = 1*10-³ m, ou seja, L2 – L1 = 1*10-³. Assim:
1*10-³ = 5*10-4Lo
Lo = 1*10-³ / 5*10-4
Lo = 0,2*10¹
Lo = 2,0 m
Portanto, a alternativa correta é E.
42) Um bloco metálico é aquecido de 20 ºC a 120 ºC e seu volume sofre um acréscimo de 3%. Qual é o coeficiente de dilatação linear do material que constitui o bloco?
Resolução:
ΔV/V0 = γ.Δθ => 3/100 = 3.α.(120-20) => α = 10-4 ºC-1
Resposta: 10-4 ºC-1
Resposta: 10-4 ºC-1
43) Uma garrafa térmica contém 130 cm3 de café quente, à temperatura de 80 C. Nela, você põe uma pedra de gelo de 12 g, em seu ponto de fusão, para esfriar o café. Quantos graus o café esfria, após o gelo ter derretido? Trate o café como se fosse da água pura.




Se considerar a garrafa como um sistema isolado, dessa forma não haverá perda de energia. Assim o calor cedido pelo café  (alumínio) mais o calor cedido pelo
(alumínio) mais o calor cedido pelo  (gelo)para derreter e aquecer deve ser nulo:
(gelo)para derreter e aquecer deve ser nulo:
Considerando que a conservação de energia nos diz que num sistema fechado Q=0 e  . Nos da que
. Nos da que  +
+ =0.
=0.
Já na capacidade calorífica temas as Eq:  onde
onde  +
+ =0.
=0.
As letras (g e a) estão relacionadas com a água e o gelo,  e o calor latente de fusão do gelo. Para se calcular a massa do café usasse a Eq:
e o calor latente de fusão do gelo. Para se calcular a massa do café usasse a Eq: 
Como a densidade do café e um 1,00g/ cm3 a 20C, volume do café aproximadamente de 2 cm3 volume do café a 20C  vale:
vale: 
Combinando (1) e (2) nos da:
Substituindo valores na Eq:

Logo T será 
44) A figura a seguir mostra uma esfera de aço de 50,1 mm de diâmetro apoiada num anel de alumínio, cujo diâmetro interno é de 50,0 mm, ambos à mesma temperatura. Qual o acréscimo de temperatura que esse conjunto deve sofrer para que a esfera passe pelo anel?
(Dados: α aço = 1,08. 10-5 °C-1 e α al = 2,38 . 10-5 °C-1)

Resolução:
Devemos admitir que quando a esfera passa pelo anel, o diâmetro da esfera de aço (L aço ) é igual ao diâmetro interno do anel de alumínio (L al ). Portanto, basta determinar o valor de ∆T para que essa igualdade ocorra.
Assim, da expressão L = Lo + ∆L, podemos fazer:
L aço = L al → Lo aço + ∆L aço = Lo al + ∆L al → ∆L al - ∆L aço = Lo aço - Lo al (1)
Assim, da expressão L = Lo + ∆L, podemos fazer:
L aço = L al → Lo aço + ∆L aço = Lo al + ∆L al → ∆L al - ∆L aço = Lo aço - Lo al (1)
Substituindo a expressão ∆L = α Lo ∆T em 1, obtemos:
α al Lo al ∆T - α aço Lo aço ∆T = Lo aço - Lo al
2,38.10-5.50,0.∆T - 1,08.10-5.50,1.∆T = 50,1 – 50,0
119.10-5 ∆T – 54,1. 10-5∆T = 0,1
64,9.10-5 ∆T = 0,1
∆T = 154 °C
119.10-5 ∆T – 54,1. 10-5∆T = 0,1
64,9.10-5 ∆T = 0,1
∆T = 154 °C
45) Uma anel de cobre de 20 g tem um diâmetro de exatamente 1 polegada à temperatura de 0 °C. Uma esfera de alumínio tem um diâmetro de exatamente 1,002 polegada à temperatura de 100 °C. A esfera é colocada em cima do anel e permite-se que os dois encontrem seu equilíbrio térmico, sem perder calor para o ambiente. A esfera passa exatamente pelo anel na temperatura de equilíbrio. Encontre a (a) temperatura de equilíbrio e (b) a massa da esfera.



(a) Analisando a expansão térmica da esfera de alumínio e do anel de cobre. Depois da expansão, o diâmetro d da esfera de alumínio será:
O diâmetro d do anel de cobre será: 
Como na temperatura final os diâmetros da esfera e do anel serão iguais, que nos da:
Resolvendo esta equação para (T) temos:

(b) A massa da esfera e calcula por meio da troca de calor do sistema.

46) (UEL-PR) O volume de um bloco metálico sofre um aumento de 0,60% quando sua temperatura varia de

200ºC. O coeficiente de dilatação de dilatação linear médio desse metal, em ºC-1,vale:
a) 1,0.10-5 b) 3,0.10-5 c) 1,0.10-6 d) 3,0.10-4 e) 3,0.10-3
ΔV=0,006Vo --- ΔV=Vo.γ.Δt --- 0,006Vo=Vo.γ.200 --- γ=3.10-5 oC-1 --- α/1=γ/3 --- α/1=3.10-5/3 --- α=1,0.10-5 oC-1 --- Letra A
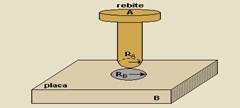
47) (UFSC-SC) Um aluno de ensino médio está projetando um experimento sobre a dilatação dos sólidos. Ele utiliza um rebite de material A e uma placa de material B, de coeficientes de dilatação térmica, respectivamente, iguais a αA e αB. A placa contém um orifício em seu centro, conforme indicado na figura. O raio RA do rebite é menor que o raio RB do orifício e ambos os corpos se encontram em equilíbrio térmico com o meio.

Assinale a(s) proposição(ões) CORRETA(S).
I. Se αA > αB a folga irá aumentar se ambos forem igualmente resfriados.
II. Se αA > αB a folga ficará inalterada se ambos forem igualmente aquecidos.
III. Se αA < αB e aquecermos apenas o rebite, a folga aumentará.
IV. Se αA = αB a folga ficará inalterada se ambos forem igualmente aquecidos.
V. Se αA = αB e aquecermos somente a placa, a folga aumentará.
VI. Se αA > αB a folga aumentará se apenas a placa for aquecida.
a) I, V e VI b) todas c) II, III e IV d) I, III e V e) II, III e IV
Resolução:
Quanto maior o coeficiente de dilatação mais o corpo se dilata quando aquecido e mais se contrais quando resfriado.
I. A se dilata mais que B --- Correta
II. Falsa --- veja (01)
III. A folga diminuirá --- Falsa
IV. Possuem diferentes Lo --- Falsa
V. Apenas a placa se dilatará --- Correta
48) (UNESP-SP) A dilatação térmica dos sólidos é um fenômeno importante em diversas aplicações de engenharia, como construções de pontes, prédios e estradas de ferro. Considere o caso dos trilhos de trem serem de aço, cujo

coeficiente de dilatação é α = 11 . 10-6 °C-1. Se a 10°C o comprimento de um trilho é de 30m, de quanto aumentaria o seu comprimento se a temperatura aumentasse para 40°C?
a) 11 . 10-4 m b) 33 . 10-4 m c) 99 . 10-4 m d) 132 . 10-4 m e) 165 . 10-4 m
a) 11 . 10-4 m b) 33 . 10-4 m c) 99 . 10-4 m d) 132 . 10-4 m e) 165 . 10-4 m
Resolução:
ΔL = Lo . α . Δθ --- ΔL = 30 . (11 . 10-6) . (40 – 10) = 99 . 10-4 m Letra C
49) (UEPG-PR)

Dilatação térmica é o fenômeno pelo qual variam as dimensões geométricas de um corpo quando este experimenta uma variação de temperatura. Sobre esse fenômeno físico, assinale o que for errado.
I. Em geral, as dimensões de um corpo aumentam quando a temperatura aumenta.
II. Um corpo oco se dilata como se fosse maciço.
III. A tensão térmica explica por que um recipiente de vidro grosso comum quebra quando é colocada água em ebulição em seu interior.
IV A dilatação térmica de um corpo é inversamente proporcional ao coeficiente de dilatação térmica do material que o constitui.
V. Dilatação aparente corresponde à dilatação observada em um líquido contido em um recipiente.
a) I, II e III b) I, III e V c) II, IV e V d) todas e) apenas a IV
Resolução:
Todas estão corretas, com exceção da IV que está errada pois, pela expressão ∆V=Vo.λ.∆θ você observa que o coeficiente de dilatação térmica (λ) é diretamente proporcional à dilatação (∆V) --- R- E.
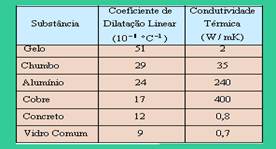
50) (UDESC-SC) A tabela abaixo apresenta uma relação de substâncias e os seus respectivos valores de coeficiente de dilatação linear e condutividade térmica, ambos medidos à temperatura de 20 °C.

Assinale a alternativa correta, tomando como base as informações acima.
a) Barras do mesmo comprimento dos metais listados na tabela sofrerão dilatações iguais, quando submetidas a uma variação de temperatura de 20 °C.
b) A condutividade térmica das substâncias permanece constante, independentemente da temperatura em que estas se encontram.
c) Substâncias que possuem maior condutividade térmica também apresentam maiores coeficientes de dilatação.
d) Dentre as substâncias listadas na tabela, o cobre é a melhor opção para fazer isolamentos térmicos.
e) Duas chapas de dimensões iguais, uma de alumínio e outra de concreto, são submetidas à mesma variação de temperatura. Constata-se então que a variação de dilatação superficial da chapa de alumínio é duas vezes maior que a da chapa de concreto.
Resolução:
Observe que o valor do coeficiente de dilatação do alumínio é o dobro do coeficiente de dilatação do concreto e, como elas tem as mesmas dimensões iniciais e sofrem a mesma variação de temperatura, a chapa de alumínio se dilata duas vezes mais do que a de concreto --- Letra E
51) Quantos cubos de gelo de 20 g, cuja temperatura inicial é - 10 °C, precisam ser colocados em 1 litro de chá quente, com temperatura inicial de 90 °C, para que a mistura final tenha uma temperatura de 10 °C? suponha que todo o gelo estará derretido na mistura final e que o calor especifico do chá seja o mesmo da água. (Dados: LF= 79,5 cal/g = 333 kJ/Kg, o calor especifico da água é 1 cal/g.°C = 4190 J/Kg.K e do gelo (-10 °C) é 0,530 cal/g.°C = 2220 J/Kg.K).



51) Quantos cubos de gelo de 20 g, cuja temperatura inicial é - 10 °C, precisam ser colocados em 1 litro de chá quente, com temperatura inicial de 90 °C, para que a mistura final tenha uma temperatura de 10 °C? suponha que todo o gelo estará derretido na mistura final e que o calor especifico do chá seja o mesmo da água. (Dados: LF= 79,5 cal/g = 333 kJ/Kg, o calor especifico da água é 1 cal/g.°C = 4190 J/Kg.K e do gelo (-10 °C) é 0,530 cal/g.°C = 2220 J/Kg.K).
Supondo que todo o gelo estará derretido na mistura final e que o calor especifico do chá seja o mesmo da água. Se considerarmos os valores para os calores específicos da água e do gelo. Sabendo que o calor especifica molar a volume constante e dado pela Eq:  , e para transição de fase temos
, e para transição de fase temos 
Sabendo que para fundir o gelo será necessário que a transição de fase seja  333000
333000
Para aquecer o gelo derretido de 0°C a 10°C temos
Calculando o calor removido da água 
Combinando todos os valores encontrados temos que o somatório do todos os Q=0

Como cada cubo de gelo tem  acrescentando
acrescentando  cubos de gelo.
cubos de gelo.
52) Dois blocos metálicos são isolados de seu ambiente. O primeiro bloco, que tem massa m1 = 3,16 kg e temperatura inicial T1 = 17 °C tem um calor específico quatro vezes maior do que o segundo bloco. Este está a uma temperatura inicial T2 = 47 °C e seu coeficiente de dilatação linear é 15 x 10-6/ °C. Quando os dois blocos são colocados juntos e alcançam seu equilíbrio térmico, a área de uma face do segundo bloco diminui em 0, 0300 %. Encontre a massa deste bloco.
O problema fala de dois blocos metálicos que são isolados de seus ambientes se pensamos nos dois blocos unidos onde sua A2f e T equivalente, desconsiderando as perdas de energia, o calor cedido pelo bloco 2(Q2) somado ao calor recebido pelo bloco 1 (Q1) deve ser nulo. 

A temperatura de equilíbrio pode ser calculada sabendo a variação da área de face do bloco 2 sabendo que a área do bloco 2 diminui 0,03% temos assim:
 Substituindo as áreas (A) por (
Substituindo as áreas (A) por (
Combinado as equações (2) em (1 ) nos da que:

Agora pratique
53) (UNIRIO) Um bloco de certo metal tem seu volume dilatado de 200cm3 para 206cm3, quanto sua temperatura aumenta de 20ºC para 520ºC. Se um fio deste mesmo metal, tendo 10cm de comprimento a 20ºC, for aquecido até a temperatura de 520ºC, então seu comprimento em centímetro passará a valer:
a) 10,1
b) 10,2
c) 10,3
d) 10,6
e) 11,2
54) (UDESC) Um recipiente para líquidos com capacidade para 120 litros, é completamente cheio a uma temperatura de 10°C. Esse recipiente é levado para um local onde a temperatura é de 30°C. Sendo o coeficiente de dilatação volumétrica do líquido igual a 1,2 x 10-3 (°C)-1, e considerando desprezível a variação de volume do recipiente, a quantidade de líquido derramado em litros é:
a) 0,024
b) 0,24
c) 2,88
d) 4,32
e) 5,76
55) (ITA) Um bulbo de vidro cujo coeficiente de dilatação linear é 3 x 10-6 °C-1 está ligado a um capilar do mesmo material. À temperatura de -10,0°C a área da secção do capilar é 3,0 x 10-4cm2 e todo o mercúrio, cujo coeficiente de dilatação volumétrico é 180 x 10-6 °C-1, ocupa o volume total do bulbo, que a esta temperatura é 0,500cm3. O comprimento da coluna de mercúrio a 90,0°C será:
a) 270mm
b) 257mm
c) 285mm
d) 300mm
e) 540mm
56) (UNIRIO) Um industrial propôs construir termômetros comuns de vidro, para medir temperaturas ambientes entre 1°C e 40°C, substituindo o mercúrio por água destilada. Cristóvão, um físico, se opôs, justificando que as leituras no termômetro não seriam confiáveis, porque:
a) a perda de calor por radiação é grande;
b) o coeficiente de dilatação da água é constante no intervalo de 0°C a 100°C;
c) o coeficiente de dilatação da água entre 0°C e 4°C é negativo;
d) o calor específico do vidro é maior que o da água;
e) há necessidade de um tubo capilar de altura aproximadamente 13 vezes maior do que o exigido pelo mercúrio.
57) (PUC-RIO 2007) Uma chapa quadrada, feita de um material encontrado no planeta Marte, tem área A = 100,0 cm² a uma temperatura de 100 ºC. A uma temperatura de 0,0 ºC, qual será a área da chapa em cm²? Considere que o coeficiente de expansão linear do material é α = 2,0 x 10−3 / ºC.
A) 74,0
B) 64,0
C) 54,0
D) 44,0
E) 34,0
Gabarito:
53) A 54) C 55) C 56) C 57) B
Fontes: www.passeiweb.com/











Tem tudo menos o que o meu professor passou
ResponderExcluirParabéns pelo desenvolvimento das soluções, ficou bem claro de entender.
ResponderExcluirmeu pirú q é claro nessa porra, seu pau no cu
Excluirassim de saúde KAKAKAKJSKJDKJKASKSA
Excluirmuito bom gostei
ResponderExcluirNao entendi a questão 17,poderia por favor me explicar?
ResponderExcluirexplica o que cada letra quer dizer nesse caralho por favor
ResponderExcluirIncrívellllllllllll! Parabéns
ResponderExcluira questão número 1, esta errada. Pois o delta L tem que ser em metros e no gráfico é passado em milimetros.
ResponderExcluirPara relaxar um pouco antes da próxima questão estou ouvindo música no http://www.ouvirradiosonline.com.br/ .
ResponderExcluirporq a resposta da 56 é letra c???
ResponderExcluirA número 3 está certa?
ResponderExcluira 3 está. a quatro não.
Excluirporque a questão 5 deu aquele resultado? não seria 1,496.10^-3?
ResponderExcluirAs questões e as resoluções estão bem explicadas mais ainda ta faltando muitas questões! As que a minha professora passou não tem nenhuma!��
ResponderExcluirnão entendi esse Vf = V + ΔV na questão 26, alguém me explica?
ResponderExcluirvolume final = volume inicial + variação volumétrica
ExcluirUma chapa quadrada , feita de um certo material , tem área A = 200,0 cm2 a uma temperatura de 10°C . A uma temperatura de 130°C , qual será a área da chapa em Cm2 ? Considere que o coeficiente de expansão linear do material é L = 2,0 × 10-3 / °C-1 .
ResponderExcluira questão 4 dá 2.10^-4 (0,0002), e não 2.10^-6 (0,000002)
ResponderExcluircheira meu rabo caralho acertei 53/57
ResponderExcluirmedicina USP só vem
Uma chapa de aço de forma quadrada tem área inicial de 10000 cm2 de lado à temperatura de 10 °C. Calcule, em cm2 , e sua variação de dilatação superficial sabendo que o coeficiente de dilatação linear desse aço é α = 12 x 10 – 6 °C – 1 e a temperatura final 110 °C. Dado: β = 2α
ResponderExcluirum determinado material de comprimento inicial 3000 m passa a apresentar um comprimento final de 3000,6 m ao sofrer um aquecimento de 5°c. cacule o coeficiente de dilatação linear desse material, ajuda nessa por favor , urgente
ResponderExcluirQueria poder ajudar, mas não sei merda nenhuma
ExcluirMtiotordes-he Zeek Ali https://www.sourcinghr.com/profile/UTorrent-181-With-DHT-Patch-Private-Patched-Serial-Key-UPDATED/profile
ResponderExcluirvalpiraro