Questões:
01. (FUVEST) Considere todas as trinta e duas seqüências, com cinco elementos cada uma, que podem ser formadas com os algarismos 0 e 1. Quantas dessas seqüências possuem pelo menos três zeros em posições consecutivas?
a) 3
b) 5
c) 8
d) 12
e) 16
02. (VUNESP) De uma urna contendo 10 bolas coloridas, sendo 4 brancas, 3 pretas, 2 vermelhas e 1 verde, retiram-se, de uma vez, 4 bolas. Quantos são os casos possíveis em que aparecem exatamente uma bola de cada cor?
a) 120
b) 72
c) 24
d) 18
e) 12
03. (MACK) Cada um dos círculos da figura ao lado deverá ser pintado com uma única cor, escolhida dentre quatro disponíveis. Sabendo-se que dois círculos consecutivos nunca serão pintados com a mesma cor, então o número de formas de se pintar os círculos é: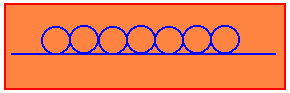
a) 100
b) 240
c) 729
d) 2916
e) 5040
04. (UEL) Um professor de Matemática comprou dois livros para premiar dois alunos de uma classe de 42 alunos. Como são dois livros diferentes, de quantos modos distintos pode ocorrer a premiação?
a) 861
b) 1722
c) 1764
d) 3444
e) 242
05. (UNIV. EST. DE FEIRA DE SANTANA) O número de equipes de trabalho que poderão ser formadas num grupo de dez indivíduos, devendo cada equipe ser constituída por um coordenador, um secretário e um digitador, é:
a) 240
b) 360
c) 480
d) 600
e) 720
06. (MACK) Os polígonos de k lados (k múltiplos de 3), que podemos obter com vértices nos 9 pontos da figura, são em número de: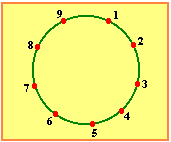
a) 83
b) 84
c) 85
d) 168
e) 169
07. (MACK) Um juiz dispõe de 10 pessoas, das quais somente 4 são advogados, para formar um único júri com 7 jurados. O número de formas de compor o júri, com pelo menos 1 advogado, é:
a) 120
b) 108
c) 160
d) 140
e) 128
08. Do cardápio de uma festa constavam dez diferentes tipos de salgadinhos dos quais só quatro seriam servidos quentes. O garçom encarregado de arrumar a travessa e servi-la foi instruído para que a mesma contivesse sempre só 2 diferentes tipos de salgadinhos frios, e só 2 diferentes dos quentes. De quantos modos diferentes, teve o garçom a liberdade de selecionar os salgadinhos para compor a travessa, respeitando as instruções?
a) 90
b) 21
c) 240
d) 38
e) 80
09. (ITA) O número de soluções inteiras, maiores ou iguais a zero, da equação x + y + z + w = 5 é:
a) 36
b) 48
c) 52
d) 54
e) 56
10. (MACK) Dentre os anagramas distintos que podemos formar com n letras, das quais duas são iguais, 120 apresentam estas duas letras iguais juntas. O valor de n é:
a) 4
b) 5
c) 6
d) 7
c) 122
a) 3
b) 5
c) 8
d) 12
e) 16
02. (VUNESP) De uma urna contendo 10 bolas coloridas, sendo 4 brancas, 3 pretas, 2 vermelhas e 1 verde, retiram-se, de uma vez, 4 bolas. Quantos são os casos possíveis em que aparecem exatamente uma bola de cada cor?
a) 120
b) 72
c) 24
d) 18
e) 12
03. (MACK) Cada um dos círculos da figura ao lado deverá ser pintado com uma única cor, escolhida dentre quatro disponíveis. Sabendo-se que dois círculos consecutivos nunca serão pintados com a mesma cor, então o número de formas de se pintar os círculos é:

a) 100
b) 240
c) 729
d) 2916
e) 5040
04. (UEL) Um professor de Matemática comprou dois livros para premiar dois alunos de uma classe de 42 alunos. Como são dois livros diferentes, de quantos modos distintos pode ocorrer a premiação?
a) 861
b) 1722
c) 1764
d) 3444
e) 242
05. (UNIV. EST. DE FEIRA DE SANTANA) O número de equipes de trabalho que poderão ser formadas num grupo de dez indivíduos, devendo cada equipe ser constituída por um coordenador, um secretário e um digitador, é:
a) 240
b) 360
c) 480
d) 600
e) 720
06. (MACK) Os polígonos de k lados (k múltiplos de 3), que podemos obter com vértices nos 9 pontos da figura, são em número de:

a) 83
b) 84
c) 85
d) 168
e) 169
07. (MACK) Um juiz dispõe de 10 pessoas, das quais somente 4 são advogados, para formar um único júri com 7 jurados. O número de formas de compor o júri, com pelo menos 1 advogado, é:
a) 120
b) 108
c) 160
d) 140
e) 128
08. Do cardápio de uma festa constavam dez diferentes tipos de salgadinhos dos quais só quatro seriam servidos quentes. O garçom encarregado de arrumar a travessa e servi-la foi instruído para que a mesma contivesse sempre só 2 diferentes tipos de salgadinhos frios, e só 2 diferentes dos quentes. De quantos modos diferentes, teve o garçom a liberdade de selecionar os salgadinhos para compor a travessa, respeitando as instruções?
a) 90
b) 21
c) 240
d) 38
e) 80
09. (ITA) O número de soluções inteiras, maiores ou iguais a zero, da equação x + y + z + w = 5 é:
a) 36
b) 48
c) 52
d) 54
e) 56
10. (MACK) Dentre os anagramas distintos que podemos formar com n letras, das quais duas são iguais, 120 apresentam estas duas letras iguais juntas. O valor de n é:
a) 4
b) 5
c) 6
d) 7
c) 122
11. De quantos modos distintos podemos colocar 3 livros juntos em uma estante de biblioteca?
12. Qual é o número possível de anagramas que se pode montar com as letras da palavra AMOR?
13. Com as 26 letras do alfabeto: A,B,C,D,...,Z e os algarismos 0,1,2,3,4,5,6,7,8,9, quantas placas de carros podem ser escritas contendo 3 letras seguidas de 4 algarismos?
14.Quantos grupos de 3 pessoas podem ser montados com 8 pessoas?
15.Existem quatro estradas ligando duas cidades A e B, e três estradas ligando as cidades B e C. De quantos modos diferentes uma pessoa pode se deslocar da cidade A até a cidade C?
16.Quantos números distintos menores que 10000 podem ser formados com algarismos diferentes da coleção: {0,1,2,3,4,5,6,7,8,9}.
GABARITO
1)C 2)C 3)D 4)B 5)E 6)E 7)A 8)A 9)E 10)C 11)6 12)24 13)78624000 14) 56 15) 12 16) 5274
QUESTÕES RESOLVIDAS
01) (FUVEST) O jogo da sena consiste no sorteio de 6 números distintos, escolhidos ao acaso, entre os números 1, 2, ..., até 50. Uma aposta consiste na escolha (pelo apostador) de 6 números distintos entre os 50 possíveis, sendo premiadas aquelas que acertarem 4 (quadra), 5 (quina) ou todos os 6 (sena) números sorteados.
Um apostador, que dispõe de muito dinheiro para jogar, escolhe 20 números e faz todos os 38.700 jogos possíveis de serem realizados com esses 20 números. Realizado o sorteio, ele verifica que todos os 6 números sorteados estão entre os 20 que ele escolheu. Além de uma aposta premiada com a sena:
a) Quantas apostas premiadas com a quina esse apostador conseguiu?
b) Quantas apostas premiadas com a quadra ele conseguiu?
A questão a) é simples: para 5 números da aposta temos a combinação dos 6 números sorteados tomados de 5 a 5 e para o último podemos escolher qualquer um dos 20 - 6 = 14 restantes. Pelo princípio multiplicativo, nossa resposta será:
Um apostador, que dispõe de muito dinheiro para jogar, escolhe 20 números e faz todos os 38.700 jogos possíveis de serem realizados com esses 20 números. Realizado o sorteio, ele verifica que todos os 6 números sorteados estão entre os 20 que ele escolheu. Além de uma aposta premiada com a sena:
a) Quantas apostas premiadas com a quina esse apostador conseguiu?
b) Quantas apostas premiadas com a quadra ele conseguiu?
A questão a) é simples: para 5 números da aposta temos a combinação dos 6 números sorteados tomados de 5 a 5 e para o último podemos escolher qualquer um dos 20 - 6 = 14 restantes. Pelo princípio multiplicativo, nossa resposta será:
A b) é parecida, mas agora temos 4 números da aposta para a combinação dos 6 números sorteados tomados de 4 a 4. Concorda que os 2 números restantes serão uma combinação dos 14 restantes tomados de 2 a 2? Portanto:
A) 8999
B) 8874
C) 7875
D) 8000
E) 7750
Há muitos casos nos quais um número é peroba. Por exemplo:
par-par-par-ímpar
par-par-ímpar-ímpar
par-ímpar-ímpar-ímpar
par-par-par-par
ímpar-ímpar-ímpar-ímpar
Então não é mais fácil descobrir quantos números não são peroba e subtrair do total de números de 4 dígitos (9000)? Vejamos quais casos são esses e calcular quantos números se enquadram neles:
par-ímpar-par-ímpar: 4 * 5 * 5 * 5 = 500 números (note que 0 não é um primeiro algarismo válido)
ímpar-par-ímpar-par: 5 * 5 * 5 * 5 = 625 números
Logo, existem 9000 - 1125 = 7875 números peroba. Alternativa c, portanto.
03)(OBM-2008)Arnaldo, Bernaldo, Cernaldo e Dernaldo baralharam as 52 cartas de um baralho e distribuíram 13 cartas para cada um. Arnaldo ficou surpreso: "Que estranho, não tenho nenhuma carta de espadas". Qual a probabilidade de Bernaldo também não ter cartas de espadas?
Precisamos calcular a probabilidade de Bernaldo não ter cartas de espadas, dentre todas as possibilidades de distribuição se Arnaldo não tem cartas de espadas. Primeiro vamos ver o que acontece se Arnaldo não tiver cartas de espada:
Para Arnaldo temos uma combinação de 39 elementos tomados de 13 a 13, para Bernaldo também (ele pode receber uma das 13 cartas de espada), para Cernaldo uma combinação de 26 elementos tomados de 13 a 13, e para Dernaldo só sobra uma possibilidade. Assim:
Agora vamos supor que Bernaldo também não tenha cartas de espadas. Assim, para Arnaldo temos uma combinação de 39 elementos tomados de 13 a 13, para Bernaldo uma combinação de 26 elementos tomados de 13 a 13, para Cernaldo uma combinação de 26 elementos tomados de 13 a 13 e para Dernaldo há apenas uma possibilidade. Pelo princípio multiplicativo:
Agora basta calcular B/A, que realizando os cálculos e simplificando nos dá a resposta:
é(são):
a) 7.
b) 0 e 7.
c) 0 e 10.
d) 1.
e) 0 e 2.
Uma questão puramente algébrica que aborda o conceito de fatorial. Lembra da definição? n! = n * (n - 1) * (n - 2) * ... * 1. Dessa definição concluímos que n! = n * (n - 1)!, concorda? Vamos tentar utilizar esse fato para simplificar a expressão acima:
Assim, concluímos que a alternativa correta é a).
05) (UFSC) Sobre uma reta são marcados 7 pontos, e sobre uma outra reta, paralela à primeira, 3 pontos. Qual é o número de triângulos com vértices em três desses pontos?
O problema equivale a descobrir quantas combinações de 10 pontos tomados de 3 a 3 podemos formar, tomando o cuidado de excluir as combinações de três pontos tomados na mesma reta. Assim, nossa resposta é:
A questão de número 13° está com gabarito errado, visto que, o problema não restringe as 3 letras ou os 4 números de não serem repetidos. Então vamos calcula-los com repetição:
ResponderExcluir26.26.26= 17576 agrupamentos de letras
Excelente material.
ResponderExcluir