Produtos notáveis são produtos de expressões algébricas que possuem uma forma geral para sua resolução. Se dividem em quadrado da soma, quadrado da diferença, produto da soma pela diferença, cubo da soma e cubo da diferença.
Quadrado da soma de dois termos
A expressão algébrica (a + b)2 apresenta uma soma de dois termos, a + b, elevada ao quadrado; é, portanto, o quadrado da soma de dois termos. Também podemos calculá-la algebricamente, multiplicando a + b por a + b:
(a + b)2 = (a + b)(a + b) =
= a . a + a . b + b . a + b . b =
= a² + ab + ba + b²
Como ab = ba, vem:
(a + b)2 = a² + 2ab + b²
Podemos explicar esse produto notável em palavras:
O quadrado da soma de dois termos é igual ao quadrado do primeiro, mais duas vezes o produto do primeiro pelo segundo, mais o quadrado do segundo termo.
Observe os exemplos:
(x + 3)² = x² + 2 . x . 3 + 3² = x² + 6x + 9
(2x + 1)² = (2x)² + 2 . 2x . 1 + 1² = 4x² + 4x + 1
(x³ + 2)² = (x³)² + 2 . x³ . 2 + 2² = x6 + 4x³ +4
Quadrado da diferença de dois termos
As expressões que possuem a forma (a – b)2 podem ser resolvidas de duas formas distintas: aplicando a propriedade distributiva da multiplicação ou a regra prática.
Utilizando a propriedade distributiva na expressão (a – b)2.
Pela definição de potenciação sabemos que (a – b)2 pode ser escrito na forma
(a – b)* (a – b).
(a – b)* (a – b) = a*a – a*b – b*a + b*b = a² – 2ab + b²
(x – 4)² = (x – 4) * (x – 4) = x*x – 4*x – 4*x + 4*4 = x² – 8x + 16
(2y – 5)² = (2y – 5) * (2y – 5) = 2y*2y – 2y*5 – 5*2y + 5*5 = 4y² – 20y + 25
(5a – 2b)² = (5a – 2b) * (5a – 2b) = 5a*5a – 5a*2b – 2b*5a + 2b*2b = 25a² – 20ab + 4b²
Utilizando a regra prática na expressão (a – b)2.
“O quadrado do primeiro termo menos, duas vezes o primeiro termo vezes o segundo termo, mais o quadrado do segundo termo.”
(y – 6)² = (y)² – 2*y*6 + (6)² = y² – 12y + 36
(4b – 9)² = (4b)² – 2*4b*9 + (9)² = 16b² – 72b + 81
(7y – 6x)² = (7y)² – 2*7y*6x + (6x)² = 49y² – 84xy + 36x²
(10x – 2z)² = (10x)² – 2*10x*2z + (2z)² = 100x² – 40xz + 4z
Produto da soma pela diferença
Uma situação interessante envolvendo expressões algébricas se apresenta na seguinte forma:
(a + b)(a – b), sendo denominada Produto da Soma pela Diferença, podendo ser resolvida através da propriedade distributiva da multiplicação ou através de uma regra prática. Essa expressão pode ser considerada um produto notável, pela característica regular apresentada na resolução de situações semelhantes.
Aplicando a propriedade distributiva na resolução da expressão (a + b)(a – b).
(a + b)(a – b) = a*a – a*b + b*a – b*b = a² – b² Note que os termos – ab e + ba são opostos, por isso se anulam.
(2x + 4)(2x – 4) = 2x*2x – 2x*4 + 4*2x – 4*4 = 4x² – 8x + 8x – 16 = 4x² – 16
(7x + 6)(7x – 6) = 7x*7x – 7x*6 + 6*7x – 6*6 = 49x² – 42x + 42x – 36 = 49x² – 36
(10x³ – 12)(10x³ + 12) = 10x³*10x³ + 10x³*12 – 12*10x³ –12*12 = 100x6 + 120x³ – 120x³ – 144 = 100x6 – 144
(20z + 10x)(20z – 10x) = 20z*20z – 20z*10x + 10x*20z – 10x*10x = 400z² – 200zx + 200xz – 100x² = 400z² – 100x²
Aplicando a regra prática
A aplicação da regra prática se dá através da seguinte situação: “o primeiro termo elevado ao quadrado menos o segundo termo elevado ao quadrado”
(4x + 7)(4x – 7) = (4x)² – (7)² = 16x² – 49
(12x + 8)(12x – 8) = (12x)² – (8)² = 144x² – 64
(11x² – 5x)(11x² + 5x) = (11x²)² – (5x)² = 121x4 – 25x²
(20b – 30)(20b + 30) = (20b)² – (30)² = 400b² – 900
Cubo da soma
Sejam a e b números reais diferentes de zero. Temos que:
(a + b)3 = (a + b)2(a + b) = (a2 + 2ab + b2)(a + b) = a3 + 2a2b +ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3.
Observe que utilizamos o quadrado da soma, que é outro produto notável, para obter o cubo da soma. De uma forma geral, o cubo da soma pode ser obtido da seguinte maneira:
(a + b)3 = (a + b)2(a + b) = (a2 + 2ab + b2)(a + b) = a3 + 2a2b +ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3.
Observe que utilizamos o quadrado da soma, que é outro produto notável, para obter o cubo da soma. De uma forma geral, o cubo da soma pode ser obtido da seguinte maneira:
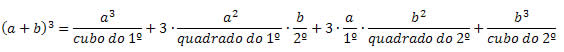
Cubo da diferença
O cubo da diferença é feito de maneira análoga ao cubo da soma. Observe:
(a – b)3 = (a – b)2(a – b) = (a2 – 2ab + b2)(a – b) = a3 – 3a2b + 3ab2 – b3
De uma forma geral, temos:
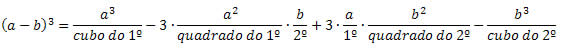
Vejamos alguns exemplos para melhor esclarecimento.
Exemplo 1. Desenvolva os seguintes produtos notáveis.
Solução:
Exemplo 1. Desenvolva os seguintes produtos notáveis.
Solução:
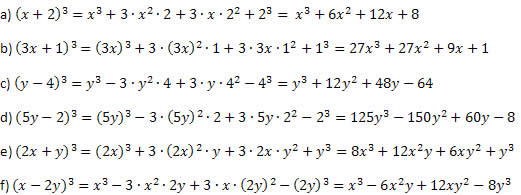
Procedendo como foi explicado antes do exemplo e tendo o cuidado ao realizar as potências e a multiplicações, não há como errar. O procedimento é sempre o mesmo para o cubo da soma e para o cubo da diferença, diferindo somente o sinal do segundo membro e do último.
Exemplo 2. Simplifique a expressão abaixo.
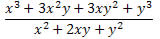
Solução: Observe que no numerador e no denominador da fração aparecem dois produtos notáveis. No numerador há um cubo da soma de dois termos que foi desenvolvido e no denominador, um quadrado da soma de dois termos. Assim, podemos reescrevê-los da seguinte forma:
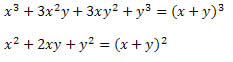
Logo, a expressão pode ser escrita como:
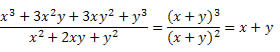
Para chegar ao resultado utilizamos a propriedade da divisão de potências de bases iguais (conserva a base e subtrai os expoentes).
Exemplo 3. Desenvolva o seguinte produto notável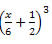
Exemplo 3. Desenvolva o seguinte produto notável
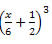
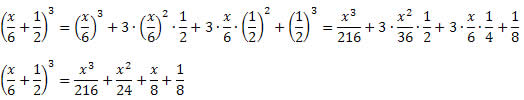
Quadrado da Soma de Três Termos
O quadrado da soma de três termos é igual ao quadrado do primeiro termo, mais o quadrado do segundo termo, mais o quadrado do terceiro termo, mais duas vezes o produto do primeiro pelo segundo termo, mais o duas vezes o produto do primeiro pelo terceiro termo, mais o duas vezes o produto do segundo pelo terceiro termo:
Exemplos:



RESUMO
Produtos notáveis
|
Exemplos
|
(a+b)2 = a2+2ab+b2
|
(x+3)2 = x2+6x+9
|
(a-b)2 = a2-2ab+b2
|
(x-3)2 = x2-6x+9
|
(a+b)(a-b) = a2-b2
|
(x+3)(x-3) = x2-9
|
(x+a)(x+b) = x2+(a+b)x+ab
|
(x+2)(x+3) = x2+5x+6
|
(a+b)3 = a3+3a2b+3ab2+b3
|
(x+2)3 = x3+6x2+12x+8
|
(a-b)3 = a3-3a2b+3ab2-b3
|
(x-2)3 = x3-6x2+12x-8
|
(a+b)(a2-ab+b2) = a3+b3
|
(x+2)(x2-2x+4) = x3+8
|
(a-b)(a2+ab+b2) = a3-b3
|
(x-2)(x2+2x+4) = x3-8
|
Fonte: www.coladaweb.com.br
www.matematicadidatica.com.br
www.matematicadidatica.com.br
Exercícios sobre produtos notáveis
1) Simplifique as expressões:
2) Desenvolva:
a) (x+y)2–x2-y2
(x+y)2–x2-y2 = x2+2xy+y2–x2-y2 = 2xy
b) (x+2)(x-7)+(x-5)(x+3)
(x+2)(x-7)+(x-5)(x+3) = x2+(2+(-7))x+2.(-7) + x2+(-5+3)x+3.(-5) =
x2-5x-14+ x2-2x-15 = 2x2-7x-29
c) (2x-y)2-4x(x-y)
(2x-y)2-4x(x-y) = (2x)2-2.2x.y+y2-4x2+4xy = 4x2-4xy+y2-4x2+4xy = y2
2) Desenvolva:
a) (3x+y)2
(3x+y)2 = (3x)2+2.3x.y+y2 = 9x2+6xy+y2
b) ((1/2)+x2)2
((1/2)+x2)2 = (1/2)2+2.(1/2).x2+(x2)2 = (1/4) +x2+x4
c) ((2x/3)+4y3)2
((2x/3)+4y3)2 = (2x/3)2-2.(2x/3).4y3+(4y3)2= (4/9)x2-(16/3)xy3+16y6
d) (2x+3y)3
(2x+3y)3 = (2x)3+3.(2x)2.3y+3.2x.(3y)2+(3y)3 = 8x3+36x2y+54xy2+27y3
e) (x4+(1/x2))3
(x4+(1/x2))3 = (x4)3+3.(x4)2.(1/x2)+3.x4.(1/x2)2+(1/x2)3 = x12+3x6+3+(1/x6)
f) ((2x/3)+(4y/5)).((2x/3)-(4y/5)
(2x/3)+(4y/5)).((2x/3)-(4y/5)) = (2x/3)2-(4y/5)2 = (4/9)x2-(16/25)y2
3) Se x - y = 7 e xy = 60, então o valor da expressão x² + y² é:
a) 53
b) 109
c) 169
d) 420
Solução:
Do problema, temos a seguinte equação x - y = 7, a princípio não está muito claro o valor de x² + y², mas vamos traçar uma estratégia para resolução da questão:
Na equação x - y = 7, vamos elevar os dois membros ao quadrado, ficando assim:
(x - y)² = 7², desenvolvendo temos:
x² - 2xy + y² = 49, veja que já apareceram o x² e y², arrumando
x² + y² = 49 + 2xy, mas xy = 60 e daí
x² + y² = 49 + 2.60, resolvendo:
x² + y² = 49 + 120, logo x² + y² = 169.
Utilizamos a estratégia de elevar os dois membros da equação ao quadrado - podemos fazer isto, desde que façamos em ambos os membros - e logo apareceu x² + y².
4) A expressão (x - y)² - (x + y)² é equivalente a:
a) 0
b) 2y²
c) -2y³
d) -4xy
Solução:
Primeiro vamos desenvolver os binômios separadamente:
(x - y)² - (x + y)²
(x-y)² = x² - 2xy + y² e (x + y)² = x² + 2xy + y²
Após desenvolver, voltamos para a expressão e substituímos:
(x - y)² - (x + y)² = x² - 2xy + y² - (x² + 2xy + y²) = x² - 2xy + y² - x² - 2xy - y² =
x² - x² - 2xy - 2xy + y² - y² = -2xy - 2xy = - 4xy
Logo, (x - y)² - (x + y)² = - 4xy
5) (TRT-2011) Indagado sobre o número de processos que havia arquivado certo dia, um Técnico Judiciário, que gostava muito de Matemática, respondeu:
- O número de processos que arquivei é igual a (12,25)^2-(10,25)^2
Chamando X o total de processos que ele arquivou, então é correto afirmar que:
a)38 < X < 42.
b) X > 42.
c) X < 20.
d)20 < X < 30.
e)30 < X < 38
Solução:
Quer dizer então que quando tenho o produto da soma pela diferença posso reescrever isto de outra forma que talvez me ajude a resolver os problemas dessa natureza? Exatamente.
Acompanhe alguns exemplos:
Entendeu? Espero que sim.
Agora vamos voltar ao problema proposto, temos que:
O número de processos que arquivei é igual a (12,25)^2-(10,25)^2.
Pessoal, observando os exemplos acima, como podemos reescrever este produto((12,25)^2-(10,25)^2)?
Atenção!!!
6) Calcule o produto da soma pela diferença de dois termos:
b) (y – 7 ) . (y + 7) =
c) (x + 3) . (x – 3) =
d) (2x + 5 ) . (2x – 5) =
e) (3x – 2 ) . ( 3x + 2) =
f) (5x + 4 ) . (5x – 4) =
g) (3x + y ) (3x – y) =
h) ( 1 – 5x) . (1 + 5x) =
i) (2x + 3y) . (2x – 3y) =
j) (7 – 6x) . ( 7 + 6x) =
l) (1 + 7x²) . ( 1 – 7x²) =
7) Desenvolva:
a) ( x + y)³ =
b) (x – y)³ =
c) (m + 3)³ =
d) (a – 1 )³ =
e) ( 5 – x)³ =
8) Calcule o valor numérico de
110M , sabendo que M+2=a2b2+b2a2+2−−−−−−−−−−−√ , a=0,998 e b=1 .
b) (x – y)³ =
c) (m + 3)³ =
d) (a – 1 )³ =
e) ( 5 – x)³ =
8) Calcule o valor numérico de
a) 249.500
b)24950
c)2495
d)249,5
e)24,49
b)
c)
d)
e)
9) A expressão (a + b + c)² é igual a
b) a² + b² + c² + 2ab + 2ac + 2bc
c) a² + b² + c² + 2abc
d) a² + b² + c² + 4abc
e) a² + 2ab + b² + 2bc + c²
10) (FEI 95)Simplificando a expressão, (imagem abaixo) obtemos:
b) a² + b²
c) ab
d) a² + ab + b²
e) b - a

11) Seja N o resultado da operação 375²-374². A soma dos algarismos de N é:
a) 18
b) 19
c) 20
d) 21
e) 22
b) 19
c) 20
d) 21
e) 22
12) Efetuando-se (579865)² - (579863)², obtém-se
a) 4
b) 2 319 456
c) 2 319 448
d) 2 086 246
e) 1 159 728
b) 2 319 456
c) 2 319 448
d) 2 086 246
e) 1 159 728
13) O produto (x + 1)(x² - x +1) é igual a:
a) x³-1
b) x³ + 3x² - 3x + 1
c) x³ + 1
d) x³ - 3x² + 3x - 1
e) x² + 2
Gabarito:
10) D
11) C
12) B
13) C
b) x³ + 3x² - 3x + 1
c) x³ + 1
d) x³ - 3x² + 3x - 1
e) x² + 2
Gabarito:
6) a) (R : x² - y²) b) ( R : y² - 49) c) ( R: x² - 9) d) ( R: 4x² - 25) e) ( R: 9x² - 4 ) f) ( R: 25x² - 16)
g) (R: 9x² - y² ) h) ( R: 1 - 25x² ) i) ( R: 4x² - 9y² ) j) (R: 49 - 36x²) l) (R: 1 - 49x⁴)
7) a) (R: x³ + 3x²y + 3xy² + y³) b) (R: x³ - 3x²y + 3xy² - y³) c) ( R: m³ + 9m² + 27m +27)
d) (R: a³ - 3a² + 3a -1) e) (R: 125 - 75x + 15x² -x³)
8) B
9) B10) D
11) C
12) B
13) C


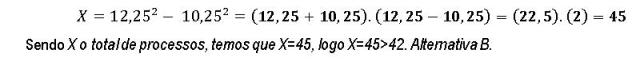
Olá. Por favor poste o desenvolvimento das contas 8 e 10, não consigo desenvolver...
ResponderExcluirTambém não. o que que é aquele numero ou sei la em cima do A e do B?
ExcluirEste comentário foi removido pelo autor.
Excluir11 não é letra A)? Por mim é.
Excluir10:(a²+b+ab²)*(1/a³-1/b³)/(1/a²-1/b²)
ExcluirPrimeiramente fazemos a distribuição de acordo com os produtos notáveis,que fica:a²+ab²+ab4++ab²+b²+ab3+ab4+ab3+ab4
Ao cortamos os semelhantes ficamos com:
a²+b²
Assim nossa conta fica:
a²+b²*(1/a³-1/b³)/(1/a²-1/b²)
Ao resolvermos ficamos com:
a²+b²* 1/ab(elevado a 3)/ 1/ab(elevado a 2)
a²+b²*1/ab(aqui os expoentes somem pois subtraímos ambos 3-2)
a²+ab+b²
questão 11
Excluir375 elevado a 2: 140625
374 elevado a 2: 139876
ao subtrairmos 140625-139876= 749
O exercício quer que somamos os algarismos do resultado,então ficamos com: 7+4+9=20
Oi. Seu site está muito bom de conteúdo, mais tem algumas coisas que estão erradas.
ResponderExcluirPorque no quarto exemplo do quadrado da diferença de dois termos no final não dá 4z² ?
ResponderExcluirMuito bom!
ResponderExcluirMuito bom!
ResponderExcluirÓtimo conteúdo!
ResponderExcluirParabéns ,ótimo site e ótimas explicações também .
ResponderExcluirola não entendi a 12 me explica pff
ResponderExcluirVocê irá fazer 579865 multiplicado por ele mesmo,pois este está elevado ao quadrado.
ResponderExcluirdepois você irá fazer o mesmo com o 579863.
Em seguida você irá subtrair os resultados dessas duas multiplicações. O resultado será aproximado ao da alternativa B, que é a correta.