Artigo sobre o estudo da elipse: conceito, elementos, equação reduzida e coordenadas polares com questões resolvidas.
Elipse
Conceito de Elipse
Elipse é a cônica definida na interseção de um plano que atravessa a superfície de um cone;
Elementos da Elipse:

F1 e F2 → são os focos
C → Centro da elipse
2c → distância focal
2a → medida do eixo maior
2b → medida do eixo menor
c/a → excentricidade
Há uma relação entre os valores a, b e c→ a2 = b2+c2
Equação reduzida da elipse
Seja P(x, y) um ponto qualquer de uma elipse e sejam F1(c,0) e F2(-c,0) os seus focos. Sendo 2a o valor constante com c < a, como vimos acima, podemos escrever:
PF1 + PF2 = 2.a

onde o eixo A1A2 de medida 2a, é denominado eixo maior da elipse e o eixo B1B2 de medida 2b, é denominado eixo menor da elipse.
PF1 + PF2 = 2.a

onde o eixo A1A2 de medida 2a, é denominado eixo maior da elipse e o eixo B1B2 de medida 2b, é denominado eixo menor da elipse.
Usando a fórmula da distancia entre dois pontos, poderemos escrever:

Observe que x – (-c) = x + c.
Quadrando a expressão acima, vem:

Com bastante paciência , desenvolvendo a expressão acima e fazendo a2 – c2 = b2, a expressão acima depois de desenvolvida e simplificada, chegará a:b2.x2 + a2.y2 = a2.b2
Dividindo agora, ambos os membros por a2b2 vem finalmente:
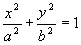
que é a equação da elipse de eixo maior horizontal e centro na origem (0,0).
Observe que x – (-c) = x + c.
Quadrando a expressão acima, vem:
Com bastante paciência , desenvolvendo a expressão acima e fazendo a2 – c2 = b2, a expressão acima depois de desenvolvida e simplificada, chegará a:b2.x2 + a2.y2 = a2.b2
Dividindo agora, ambos os membros por a2b2 vem finalmente:
que é a equação da elipse de eixo maior horizontal e centro na origem (0,0).
Notas:
1) como a2 – c2 = b2 , é válido que: a2 - b2 = c2, onde c é a abcissa de um dos focos da elipse.
2) como a excentricidade e da elipse é dada por e = c/a , no caso extremo de termos b = a, a curva não será uma elipse e sim, uma circunferência, de excentricidade nula, uma vez que sendo b = a resulta c = 0 e, portanto e = c/a = 0/a = 0.
3) o ponto (0,0) é o centro da elipse.
4) se o eixo maior da elipse estiver no eixo dos y e o eixo menor estiver no eixo dos x, a equação da elipse de centro na origem (0,0) passa a ser:
Fontes: http://www.algosobre.com.br/
http://www.brasilescola.com/
http://www.profcardy.com/
http://pt.wikipedia.org/wiki/Wikip%C3%A9dia:P%C3%A1gina_principal
http://estagio2001.no.sapo.pt/
Questões resolvidas sobre elipse
1) (CESCEA) Determine as coordenadas dos focos da elipse de equação
9x2 + 25y2 = 225.
Solução:
Dividindo ambos os membros por 225, vem:
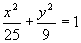
Daí, vem que: a2=25 e b2=9, de onde deduzimos: a = 5 e b = 3.
Portanto, como a2 = b2 + c2, vem que c = 4.
Portanto, as coordenadas dos focos são: F1(4,0) e F2(-4,0).
Daí, vem que: a2=25 e b2=9, de onde deduzimos: a = 5 e b = 3.
Portanto, como a2 = b2 + c2, vem que c = 4.
Portanto, as coordenadas dos focos são: F1(4,0) e F2(-4,0).
2) Determine a excentricidade da elipse de equação 16x2 + 25y2 – 400 = 0.
Solução:
Temos: 16x2 + 25y2 = 400. Observe que a equação da elipse não está na forma reduzida. Vamos dividir ambos os membro por 400. Fica então:
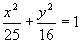
Portanto, a2 = 25 e b2 = 16. Daí, vem: a = 5 e b = 4.
Como a2 = b2 + c2 , vem substituindo e efetuando, que c = 3
Portanto a excentricidade e será igual a : e = c/a = 3/5 = 0,60
Resposta: 3/5 ou 0,60.
Como a2 = b2 + c2 , vem substituindo e efetuando, que c = 3
Portanto a excentricidade e será igual a : e = c/a = 3/5 = 0,60
Resposta: 3/5 ou 0,60.
3) A equação de uma elipse é x²/p² + y²/q² = 1. Sabendo que a elipse passa pelos pontos (2;1) e (raiz de 2;2), determine p e q.
Solução:
4/p²+1/q²=1
4q²+p²=p².q².......equação(1)
Substituindo x por √2 e y por 2, temos:
2/p²+4/q²=1
2q²+4p²=p².q².......equação(2)
Resolvendo o sistema de equações equação(1) e equação(2):
4q²+p²=p².q²
2q²+4p²=p².q²
temos:
equação(1) - 2 . equação(2):
4q²+p² = p².q²
-4q²-8p²=-2p².q²
------------------------
/ -7p²=-p².q²
q²=7....q = √7
4.7+p² = 7.p²
6.p²=28....p = √(14/3)
Logo a equação da elipse é:
3x²/14+y²/7=1
Resposta: p=√(14/3) e q=√7
4) Determine a equação reduzida da elipse sabendo que um dos focos é F1(0 , -3) e que o eixo menor mede 8.
Solução:
Temos que:
Se F1(0 , -3) → c = 3 e o foco está sobre o eixo y.
2b = 8 → b = 4
Usando a relação notável: a2 = b2+c2, obtemos:
a2 = 42+32 → a2 = 16 + 9 → a2 = 25 → a = 5
Se F1(0 , -3) → c = 3 e o foco está sobre o eixo y.
2b = 8 → b = 4
Usando a relação notável: a2 = b2+c2, obtemos:
a2 = 42+32 → a2 = 16 + 9 → a2 = 25 → a = 5
Assim, a equação reduzida da elipse será:
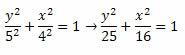
5) Encontre a equação da elipse que tem como eixo maior a distância entre as raízes da parábola de equação y = x² - 25 e excentricidade e = 3/5.
Solução:
Resolvendo a equação:
x² - 25 = 0
x² = 25
x = ± 5
Sabendo que a distância entre as raízes da equação é o eixo maior da elipse, podemos concluir que esse eixo esta localizado no eixo x e que seu valor é 10. Assim:
d = 2a = 10
a = 5
Admitindo que e = 3/5, podemos dizer que c = 3
Com os valores de c e a, conseguimos encontrar b. Já que:
a² = b² + c²
25 = b² + 9
b = 4
Então, a equação da elipse é:
x²/25 + y²/16 = 1
6) Sabendo que o centro (0,0), o comprimento do eixo menor é 6 e a distância focal é 10, determine a equação geral e reduzida da elipse.
Solução:
Na equação da Elipse o "a" fica no denominador do eixo maior que é também onde sempre estão os focos que nesta questão está no eixo "x".
(X - Xo)² . .(Y - Yo)²
----------- + ------------ = 1
. . a² . . . . . . b²
centro (Xo, Yo) = (0, 0)
O eixo menor é 2b = 6 ............. b = 3
A distância focal é 2c = 10 ....... c = 5
É lei na elipse a² = b² + c²
(X - Xo)² . .(Y - Yo)²
----------- + ------------ = 1
. . a² . . . . . . b²
centro (Xo, Yo) = (0, 0)
O eixo menor é 2b = 6 ............. b = 3
A distância focal é 2c = 10 ....... c = 5
É lei na elipse a² = b² + c²
a² = 3² + 5²
a² = 9 + 25
a² = 34 ........... a = √34
A equação reduzida fica:
X² . . .Y²
---- + ----- = 1
34 . . . 9
a² = 9 + 25
a² = 34 ........... a = √34
A equação reduzida fica:
X² . . .Y²
---- + ----- = 1
34 . . . 9
7) Mostre que o conjunto de pontos definidos pelo sistema seguinte é uma elipse e determine as coordenadas do centro, dos focos e dos vértice.

Temos:

Então,
O eixo maior é vertical, logo
Os focos são os pontos:
Os vértices são os pontos:
8) Considere a equação
Solução:
Para obtermos a equação reduzida, teremos de transformar a equação que define a elipse do problema numa equação equivalente.
Vem sucessivamente:

Vem sucessivamente:

que nos mostra que o centro da elipse é o ponto  .
.
Como  e
e  , vem
, vem  e portanto
e portanto  , pois
, pois  .
.
Para uma elipse geometricamente igual à dada mas com centro em (0,0), os focos seriam os pontos  e
e  . Então, para obter os focos da elipse do problema é necessário adicionar o vector (-1,3), donde
. Então, para obter os focos da elipse do problema é necessário adicionar o vector (-1,3), donde
Focos:
Para os vértices faz-se o mesmo raciocínio, logo
Vértices: 
Excentricidade:  .
.
9) A órbita da Terra à volta do Sol é uma elipse quase circular. O Sol é um dos focos dessa elipse e o eixo maior e o eixo menor medem 299 329 800 e 299 288 058 Km, respectivamente. Qual é a distância mínima e a distância máxima da Terra ao Sol?
Solução:
Consideremos  .
.
Então temos:
Então temos:
Sendo  , vem
, vem  . Então c=2499375,3
. Então c=2499375,3
Logo a distância máxima é dada por  e a distância mínima é dada por
e a distância mínima é dada por 

10) Dada a Elipse de equação  , escreve uma equação da recta tangente à elipse no ponto
, escreve uma equação da recta tangente à elipse no ponto  .
.
Solução:

Como se pretende a equação da recta tangente no ponto
 ,
,  .
.Portanto a equação da recta pretendida é:

11) (EXTRA) Dada a equação de uma Elipse a seguir 25x² + 16y² + 288y + 896 = 0
As medidas dos seus eixos Maior e Menor são, respectivamente:
a) 25 e 16
b) 896 e 288
c) 10 e 8
d) 20 e 16
e) n.d.r.a
12) (EXTRA) Dada a equação de uma Elipse a seguir 25x² + 16y² + 288y + 896 = 0
As coordenadas dos seus focos são:
a) (16, 25) e (-16, -25)
b) (0, 3) e (0, -3)
c) (3, 0) e (-3, 0)
d) (0, -6) e (0, -12)
e) n.d.r.a
13) (UFRJ) Dada a equação de Elipse a seguir

a) (16, 25) e (-16, -25)
b) (0, 3) e (0, -3)
c) (3, 0) e (-3, 0)
d) (0, -6) e (0, -12)
e) n.d.r.a
14) Dada a equação a seguir

O centro da Elipse determinada pelos pontos (x, y) descritas pela equação é:
a) (3, 9)
b) (2, 4)
c) (25, 9)
d) (-9, 2)
e) (2, -9)
15) Dada a equação de Elipse a seguir
 A medida do seu Eixo Maior é:
A medida do seu Eixo Maior é:
a) 25
b) 16
c) 10
d) 8
e) 4

a) 25
b) 16
c) 10
d) 8
e) 4
16) Com base no gráfico de uma elipse a seguir:

Uma equação que descreve os pontos (x, y) de seu gráfico pode ser:
(A) 9x2 + 25y2 = 125
(B) 9x2 + 25y2 = 25
(C) 16x2 + y2 = 1
(D) 25x2 + 9y2 = 225
(E) 9x2 + 25y2 = 225

Uma equação que descreve os pontos (x, y) de seu gráfico pode ser:
(A) 9x2 + 25y2 = 125
(B) 9x2 + 25y2 = 25
(C) 16x2 + y2 = 1
(D) 25x2 + 9y2 = 225
(E) 9x2 + 25y2 = 225
17) Uma elipse com centro na origem tem medida do eixo maior 18 e distância focal 6. Determine uma possível equação desta elipse.
Gabarito:
11) C 12) D 13) D 14) E 15) C 16) E 17) A 18) B 19) E 20) x2 + 2y2 = 3.
(A) 728x2 + 9y2 = 58.968
(B) x2 + 9y2 = 58.968
(C) 728x2 + 81y2 = 58.968
(D) 728x2 – 9y2 = 58.968
(E) x2 + y2 = 58.968
18) Dada uma equação da elipse:
9x² + 4y² = 36
O quadrado da distância focal é:
a) 80
b) 77
c) 70
d) 13
e) 2
19) (UEL) Em uma praça dispõe-se de uma região retangular de 20 m de comprimento por 16 m de largura para construir um jardim. A exemplo de outros canteiros, este deverá ter a
forma elíptica e estar inscrito nessa região retangular. Para aguá-lo, serão colocados dois aspersores nos pontos que correspondem aos focos da elipse. Qual será a distância
entre os aspersores?
a) 4 m b) 6 m c) 8 m d) 10 m e) 12 m
20) Determinar a equação da elipse com centro na origem, que passa pelo ponto P(1,1) e tem um foco F(-Ö6 /2, 0).
9x² + 4y² = 36
O quadrado da distância focal é:
a) 80
b) 77
c) 70
d) 13
e) 2
19) (UEL) Em uma praça dispõe-se de uma região retangular de 20 m de comprimento por 16 m de largura para construir um jardim. A exemplo de outros canteiros, este deverá ter a
forma elíptica e estar inscrito nessa região retangular. Para aguá-lo, serão colocados dois aspersores nos pontos que correspondem aos focos da elipse. Qual será a distância
entre os aspersores?
a) 4 m b) 6 m c) 8 m d) 10 m e) 12 m
20) Determinar a equação da elipse com centro na origem, que passa pelo ponto P(1,1) e tem um foco F(-Ö6 /2, 0).
Gabarito:
11) C 12) D 13) D 14) E 15) C 16) E 17) A 18) B 19) E 20) x2 + 2y2 = 3.






 , sendo e a excentricidade.
, sendo e a excentricidade. é chamado de anomalia verdadeira e é representado pela letra grega
é chamado de anomalia verdadeira e é representado pela letra grega 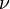 (nu ou ni)
(nu ou ni)
Gabarito 12 está errado
ResponderExcluirGabarito tudo errado, que isso..
ResponderExcluirO gabarito 12 está correto. Observe que o centro é C(0,-9), daí os focos F1 e F2 estarão |3| acima e abaixo no eixo y. Logo os focos são F1(0, -6) e F2(0, -12).
ResponderExcluirRapaz... Aprende o básico, os focos tem coordenadas padrão F1(-c,0) e F2(c,0),e se ele dizer que os focos estão sobre o eixo y -que não é o caso - as coordenadas serão F1(0,c) e F2(0,-c), a questão nem precisa de cálculo é só saber o básico, a única que pode ser é a letra C)
ExcluirNa questão 3, das solucionadas. Pq o "q" do sistema irá ficar raiz de 7? a equação estava assim "7p^2= -p^2 x q ^2", não consigo compreender.
ResponderExcluirEste comentário foi removido pelo autor.
ResponderExcluirQuestão 4 está errada. Já que o eixo maior está no eixo y o que muda são os denominadores e não os numeradores.
ResponderExcluiro gabarito tá certo, é só fazer os calculos com calma que dá certo.
ResponderExcluirO gabarito da 13 com toda certeza tá errado, pois as coordenadas dos focos, isto é, c têm um padrão: F1 (-c,0) F2(c,0). No caso dessa questão nem precisa fazer cálculo a resposta certa é a letra C)
ResponderExcluirMesma coisa da 12.
ExcluirO gabarito tá certo, pq essa elipse não tem centro na origem então esse c vai ser dependente do valor do centro!
ResponderExcluir