QUESTÕES DE CONCURSOS, VESTIBULARES E NOTÍCIAS DE CONCURSOS EM ABERTO: Velocidade Escalar Média e deslocamento escalar: exemplos e questões resolvidas

quarta-feira, 31 de julho de 2013

Velocidade Escalar Média e deslocamento escalar: exemplos e questões resolvidas

Artigo sobre velocidade escalar média, trajetória, intervalo de tempo e deslocamento com questões resolvidas.

Velocidade escalar média

A velocidade escalar média é a relação entre o deslocamento escalar ∆s e o correspondente intervalo de tempo ∆t

Onde:

ΔS é a variação da posição do móvel: ΔS = S_f - S_i
Δt é a variação do tempo: Δt = t_f - t_i

No Sistema Internacional (SI), a unidade de velocidade é metro por segundo (m/s). É também muito comum o emprego da unidade quilômetro por hora (km/h). Pode-se demonstrar que 1 m/s é equivalente a 3,6 km/h.

Assim temos:

Como exemplo, suponha um carro efetuando um deslocamento escalar de 36 km num intervalo de tempo de 0,50 h. A sua velocidade escalar média neste percurso corresponde a:

O resultado encontrado (72 km/h = 20 m/s), significa a suposta velocidade escalar constante que o carro poderia ter utilizado no trajeto.

Velocidade escalar instantânea

A velocidade escalar instantânea é a velocidade em determinado instante específico. Para calcular a velocidade instantânea é necessária a utilização de uma operação matemática denominada de limite. Nessa operação matemática pegamos intervalos de tempo muito pequenos, ou seja, fazemo-los tender para zero. Matematicamente temos a seguinte relação que define a velocidade escalar instantânea:

Na equação acima, lim significa limite.
Em termos práticos, podemos determinar a velocidade escalar instantânea da seguinte forma:

O físico e matemático inglês Isaac Newton descobriu, no século XVII, o processo matemático denominado derivação de funções, que permitiu obter certas grandezas instantâneas. A partir disto, temos:

Simbolicamente, isto é expresso assim:

(lê-se derivada de s em relação a t)

Cada função matemática tem a sua derivada específica. Para o estudo da Cinemática, no ensino médio, tem grande importância a derivada de uma função polinomial, a qual é calculada de acordo com a técnica descrita a seguir.

• Função horária dada:

• Indicação da derivada:

• Cálculo da derivada:

A expressão final é denominada função horária da velocidade. Ela nos permite determinar a velocidade escalar num instante t qualquer.

Exemplo:

A função horária do espaço de um móvel é dada por:
s = 2t³ + 4t² - 5t + 7 (SI)
Obter a velocidade escalar do móvel num instante t.

Resolução:

Trajetória, Intervalo de Tempo e Deslocamento Escalar - definição e exemplos

Trajetória

É um percurso, uma estrada, por exemplo. Toda trajetória tem um sentido, esse sentido irá indicar se o movimento é progressivo ou retrógrado. Se o corpo estiver se movimentando para a mesma direção adotada pela trajetória, temos um movimento progressivo, mas se estiver no sentido oposto, temos um movimento retrógrado.

Ex.:

Na trajetória acima o sentido é da esquerda pra direita, então o carrinho está em um movimento retrógrado, pois ele está indo no sentido oposta ao da trajetória.

Intervalo de Tempo

É a subtração do Tempo final pelo Tempo inicial.

Deslocamento Escalar

A posição de um objeto (móvel) pode variar à medida que ele se afasta ou se aproxima do referencial, e a essa variação de posição chamamos deslocamento.

O deslocamento de um móvel (objeto) é representado por ΔS (lê- se: "delta s") e corresponde à localização que o móvel ocupa no final do movimento (posição final s) menos sua posição no início do movimento (posição inicial S0).

A fórmula é dada por:

ΔS = S – S₀

Exemplo:
Um automóvel, sobre uma estrada, parte da cidade A (km 10) no instante 3 horas, passa pela cidade B (km 410) no instante 7 horas e chega à cidade C (km 310) às 8 horas.

Podemos então determinar:

I. Entre as cidades A e B

O espaço inicial (S₀): S₀ = 10 km

O espaço final (S): S = 410 km

O instante inicial (t₀): t₀ = 3 h

O instante final (t): t = 7 h

O intervalo de tempo (Dt): Dt = t - t₀

Dt_AB = 7 - 3 = 4

Dt_AB = 4h

Deslocamento (DS): DS = S - S₀

DS_AB = 410 - 10 = 400

DS_AB = 400km

II. Entre as cidades B e C

O espaço inicial (S₀): S₀ = 410 km

O espaço final (S): S = 310 km

O instante inicial (t₀): t₀ = 7h

O instante final (t): t = 8 h

O intervalo de tempo (Dt): Dt = t - t₀

Dt_BC = 8 - 7 = 4

Dt_BC = 1h

Deslocamento (DS): DS = S - S₀

DS_BC = 310 - 410 = -100

DS_BC = -100km

III. Entre as cidades A e C

O espaço inicial (S₀): S₀ = 10 km

O espaço final (S): S = 310 km

O instante inicial (t₀): t₀ = 3 h

O instante final (t): t = 8 h

O intervalo de tempo (Dt): Dt = t - t₀

Dt_AC = 8 - 3 = 4

Dt_AC= 5h

Deslocamento (DS): DS = S - S₀

DS_AC = 310 - 10 = 300

DS_AC = 300km

Fonte: www.mundovestibular.com.br

www.vestibulandoweb.com.br/
www.passeiweb.com/
www.fisicaevestibular.com.br/

Questões resolvidas sobre velocidade escalar média

1) A velocidade escalar média de um automóvel é de 80km/h no primeiro trecho de seu percurso e 60 km/h no trecho restante . os trechos são percorridos no mesmo intervalo de tempo. qual é a velocidade escalar média durante todo o percurso?

Solução:

Espaço do primeiro trecho:

$x_1=80t$

Espaço do segundo trecho:

$x_2=60t$

Velocidade escalar média:

$v=\frac{80t+60t}{t+t}$

$v=\frac{140t}{2t}$

$\boxed{v=70km/h}$

2) a velocidade escalar média de um móvel de um automóvel até a metade de seu percurso é 90 km/h.Determine a velocidade escalar média no percurso total. Ela é a média aritmética das velocidades escalares médias em cada trecho do percurso ?

Solução:

Tempo no primeiro percurso:

$t_1=\frac{0,5x}{90}$

Tempo no segundo percurso:

$t_2=\frac{0,5x}{60}$

Sabemos o tempo total do percurso:

$t=t_1+t_2$

$t=\frac{0,5x}{90}+\frac{0,5x}{60}$

$t=\frac{x}{72}$

Sabemos a distância total:

$d=0,5x+0,5x$

$d=x$

Calculando a velocidade escalar média:

$v=\frac{d}{t}$

$v=\frac{x}{\frac{x}{72}}$

$\boxed{v=72km/h}$

Média Aritmética:

$Ma=\frac{90+60}{2}=75km/h$

Não é a média !

3) (UNESP-SP) No primeiro trecho de uma viagem, um carro percorre uma distância de 500m, com velocidade escalar média de 90km/h. O trecho seguinte, de 100m, foi percorrido com velocidade escalar média de

72km/h. A sua velocidade escalar média no percurso total foi, em m/s, de:

a) 20 b) 22 c) 24 d) 25 e) 30

Solução:

Primeiro deve-se converter as velocidades.
Para passar de km/h para m/s é só multiplicar por 3,6

90 km/h = 25 m/s
72 km/h = 20 m/s

No primeiro trecho:
∆t = ∆S / Vm = 500 / 25 = 20 s.

No segundo trecho:
∆t = ∆S / Vm = 100 / 20 = 5 s.

Vm = ∆S total / ∆t total
Logo,
Vm = (500 + 100) / (20 + 5)

Vm = 24 m/s.

Letra C.

4) Após os cinco primeiros segundos, a velocidade escalar do atleta fica constante até o final da corrida. O atleta cruza a linha de chegada com uma velocidade escalar igual a:

a) 5 km/h b)10km/h c)18km/h d)36km/h e)72km/h

Solução:

S = S0 + v0.t + at²/2

S = 1,0t²

S0 = 0
V0.t = 0

a = 2 m/s² (pq 2/2 = 1,0)
t = 5s --> t² = 25 s

Equação da Velocidade:

V = V0 + a.t
V = 0 + 2.5 = 10 m/s

Então, depois dessa velocidade ele permanece com velocidade constante. Assim a aceleração é zero. Então, se a velocidade é constante, o valor dela será 10 m/s. Como ele quer em km/h é só multiplicar por 3,6 = 36 km/h.

5) (CPS- 011) Considere que Roberto, em suas caminhadas de 2 000 m para manter o seu condicionamento físico, desenvolva

uma velocidade média de 5 km/h.

O tempo gasto para percorrer esta distância é de

a) 12 min. b) 20 min. c) 24 min. d) 36 min. e) 40 min.

Solução:

V=ΔS/Δt --- 5=2/Δt --- Δt=2/5=0,4h --- Δt=0,4x60 = 24min
Letra C.

6) (UNESP-SP) Ao passar pelo marco “km 200” de uma rodovia, um motorista vê um anuncio com a inscrição : ABASTECIMENTO E RESTAURANTE A 30 MINUTOS”.

Considerando que esse posto de serviço se encontra junto ao marco “km 245” dessa rodovia, pode-se concluir que o anunciante prevê, para os carros que trafegam nesse trecho, uma velocidade média , em km/h, de:

a) 80 b) 90 c) 100 d) 110 e) 120

Solução:

ΔS= 245 – 200 --- ΔS=45km --- Δt=0,5h --- V_m=45/0,5 --- V_m=90km/h
Letra B.

7) (UFC) Uma partícula desloca-se sobre uma reta na direção x. No instante t_A = 1,0 s, a partícula encontra-se na posição A e no instante t_B = 6,0 s encontra-se na posição B, como indicadas na figura a seguir.

Determine a velocidade média da partícula no intervalo de tempo entre os instantes t_A e t_B.

Solução:

V_m=ΔS/ Δt=(S_B – S_A)/(t_B – t_A)=70 – (-40)/6,0 – 1,0 --- V_m=22m/s

8) (FUVEST-SP-010) Astrônomos observaram que a nossa galáxia, a Via Láctea, está a 2,5.10⁶ anos-luz de Andrômeda, a

galáxia mais próxima da nossa.

Com base nessa informação, estudantes em uma sala de aula afirmaram o seguinte:

I. A distância entre a Via Láctea e Andrômeda é de 2,5 milhões de km.

II. A distância entre a Via Láctea e Andrômeda é maior que 2.10¹⁹ km.

III. A luz proveniente de Andrômeda leva 2,5 milhões de anos para chegar à Via Láctea.

Está correto apenas o que se afirma em

Dado: 1 ano tem aproximadamente 3.10⁷ s.

a) I. b) II. c) III. d) I e III. e) II e III.

Solução:

I. Errada --- 1 ano-luz é a distância que a luz percorre em 1 ano, no vácuo, com velocidade c=3.10⁸m/s=3.10⁵km/s --- d = v t --- d = (3.10⁵ km/s)x(2,5.10⁶ anosx3.10⁷s/ano) --- d=2,25.10¹⁹ km.

II. Correta --- veja os cálculos efetuados no item anterior.

III. Correta.

9) (UECE) Dois trens de comprimento 60 m e 90 m correm em trilhos paralelos e em sentidos opostos. O trem menor move-se com o dobro da velocidade do maior, para um referencial fixo na Terra.. Uma pessoa no trem menor observa que o trem maior gasta 2 s para passar por sua janela. Determine a velocidade, em m/s, do trem menor.

Solução:

Sentidos opostos --- V_R=2V + V=3V --- parando o trem menor e consequentemente a pessoa, o trem maior de velocidade relativa 3V e comprimento 90m demora 2s na ultrapassagem --- 3V=90/2 --- V=15m/s (velocidade do trem maior) --- como o trem menor tem o dobro da velocidade --- V’=30m/s

10) (Unitau-SP) Uma motocicleta com velocidade escalar constante de 20 m/s, andando paralelamente à uma ferrovia, ultrapassa um

trem de comprimento 100 m que “caminha”, no mesmo sentido, com velocidade escalar constante de 15 m/s. Desconsiderando o tamanho da moto, a duração da ultrapassagem é:

a) 5 s b) 15 s c) 20 s d) 25 s

Solução:

VR=(20 – 15)=100/Δt --- Δt=20s -
Letra C.

11) (U. F. Juiz de Fora-MG) O motorista de um caminhão pretende fazer uma viagem de Juiz de Fora a Belo Horizonte, passando por Barbacena (cidade situada a 100 Km de Juiz de Fora e a 180 Km de Belo Horizonte). A velocidade máxima no trecho que vai de Juiz de Fora a Belo Horizonte é de 90 km/h. Determine qual o tempo mínimo de viagem de Juiz de Fora a Belo Horizonte, respeitando-se os limites de velocidade:

a) 4,25h

b) 3,25h

c) 2,25h

d) 3,50h

e) 4,50h

Solução:

Juiz de Fora a Barbacena = Δt 1 = 100/80 = 1,25h
Barbacena a BH = Δt 2 = 180/90 = 2h
JF a BH = Δt 1 + Δt 2 = 1,25 + 2 = 3,25h

12) (U.F.São Carlos – SP) Um trem carregado de combustível, de 120m de comprimento, faz o percurso de Campinas até Marília, com velocidade constante de 50 Km/h. Esse trem gasta 15s para atravessar completamente a ponte sobre o rio Tietê. O comprimento da ponte é:

a) 100m

b) 88,5m

c) 80m

d) 75,5m

e) 70m

Solução:

50 Km/h ÷ 3,6 = 13,8 m/s

Vm = L(trem) + L (ponte) / Δt

13,8 = 120 + L (ponte) / 15

13,8 . 15 = 120 + L (ponte)

207-120 = L (ponte)

L (ponte) = 87m

13) (FUVEST) Diante de uma agencia do INSS há uma fila de aproximadamente 100 m de comprimento, ao longo da qual se distribuem de maneira uniforme 200 pessoas. Aberta a porta, as pessoas entram, durante 30 s, com uma velocidade média de 1 m/s. Avalie:

a) o número de pessoas que entraram na agencia;

Solução:

d_total = 100 m
n = 200 pessoas
v_m = 1 m/s
Δt = 30 s

Cada pessoa ocupa
d = d_total/n = 100/200 = 0,5 m

Em 30 s a fila anda:
v_m = d_fila/Δt
d_fila = v_m . Δt
d_fila = 1 . 30 = 30 m

O número de pessoas que entraram:
n' = d_fila/d = 30/0,5 = 60 pessoas

b)o comprimento da fila que restou ao lado de fora.

Solução:

d = d_total - d_fila = 100 - 30 = 70 m

14) (FUVEST 2008) Dirigindo-se a uma cidade próxima, por uma autoestrada plana, um motorista estima seu tempo de viagem, considerando que consiga manter uma velocidade média de 90 km/h. Ao ser surpreendido pela chuva, decide reduzir sua velocidade média para 60 km/h, permanecendo assim até a chuva parar, quinze minutos mais tarde, quando retoma sua velocidade média inicial. Essa redução temporária aumenta seu tempo de viagem, com relação à estimativa inicial, em

a) 5 minutos.
b) 7,5 minutos.
c) 10 minutos.
d) 15 minutos.
e) 30 minutos.

Solução:v_m' = 60 km/h
Δt' = 15 min = 15/60 h = 0,25 h
d = ?

v_m' = d/Δt'
d = v_m' . Δt'
d = 60 . 0,25 = 15 km

v_m'' = 90 km/h
d = 15 km
Δt'' = ?

v_m'' = d/Δt''
Δt'' = d/v_m''
Δt'' = 15/90 ~ 0,17 h
Δt = Δt' - Δt'' = 0,25 - 0,17 = 0,08 h = 0,08 . 60 min ~ 5 min

15) Um carro viaja de uma cidade A a uma cidade B, distantes 200km. Seu percurso demora 4 horas, pois decorrida uma hora de viagem, o pneu dianteiro esquerdo furou e precisou ser trocado, levando 1 hora e 20 minutos do tempo total gasto. Qual foi a velocidade média que o carro desenvolveu durante a viagem?

Solução:

S=200km

t=4h

v=?

Mesmo o carro tendo ficado parado algum tempo durante a viagem, para o cálculo da velocidade média não levamos isso em consideração.

16) No exercício anterior, qual foi a velocidade nos intervalos antes e depois de o pneu furar? Sabendo que o incidente ocorreu quando faltavam 115 km para chegar à cidade B.

Solução:

Antes da parada:

S= 200-115=85km

t=1hora

v=?

Depois da parada:

S= 115km

t= 4h-1h-1h20min= 1h40min=1,66h (utilizando-se regra de três simples)

v=?

17) Um ônibus percorreu 20 km a 60 km/h e 60 km a 90 km/h. Determine a velocidade escalar média do ônibus nos 80 km percorridos. Considere que, em cada trecho, o ônibus sempre manteve velocidade constante.

Solução:

18) Um automóvel percorreu um trajeto ABC, de 2 Km da seguinte maneira: de A até B (1 Km) com a velocidade escalar de 40 Km/h e de B até C (1 Km) com a velocidade escalar de 60 Km/h. Calcule a velocidade escalar média no percurso de A até C.

Solução:

O tempo que ele levou para ir de A ate B vale

T = Espaço que andou / velocidade
T = 1 / 40 h

de B ate C o tempo foi:

T = 1 / 60 h

O tempo total foi de 1/40 + 1/60 = 3+2/120 = 5/120

Então a velocidade em todo percurso foi:

V = 2 / 5/120
V = 240/5
V = 48 km/h

19) Ao se deslocar do Rio de Janeiro a Porto Alegre, um avião percorre essa distância com velocidade média v no primeiro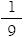

do trajeto e 2v no trecho restante.

A velocidade média do avião no percurso total foi igual a:

(A)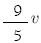

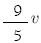
(B)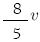

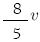
(C)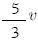

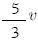
(D)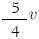

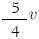
Solução:

A velocidade média corresponde à razão entre distância e tempo. Considerando a distância d entre as cidades, o intervalo de tempo t₁ gasto para percorrer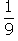

do trajeto, com velocidade média

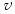, foi igual a:

Já o intervalo de tempo t₂, gasto para percorrer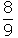

do trajeto, com velocidade média 2

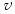, foi igual a:

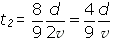
Assim, a velocidade média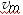

no percurso total d, em um intervalo de tempo t₁ + t₂, é dada por:

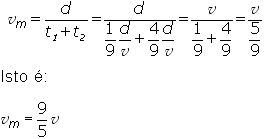
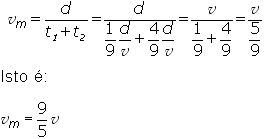
Percentual de acertos: 35,07%

20) Uma moto precisa realizar uma competição desenvolvendo uma velocidade escalar média de 100 km/h. na primeira metade a moto desenvolveu uma velocidade escalar média de 75 km/h. Qual deve ser a velocidade escalar média da moto, na segunda metade de seu trajeto, para conseguir seu intento?

Solução:

v1 = (∆s/2)/∆t1
∆t1 = (∆s/2)/v1
∆t1 = (∆s/2)/75
∆t1 = ∆s/150

v2 = (∆s/2)/∆t2
∆t2 = ∆s/(2 * v2)

Meta: --> velocidade média de 100 km/h
v = ∆s/∆t
100 = ∆s/∆t
∆t = ∆s/100

O tempo total é a soma do tempo gasto na 1ª metade com a 2ª metade:

∆s/100 = ∆s/(2 *v2 ) + ∆s/150
cortando o ∆s:

1/100 = 1/2*v2 + 1/150
3v = 150 + 2 v

v = 150 km/h

21)(UFAC) Um carro com uma velocidade de 80 km/h passa pelo km 240 de uma rodovia às 7 h 30 min. A que horas este carro chegará à próxima cidade, sabendo-se que a mesma está situada no km 300 dessa rodovia?

Resp: 8h 15 min

22) Um trem com comprimento 200 m gasta 20 s para atravessar um túnel de comprimento 400 m. Determine a velocidade escalar media do trem.

Resp: 30 m/s

23) (Cesgranrio-RJ) Uma patrulha rodoviária mede o tempo que cada veiculo leva para percorrer um trecho de 400 m da estrada. Um automóvel percorre a primeira metade do trecho com velocidade de 140 km/h. Sendo de 80 km/h a velocidade limite permitida, qual deve ser a maior velocidade média do carro na segunda metade do trecho para evitar ser multado?

Resp: 56 km/h

24) (PUC-SP 2010) Dois ciclistas partem simultaneamente de dois pontos distintos de uma estrada, distantes 24 km um do outro, e viajam em velocidades constantes; se seguirem no mesmo sentido, o mais rápido alcançará o outro após 2 horas; se seguirem um em direção ao outro, o encontro ocorrerá após 45 minutos. Assim sendo, a velocidade do ciclista mais rápido, em quilômetros por hora, é:

a) 16

b) 20

c) 22

d) 24

e) 28

25) Um automóvel viaja numa estrada retilínea, à velocidade de 30km/h. Depois, percorre mais 40km no mesmo sentido com uma velocidade de 60km/h. Qual a velocidade média do carro nesses 80km/ de viagem (suponha que o movimento é no sentido positivo do eixo x ) ?;

Resposta: 40 km/h

26) Uma tartaruga caminha, em linha reta, a 40 metros/hora, por um tempo de 15 minutos. Qual a distância percorrida?

a) 30 m

b) 10 km

c) 25 m

d) 1 km

e) 10 m