Cones
.jpg)
Outra forma de construir o cone é através da revolução do triângulo retângulo sobre um eixo vertical.
.jpg)
.jpg)
Elementos do cone .jpg)
.jpg)
g: geratriz do cone
h: altura do cone
r: raio da base
v: vértice
h: altura do cone
r: raio da base
v: vértice
Classificação do cone
Um cone é classificado segundo a inclinação do eixo VO:
- oblíquo: quando o eixo é oblíquo à base.
- reto: quando o eixo VO é perpendicular à base;

Todo cone reto pode ser obtido pela rotação de um triângulo em torno de um de seus catetos. Por isso o cone reto também é chamado de cone de revolução.
Observe que o cateto contido no eixo é a altura h do cone; o outro cateto é o raio da base R e a hipotenusa é a geratriz do cone. Observe, ainda, que, um cone reto, vale, pelo teorema de Pitágoras, a seguinte relação:
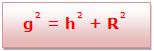
Observações
1. A seção meridiana de um cone reto é um triângulo isósceles que tem por base o diâmetro do cone e, por altura, a altura do cone. No caso particular de a seção meridiana ser um triângulo equilátero, o cone é chamado cone equilátero.
Áreas de um cone circular reto
Área da base
Por ser uma circunferência, a área da base de um cone é dada pela seguinte expressão:
Ab = π * R²
Área da lateral
A área lateral do cone é dada pela seguinte expressão:
Por ser uma circunferência, a área da base de um cone é dada pela seguinte expressão:
Ab = π * R²
Área da lateral
A área lateral do cone é dada pela seguinte expressão:
Al = π * r * g
Área total
É dada somando-se a área lateral e a área da base.
At = Al + Ab
At = π r (g+r)
At = π * R * (g + R)Área total
É dada somando-se a área lateral e a área da base.
At = Al + Ab
At = π r (g+r)
Exemplo:
Um cone circular reto tem 12 cm de raio e 16 cm de altura. Determinar a área lateral e a área total desse cone.

5) (Fuvest – SP) Um cone circular reto está inscrito em um paralelepípedo reto retângulo, de base quadrada, como mostra a figura.





6) Um cone possui diâmetro da base medindo 24 cm, geratriz 20 cm e altura igual a 16 cm. Determine sua área total e seu volume.


9) Qual é o volume de um cone circular reto, se a área da superfície lateral é 50π cm² e o raio da base mede 5 cm.
10) (UNIFOR-CE) Em um cone reto, a área da base é 9π cm² e a geratriz mede 3√10 cm. O volume desse cone, em centímetros cúbicos, é:
a) 27π b) 36π c) 48π d) 54π e) 81π
11) (UEMA) O volume de um cone equilátero que tem como área da base Ab = 12π m² é:
a) 72π m³ b) 24π m³ c) 36π m³ d) 28π m³ e) 40π m³
12) (UFPI) Se 8π cm² é a área lateral de um cone circular reto cujo raio da base é 2 cm, então a altura desse cone, em cm, é:
a) √2 b) √3 c) √6 d) 2√2 e) 2√3
13) (ITA-SP) Um prisma hexagonal regular tem como altura o dobro da aresta da base A. A razão entre o volume desse prisma e o volume do cone reto, nele inscrito, é igual a:
a) 6√2 / π b) 9√2 / π c) 3√6 / π d) 6√3 / π e) 9√3 / π
14) (MACKENSIE-SP) A planificação da superfície lateral de um cone é um semicírculo de raio 10√3. O volume do cone é:
a) 357π b) 573π c) 375π d) 537π e) 735π
Gabarito:
Solução:
Cálculo da geratriz:
g² = h² + r² ► g² = 16² + 12² ► g² = 400 ► g = 20
Cálculo da área lateral:
Al = πrg ► Al = π * 12 * 20 ► Al = 240π
A área lateral é 240π cm²
Cálculo da área total:
At = π*r (g + r) ► At = π * 12 * (20 + 12) ► At = 384π
A área total é 384π cm².
Volume de um cone
O volume do cone é dado pelo produto da área da base pela altura divido por três.
V = (Πr²h)/3
O volume do cone é dado pelo produto da área da base pela altura divido por três.
V = (Πr²h)/3

Exemplo:
Calcular o volume de um cone que tem 12 cm de altura, e o comprimento da circunferência de sua base é 8π cm.
Solução:
O comprimento de uma circunferência de raio r é dado por C = 2 π r.
Então: 2*π*r = 8π ► r = 4
V = 1/3 * π * 4² * 12 ► V = 64π
O volume é 64π cm³.
Exercícios resolvidos sobre cones
1) A geratriz de um cone circular reto mede 20 cm e forma um ângulo de 60 graus com o plano da base. Determinar a área lateral, área total e o volume do cone.
sen(60o) = h/20
(1/2) = h/20
= h/20
h = 10 R[3] cm
V = (1/3) Abase h
V = (1/3) π r2 h
(1/2)
h = 10 R[3] cm
V = (1/3) Abase h
V = (1/3) π r2 h
(1/3) π 102 10  = (1/3) 1000
= (1/3) 1000  π cm3
π cm3
r = 10 cm; g = 20 cm
Alat =π r g = π 10 20 = 200π cm2
Alat =π r g = π 10 20 = 200π cm2
Atotal = Alat + Abase
Atotal = π r g + π r2 = π r (r+g)
Atotal = π r g + π r2 = π r (r+g)
Atotal = π 10 (10+20) = 300π cm2
2. A hipotenusa de um triângulo retângulo mede 2cm e um dos ângulos mede 60 graus. Girando-se o triângulo em torno do cateto menor, obtem-se um cone. Qual é o seu volume?
g2 = h2 + R2
22 = h2 + 3
4 = h2 + 3
h = 1 cm
22 = h2 + 3
4 = h2 + 3
h = 1 cm
V = (1/3) Abase h = (1/3) Pi R2 h = (1/3) Pi 3 = Pi cm3
2) As áreas das bases de um cone circular reto e de um prisma quadrangular reto são iguais. O prisma tem altura 12 cm e volume igual ao dobro do volume do cone. Determinar a altura do cone.
hprisma = 12
Abase do prisma = Abase do cone = A
Vprisma = 2 Vcone
A hprisma = 2(A h)/3
12 = 2.h/3
h=18 cm
Abase do prisma = Abase do cone = A
Vprisma = 2 Vcone
A hprisma = 2(A h)/3
12 = 2.h/3
h=18 cm
3) Anderson colocou uma casquinha de sorvete dentro de uma lata cilíndrica de mesma base, mesmo raio R e mesma altura h da casquinha. Qual é o volume do espaço (vazio) compreendido entre a lata e a casquinha de sorvete?
V = Vcilindro - Vcone
V = Abase h - (1/3) Abase h
V = π R2 h - (1/3) π R2 h
V = Abase h - (1/3) Abase h
V = π R2 h - (1/3) π R2 h
V = (2/3) Pi R2 h cm3
4) Qual a altura de um cone circular reto cujo raio da base mede 5 cm e cuja geratriz mede 13 cm².
Solução:
g² = h² + r²
h² + 5² = 13²
h² = 144
h = 12 cm

A razão b a entre as dimensões do paralelepípedo é 3/2 e o volume do cone é π. Determine o comprimento g da geratriz do cone.
Solução:




6) Um cone possui diâmetro da base medindo 24 cm, geratriz 20 cm e altura igual a 16 cm. Determine sua área total e seu volume.
Solução:
Área total
A = π * r * (g + r)
A = 3,14 * 12 * (20 + 12)
A = 3,14 * 12 * 32
A = 1 205,76 cm²
A = π * r * (g + r)
A = 3,14 * 12 * (20 + 12)
A = 3,14 * 12 * 32
A = 1 205,76 cm²
Volume

7) Um cone possui raio da base medindo 4 cm e altura igual a 10 cm. Determine a altura de um líquido que ocupa nesse cone o volume de 100 cm³.
Solução:

8) A casquinha de um sorvete tem a forma de um cone reto. Sabendo que o raio da base mede 3cm e a
altura é de 12cm. Qual é o volume da casquinha? Resp. → V = 113,040m
Solução:
A base do cone é um círculo de área: Ab = πx r² ≈ 3,14 x 9 = 28,26cm². Como o volume da casquinha é dado por V = 1/3 x Ab x h = 1/3 x 28,26 x 12, temos: V ≈ 113,097cm³.
10) (UNIFOR-CE) Em um cone reto, a área da base é 9π cm² e a geratriz mede 3√10 cm. O volume desse cone, em centímetros cúbicos, é:
a) 27π b) 36π c) 48π d) 54π e) 81π
11) (UEMA) O volume de um cone equilátero que tem como área da base Ab = 12π m² é:
a) 72π m³ b) 24π m³ c) 36π m³ d) 28π m³ e) 40π m³
12) (UFPI) Se 8π cm² é a área lateral de um cone circular reto cujo raio da base é 2 cm, então a altura desse cone, em cm, é:
a) √2 b) √3 c) √6 d) 2√2 e) 2√3
13) (ITA-SP) Um prisma hexagonal regular tem como altura o dobro da aresta da base A. A razão entre o volume desse prisma e o volume do cone reto, nele inscrito, é igual a:
a) 6√2 / π b) 9√2 / π c) 3√6 / π d) 6√3 / π e) 9√3 / π
14) (MACKENSIE-SP) A planificação da superfície lateral de um cone é um semicírculo de raio 10√3. O volume do cone é:
a) 357π b) 573π c) 375π d) 537π e) 735π
Gabarito:
9) 125 √3π/3 10) A 11) B 12) E 13) D 14) C




A questão 7 tem um erro na solução. O raio não pode ser fixo. Ele varia de acordo com a altura do líquido.
ResponderExcluirverdade
Excluircomo fica a resposta certa da 7?
ExcluirNa questão 5 ñ entendi como deu a2b:12
ResponderExcluiruma questão que não consegui desenvolver sobre semicone é a seguinte :calcule a área lateral , a área total e o volume de um semicone com 3 cm de raio e 4 cm de altura.alguem pode me ajudar.bruxo-urussanga@hotmail.com
ResponderExcluirNão consegui desenvolver a questão 13! Alguém me ajuda, pf!!!
ResponderExcluirNão consegui desenvolver a questão 13! Alguém me ajuda, pf!!!
ResponderExcluirSOBRE A QUESTÃO 7
ResponderExcluirA altura da coluna de água é de 2,61cm aproximadamente