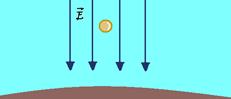
Campo Elétrico

seu centro. Um imã origina no espaço, ao seu redor um campo magnético  que faz surgirem forças sobre pedaços de ferro atraindo-os em sua direção. Uma carga elétrica Q origina no espaço ao seu redor um campo elétrico
que faz surgirem forças sobre pedaços de ferro atraindo-os em sua direção. Uma carga elétrica Q origina no espaço ao seu redor um campo elétrico  que faz surgirem forças sobre uma carga de prova q quando colocada no interior desse campo.
que faz surgirem forças sobre uma carga de prova q quando colocada no interior desse campo.
Vetor Campo Elétrico
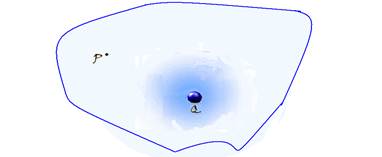
campo elétrico  em um ponto P do interior dessa região. Se você colocar em P pequenas cargas de prova q1, q2 e q3 verificará
em um ponto P do interior dessa região. Se você colocar em P pequenas cargas de prova q1, q2 e q3 verificará
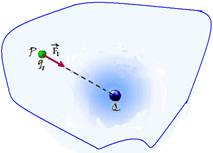
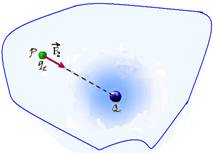
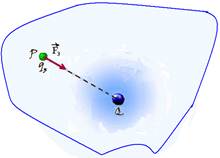
que sobre cada uma delas surgirão forças elétricas 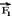 ,
, 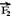 e
e 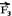 e que o quociente entre a força que atua sobre cada partícula e o respectivo módulo da mesma é sempre constante, ou seja:
e que o quociente entre a força que atua sobre cada partícula e o respectivo módulo da mesma é sempre constante, ou seja:
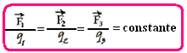
Observe que, se essa razão é constante, ela não depende dos valores de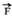 ou de q e que é característica do ponto que pertence ao campo elétrico. Então em cada ponto de um campo elétrico o vetor campo elétrico
ou de q e que é característica do ponto que pertence ao campo elétrico. Então em cada ponto de um campo elétrico o vetor campo elétrico 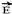 tem as seguintes características:
tem as seguintes características:

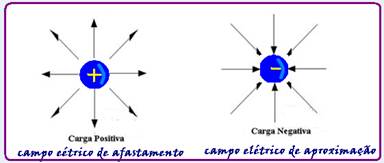
Campo elétrico gerado por uma
carga pontual Q
Verifique agora que a carga geradora Q>0 provoca em q2>0 localizado em N uma força de
repulsão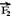 e, como q2 é positiva, campo e força têm mesma direção e mesmo sentido, estando
e, como q2 é positiva, campo e força têm mesma direção e mesmo sentido, estando 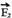 em N se afastando de Q>0. Generalizando: em qualquer ponto do campo gerado por Q>0 colocando-se cargas de prova positivas ou negativas, o campo
em N se afastando de Q>0. Generalizando: em qualquer ponto do campo gerado por Q>0 colocando-se cargas de prova positivas ou negativas, o campo
gerado será sempre de afastamento.
repulsão
gerado será sempre de afastamento.
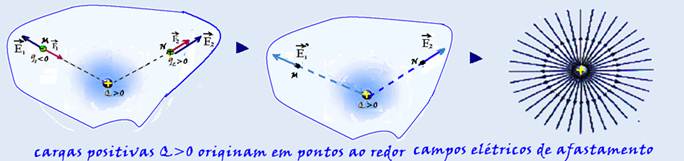
Analogamente, se a carga geradora fosse negativa Q<0, em todos os pontos o campo elétrico gerado seria de aproximação.

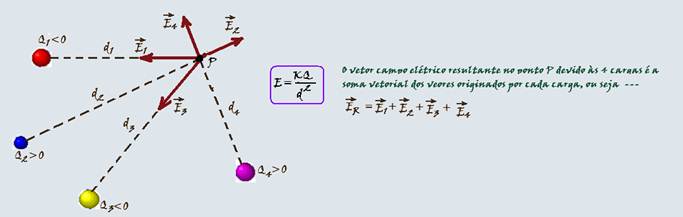
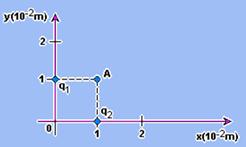
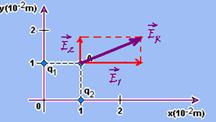
Campo elétrico gerado num ponto P
por várias cargas puntiformes

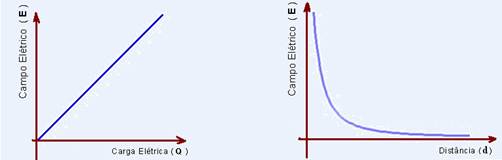
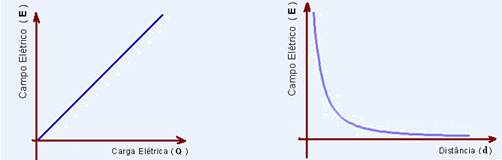
Gráficos do campo elétrico em
função de Q e de d
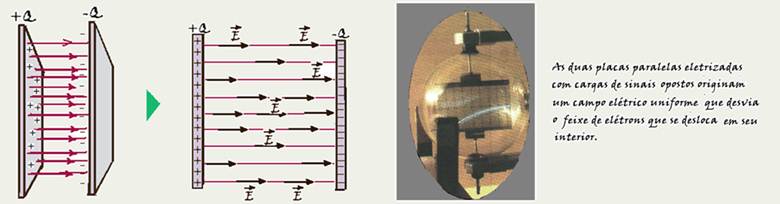
Campo elétrico uniforme
O que você deve saber


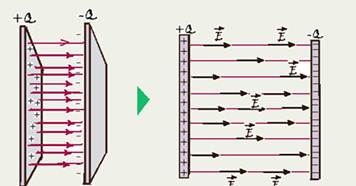
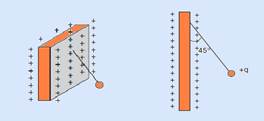
constante e é á permissividade elétrica do meio. Portanto, ao se colocar um isolante entre as placas, o campo elétrico entre elas varia. A figura abaixo ilustra um exemplo para duas placas carregadas com cargas de sinais opostos.
Potencial elétrico
Imagine um campo elétrico gerado por uma carga Q, ao ser colocada um carga de prova q em seu espaço de atuação podemos perceber que, conforme a combinação de sinais entre as duas cargas, esta carga q, será atraída ou repelida, adquirindo movimento, e conseqüentemente Energia Cinética.
Lembrando da energia cinética estudada em mecânica, sabemos que para que um corpo adquira energia cinética é necessário que haja uma energia potencial armazenada de alguma forma. Quando esta energia está ligada à atuação de um campo elétrico, é chamada Energia Potencial Elétrica ou Eletrostática, simbolizada por 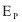 .
.
A unidade usada para a  é o joule (J).
é o joule (J).
Pode-se dizer que a carga geradora produz um campo elétrico que pode ser descrito por uma grandeza chamada Potencial Elétrico (ou eletrostático).
De forma análoga ao Campo Elétrico, o potencial pode ser descrito como o quociente entre a energia potencial elétrica e a carga de prova q. Ou seja:
Logo:
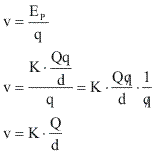
A unidade adotada, no SI para o potencial elétrico é o volt (V), em homenagem ao físico italiano Alessandro Volta, e a unidade designa Joule por coulomb (J/C).
Quando existe mais de uma partícula eletrizada gerando campos elétricos, em um ponto P que está sujeito a todas estes campos, o potencial elétrico é igual à soma de todos os potenciais criados por cada carga, ou seja:
Uma maneira muito utilizada para se representar potenciais é através de equipotenciais, que são linhas ou superfícies perpendiculares às linhas de força, ou seja, linhas que representam um mesmo potencial.
Para o caso particular onde o campo é gerado por apenas uma carga, estas linhas equipotenciais serão circunferências, já que o valor do potencial diminui uniformemente em função do aumento da distância (levando-se em conta uma representação em duas dimensões, pois caso a representação fosse tridimensional, os equipotenciais seriam representados por esferas ocas, o que constitui o chamado efeito casca de cebola, onde quanto mais interna for a casca, maior seu potencial).
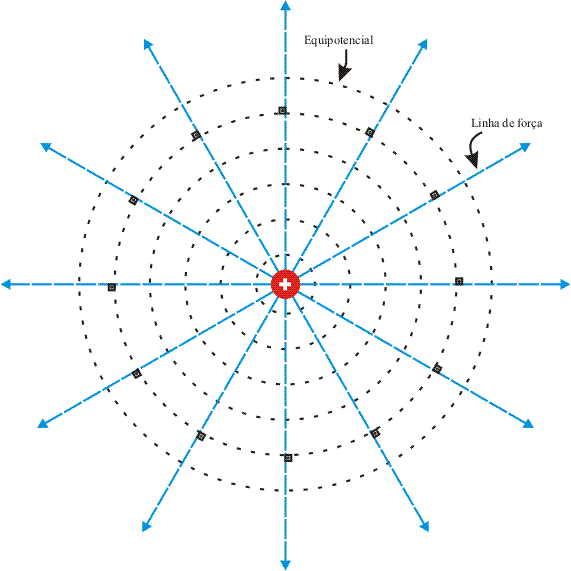
Trabalho de uma força elétrica
O trabalho 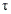 que uma carga elétrica realiza é análogo ao trabalho realizado pelas outras energias potenciais usadas no estudo de mecânica, ou seja:
que uma carga elétrica realiza é análogo ao trabalho realizado pelas outras energias potenciais usadas no estudo de mecânica, ou seja:
Se imaginarmos dois pontos em um campo elétrico, cada um deles terá energia potencial dada por:
Sendo o trabalho realizado entre os dois pontos:
Mas sabemos que, quando a força considerada é a eletrostática, então:
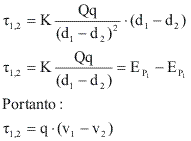
Diferença de potencial entre dois pontos
Considere dois pontos de um campo elétrico, A e B, cada um com um posto a uma distância diferente da carga geradora, ou seja, com potenciais diferentes. Se quisermos saber a diferença de potenciais entre os dois devemos considerar a distância entre cada um deles.
Então teremos que sua tensão ou d.d.p (diferença de potencial) será expressa por U e calculada por:
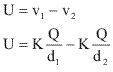
Questões resolvidas sobre Potencial elétrico
1) A figura mostra uma carga puntiforme Q e suas correspondentes superfícies equipotenciais vistas em corte. Uma outra carga puntiforme q é deslocada do ponto A para o ponto B, ambos mostrados na figura . Podemos concluir que o trabalho realizado pela força elétrica sobre a carga Q é : 
a) T > 0
b) T < 0 c) T indeterminado
d) T = 0
e) T só pode ser calculado se for conhecida a carga Q
2) (FESP) Considere as afirmações :
a) 5,0.10^-6
b) -5,0 .10^-6
c) 2,0.10^-5
d) -2,0 .10^-5
e) zero
I) Percorrendo-se uma linha de força no seu sentido, o potencial elétrico, ao longo de seus pontos, aumenta
II) As linhas de força são paralelas às superfícies equipotenciais
III) Num campo elétrico uniforme, as superfícies equipotenciais são esféricas e concêntricas
São corretas :
a) I
b) II
c) I e II
d) todas
e) nenhuma
3) (FEI - SP) A diferença de potencial elétrico entre dois pontos A e B é Va - Vb = 10 V. O trabalho realizado pela força elétrica no transporte de uma carga q = 2,0 Mc de A para B é, em joule :
a) 5,0.10^-6
b) -5,0 .10^-6
c) 2,0.10^-5
d) -2,0 .10^-5
e) zero
4) (PUC-SP) Assinale a afirmação FALSA :

a) k .Qq / d² e k . Qq / d
b) 2k.Qq / d² e 2k . Qq / d
c) zero e zero
d) 2k.Qq / d² e zero
e) zero e 2k .Qq / d
a) Uma carga negativa abandonada em repouso num campo eletrostático fica sujeita uma força que realiza sobre ela um trabalho negativo .
b) Uma carga positiva abandonada em repouso num campo eletrostático fica sujeita uma força que realiza sobre ela um trabalho positivo .
c) Cargas negativas abandonadas em repouso num campo eletrostático dirigem-se para pontos de potencial mais elevado .
d) Cargas positivas abandonadas em repouso num campo eletrostático dirigem-se para pontos de menor potencial .
e) O trabalho realizado pelas forças eletrostáticas ao longo de uma curva fechada é nulo.
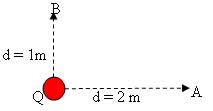
5) Duas cargas elétricas puntiformes Q estão fixas nos pontos A e B. Uma outra carga elétrica puntiforme q é colocada no ponto P, conforme a figura. Sendo k , a constante eletrostática do meio, pode-se concluir que a intensidade da força elétrica resultante que age em q e a energia potencial elétrica que q adquire valem, respectivamente :

a) k .Qq / d² e k . Qq / d
b) 2k.Qq / d² e 2k . Qq / d
c) zero e zero
d) 2k.Qq / d² e zero
e) zero e 2k .Qq / d
6) Sabe-se que a carga do próton = -carga do elétron = 1,6 .10^-19 C. Um próton tem velocidade relativa zero em relaçõão a um elétron. Para afastar um próton de um elétron, separados pela distância 10^ -15 m, é necessária uma energia :
a) da ordem de 10^-6 J
b) 1,6 .10^-14 J
c) 2,3 .10^-13 J
d) da ordem de 10^-7 j
e) nenhuma das anteriores
a) da ordem de 10^-6 J
b) 1,6 .10^-14 J
c) 2,3 .10^-13 J
d) da ordem de 10^-7 j
e) nenhuma das anteriores
7) Considere o campo elétrico orginado pelas cargas elétricas fixas +Q e -Q da figura.

Sejam Va, Vb e Vc oas potenciais elétricos nos pontos A, B e C, reaspectivamente. Pode-se afirmar que :
a) Va = 0; Vb > 0 e Vc < 0 b) Va = Vb = Vc = 0
c) Va = 0; Vb > 0 e Vc = 0
d) Va = Vb = 0 e Vc < 0 e) Va = 0; Vb > 0 e Vc > 0

Sejam Va, Vb e Vc oas potenciais elétricos nos pontos A, B e C, reaspectivamente. Pode-se afirmar que :
a) Va = 0; Vb > 0 e Vc < 0 b) Va = Vb = Vc = 0
c) Va = 0; Vb > 0 e Vc = 0
d) Va = Vb = 0 e Vc < 0 e) Va = 0; Vb > 0 e Vc > 0
8) (Cesgranrio) Nas figuras, três cargas positivas e pontuais q, são localizadas sobre a circuferência de um círculo de raio R de três maneiras diferentes. As afirmações seguintes se referem ao potencial eletrostático em O, centro da circuferência (o zero dos potenciais está no infinito);

I) O potencial em O nas figuras 1 e 3 é dirigido para baixo
II) O potencial em O tem o mesmo valor (não -nulo) nos três casos.
III) O potencial em O na figura 2 é nulo
Está(ão) certa(s) a(s) afirmação(ões):
a) I e II somente
b) II somente
c) III somente
d) I somente
e) I e III somente

I) O potencial em O nas figuras 1 e 3 é dirigido para baixo
II) O potencial em O tem o mesmo valor (não -nulo) nos três casos.
III) O potencial em O na figura 2 é nulo
Está(ão) certa(s) a(s) afirmação(ões):
a) I e II somente
b) II somente
c) III somente
d) I somente
e) I e III somente
9) (U.F.Uberlândia - MG) Duas cargas elétricas de mesmo módulo e de sinais opostos são colocadas a uma determinada distância. No ponto médio da reta que une as duas cargas, teremos :

a) o campo elétrico é nulo e o potencial elétrico não
b) o campo e o potencial elétricos são nulos
c) o potencial elétrico é nulo e o campo elétrico não
d) o potencial elétrico é numericamente duas vezes maior que a intensidade do campo elétrico
e) o campo e o potencial elétricos não são nulos
10) O potencial elétrico no ponto P médio de AB vale :

a) 9.10³
b) 18.10³
c) 36.10³
d) zero
e) nenhuma das anteriores
b) 18.10³
c) 36.10³
d) zero
e) nenhuma das anteriores
11) Suponhamos que uma carga elétrica seja deixada em um ponto A de um campo elétrico uniforme. Depois de percorrer uma distância igual a 20 cm, a carga passa pelo ponto B com velocidade igual a 20 m/s. Desprezando a ação da gravidade, calcule o trabalho realizado pela força elétrica no descolamento dessa partícula entre A e B. (Dados: massa da carga m = 0,4 g e q = 2 μC).







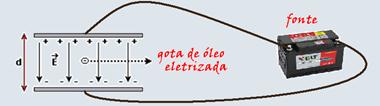


.gif)
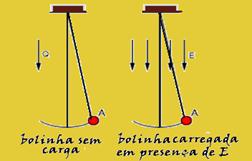
Determine o sinal e a carga elétrica que uma bolinha de gude, de massa 50g, deveria ter para permanecer suspensa em repouso, acima do solo. Considere o campo elétrico praticamente uniforme no local e despreze qualquer outra força atuando sobre a bolinha.
46) (UFPI) Uma carga de prova q, colocada num ponto de um campo elétrico E=2,0.103N/C, sofre ação de uma força F=18.10-5N. O valor dessa carga, em coulombs, é de:
a) 9.10-8
b) 20.10-8
c) 36.10-8
d) 9.10-2
e) 36.10-2
a) τ = 2,3 . 10-2 J
b) τ = 3,5 . 10-3 J
c) τ = 4 . 10-5 J
d) τ = 7 . 10-9 J
e) τ = 8 . 10-2 J
b) τ = 3,5 . 10-3 J
c) τ = 4 . 10-5 J
d) τ = 7 . 10-9 J
e) τ = 8 . 10-2 J
12) (UFSM-RS) Uma partícula com carga q = 2 . 10-7 C se desloca do ponto A ao ponto B, que se localizam numa região em que existe um campo elétrico. Durante esse deslocamento, a força elétrica realiza um trabalho igual a 4 . 10-3 J sobre a partícula. A diferença de potencial VA – VB entre os dois pontos considerados vale, em V:
a) -8 x 10-10
b) 8 x 10-10
c) -2 x 104
d) 2 x 104
e) 0,5 x 10-4
b) 8 x 10-10
c) -2 x 104
d) 2 x 104
e) 0,5 x 10-4
13) Determine a energia potencial elétrica de uma carga elétrica colocada em um ponto P cujo potencial elétrico é 2 x 104 V. Seja a carga igual a -6 μC.
a) -12 J
b) 0,012 J
c) -0,12 J
d) -12 x 10-6
e) 1,2 x 10-3 J
b) 0,012 J
c) -0,12 J
d) -12 x 10-6
e) 1,2 x 10-3 J
14) (UEPR) Um gerador funcionará em regime de potência útil máxima, quando sua resistência interna for igual:
a) à resistência equivalente do circuito que ele alimenta;
b) à metade da resistência equivalente do circuito que ele alimenta;
c) ao dobro da resistência equivalente do circuito que ele alimenta;
d) ao quádruplo da resistência equivalente do circuito que ele alimenta;
e) à quarta parte da resistência equivalente do circuito que ele alimenta.
15) (FCM SANTA CASA) Quando se aproximam duas partículas que se repelem, a energia potencial das duas partículas:
a) aumenta
b) diminui
c) fica constante
d) diminui e, em seguida, aumenta;
e) aumenta e, em seguida, diminui.
16) Uma carga elétrica de intensidade Q= +7µC gera um campo elétrico no qual se representam dois pontos, A e B. Determine o trabalho realizado pela força para levar uma carga 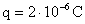 de um ponto ao outro (B até A), dada a figura abaixo:
de um ponto ao outro (B até A), dada a figura abaixo:
17) Qual é o potencial em um ponto C situado a 2 cm de uma carga elétrica de valor igual -4.10-8 C?
18) Qual é o potencial em um ponto A situado a uma distância d1 = 2 cm de uma carga elétrica Q1 = -8.10-9 C e a uma distância d2 = 6 cm de uma outra carga Q2 = 2.10-6 C?
Determine:
a) Os potenciais elétricos nos pontos A e B indicados.
b b) O trabalho da força elétrica que age numa carga q=1µC ao ser deslocada de A para B.
Adote referencial no infinito. É dado
Questões resolvidas sobre campo elétrico
20) (FACESP) Em uma certa região do espaço em que existe vácuo (constante eletrostática igual a 9 ⋅ 109Nm^2), estabeleceu-se um campo elétrico, cujo valor é 2 ⋅ 107N/C. A carga que o origina tem módulo 8μC. A que distância da carga essa medida de campo elétrico foi efetuada?
a) 1cm b) 6 cm c) 2,25cm d) 8 cm
21) (PUC-RIO 2008) Uma carga positiva puntiforme é liberada a partir do repouso em uma região do espaço onde o campo elétrico é uniforme e constante. Se a partícula se move na mesma direção e sentido do campo elétrico, a energia potencial eletrostática do sistema ...
A) aumenta e a energia cinética da partícula aumenta.
B) diminui e a energia cinética da partícula diminui.
C) e a energia cinética da partícula permanecem constantes.
D) aumenta e a energia cinética da partícula diminui.
E) diminui e a energia cinética da partícula aumenta.
22) As linhas de força permitem visualizar a configuração dos campos elétricos. Nos esquemas abaixo estão representadas algumas linhas de força.



O esquema que melhor representa a configuração do campo elétrico criado por um bipolo elétrico é o da alternativa:
(A) I (B) II (C) III (D )IV (E) V
23) (UEPG) Uma carga elétrica puntiforme Q gera um campo elétrico numa determinada região do espaço. Considerando um ponto P a uma distância r da carga Q, assinale o que for correto.
(01) A intensidade do vetor força elétrica que age sobre a carga de prova qo é inversamente proporcional à intensidade do vetor campo elétrico.
(02) O sentido do vetor campo elétrico é o do vetor força elétrica que age sobre a carga de prova qo, colocada no ponto P, se qo>0..
(04) A intensidade do vetor campo elétrico é inversamente proporcional ao quadrado da distância r.
(08) O campo elétrico será nulo no ponto P se a carga de prova qo tiver sinal contrário ao da carga Q.
(16) Se o sentido do vetor campo elétrico for de afastamento da carga Q, então a carga de prova qo tem sinal contrário ao da carga Q.
24) (UFRJ-RJ) Duas cargas puntiformes q1 = 2,0.10-6 C e q2 = 1,0.10-6 C estão fixas num plano nas posições dadas pelas coordenadas cartesianas indicadas a seguir. Considere K = 9,0.109 NC-2 m2.

Calcule o vetor campo elétrico na posição A indicada na figura, explicitando seu módulo, sua direção e seu sentido.
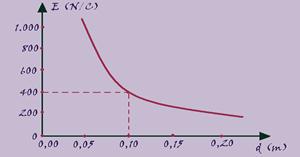
25) (FUVEST-SP) O diagrama da figura seguinte representa a intensidade do campo elétrico gerado por uma carga puntiforme fixa no vácuo, em função da distância d à carga. (Considere K=9,0.109 N.m2C2)

a) Calcule o valor da carga Q que origina o campo.
b) Determine a intensidade do campo elétrico em um ponto que dista 30cm da carga fixa.
b) Determine a intensidade do campo elétrico em um ponto que dista 30cm da carga fixa.
26) (MACKENZIE-SP) Existe um campo elétrico 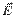 apontando para baixo, na atmosfera terrestre, com uma intensidade média de
apontando para baixo, na atmosfera terrestre, com uma intensidade média de

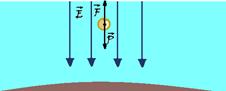
100 N/C. Deseja-se fazer flutuar nesse campo uma esfera de enxofre de 0,5 kg. Que carga (módulo e sinal) precisa ter a esfera? (g=10m/s2).
27) (MACKENZIE-SP-011)
A intensidade do vetor campo elétrico, em pontos externos, próximos a uma placa condutora eletrizada, no vácuo, é dada por
E = σ/εo. Nessa equação, σ é a densidade superficial de carga e εo, a constante de permissividade elétrica no vácuo. Uma pequena esfera, de massa 1,0g, eletrizada com carga q = +1,0μC, suspensa por um fio isolante, inextensível e de massa desprezível, mantém-se em equilíbrio na posição indicada.

Considerando-se que o módulo do vetor campo gravitacional local é g = 10m/s2, neste caso, a relação , referente
à placa, é
a) σ/εo = 1,0.102 V/m b) σ/εo = 2,0.102 V/m c) σ/εo = 1,0.104 V/m d) σ/εo= 2,0.104 V/m e) σ/εo = 1,0.106 V/m
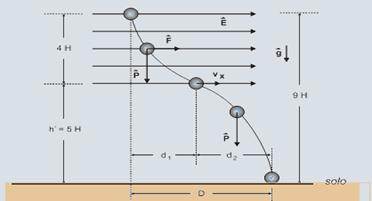
28) (UFC-CE-010) Uma partícula de massa m e carga elétrica q e largada do repouso de uma altura 9H, acima do solo. Do solo até uma altura h' = 5H, existe um campo elétrico horizontal de módulo constante E. Considere a gravidade local de modulo constante g, a superfície do solo horizontal e despreze quaisquer efeitos de dissipação de energia. Determine:
a) o tempo gasto pela partícula para atingir a altura h'.
b) o tempo gasto pela partícula para atingir o solo.
c) o tempo gasto pela partícula sob ação do campo elétrico.
d) o módulo do deslocamento horizontal da partícula, desde o instante em que a partícula é largada até o instante em que a partícula atinge o solo.
29) (ITA-SP-09) Uma partícula carregada negativamente está se movendo na direção +x quando entra em um campo elétrico uniforme atuando nessa mesma direção e sentido. Considerando que sua posição em t = 0 s é x = 0 m, qual gráfico representa melhor a posição da partícula como função do tempo durante o primeiro segundo?

30) (FUVEST-SP-09) Uma barra isolante possui quatro encaixes, nos quais são colocadas cargas elétricas de mesmo módulo, sendo as positivas nos encaixes claros e as negativas nos encaixes escuros. A certa distância da barra, a direção do campo elétrico está indicada na figura 1. Uma armação foi construída com quatro dessas barras, formando um quadrado, como representado na figura 2. Se uma carga positiva for colocada no centro P da armação, a força elétrica que agirá sobre a carga terá sua direção e sentido indicados por:
Desconsidere eventuais efeitos de cargas induzidas.

31) (UNICAMP-SP-09) O fato de os núcleos atômicos serem formados por prótons e nêutrons suscita a questão da coesão nuclear, uma vez que os prótons, que têm carga positiva q = 1,6.10-19 C , se repelem através da força eletrostática. Em 1935, H. Yukawa propôs uma teoria para a força nuclear forte, que age a curtas distâncias e mantém os núcleos coesos.
a) Considere que o módulo da força nuclear forte entre dois prótons FN é igual a vinte vezes o módulo da força eletrostática entre eles FE , ou seja, FN = 20 FE. O módulo da força eletrostática entre dois prótons separados por uma distância d é dado por FE = K(q2/d2), onde K = 9,0.109Nm2/C2. Obtenha o módulo da força nuclear forte FN entre os dois prótons, quando separados por uma distância = 1,6.10-15 m, que é uma distância típica entre prótons no núcleo.
b) As forças nucleares são muito maiores que as forças que aceleram as partículas em grandes aceleradores como o LHC. Num primeiro estágio de acelerador, partículas carregadas deslocam-se sob a ação de um campo elétrico aplicado na direção do movimento. Sabendo que um campo elétrico de módulo E = 2,0.105 N/C age sobre um próton num acelerador, calcule a força eletrostática que atua no próton.
32) (UEL-PR-09) Revistas de divulgação científica ajudam a população, de um modo geral, a se aproximar dos conhecimentos da Física. No entanto, muitas vezes alguns conceitos básicos precisam ser compreendidos para o entendimento das informações. Nesse texto, estão explicitados dois importantes conceitos elementares para a compreensão das informações dadas: o de campo elétrico e o de corrente elétrica.
Assinale a alternativa que corretamente conceitua campo elétrico.
a) O campo elétrico é uma grandeza vetorial definida como a razão entre a força elétrica e a carga elétrica.
b) As linhas de força do campo elétrico convergem para a carga positiva e divergem da carga negativa.
c) O campo elétrico é uma grandeza escalar definida como a razão entre a força elétrica e a carga elétrica.
d) A intensidade do campo elétrico no interior de qualquer superfície condutora fechada depende da geometria desta superfície.
e) O sentido do campo elétrico independe do sinal da carga Q, geradora do campo.
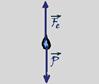
33) (FUVEST-SP) Um certo relógio de pêndulo consiste em uma pequena bola, de massa M = 0,1 kg, que oscila presa a um fio. O intervalo de tempo que a bolinha leva para, partindo da posição A, retornar a essa mesma posição é seu período To, que é igual a
2 s. Neste relógio, o ponteiro dos minutos completa uma volta (1 h) a cada 1800 oscilações completas do pêndulo. Estando o relógio em uma região em que atua um campo elétrico E, constante e homogêneo, e a bola carregada com carga elétrica Q, seu período será alterado, passando a TQ. Considere a situação em que a bolinha esteja carregada com carga Q = 3.10-5 C, em presença de um campo elétrico cujo módulo E = 1.105 V/m.

Então, determine:
a) a intensidade da força efetiva Fe, em N, que age sobre a bola carregada.
b) a razão R = TQ/To entre os períodos do pêndulo, quando a bola está carregada e quando não tem carga.
c) a hora que o relógio estará indicando, quando forem de fato 3 h da tarde, para a situação em que o campo elétrico tiver passado a atuar a partir do meio-dia.
b) a razão R = TQ/To entre os períodos do pêndulo, quando a bola está carregada e quando não tem carga.
c) a hora que o relógio estará indicando, quando forem de fato 3 h da tarde, para a situação em que o campo elétrico tiver passado a atuar a partir do meio-dia.
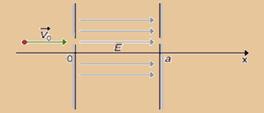
34) (FUVEST-SP) Uma partícula de carga q > 0 e massa m, com velocidade vo > 0, penetra numa região do espaço, entre x = 0 e x = a, em que existe apenas um campo elétrico uniforme, E > 0 (ver figura). O campo é nulo para x < 0 e x > a. Despreze as ações

gravitacionais.
a) Qual a aceleração entre x = 0 e x = a?
b) Qual a velocidade para x > a?
b) Qual a velocidade para x > a?
35)(PUC-MG) No início do século XX (1910), o cientista norte-americano ROBERT MILLIKAN conseguiu determinar o valor da carga elétrica do ELÉTRON como q = -1,6.10-19C. Para isso colocou gotículas de óleo eletrizadas dentro de um campo elétrico vertical, formado por duas placas eletricamente carregadas, semelhantes a um capacitor de placas planas e paralelas, ligadas a uma fonte de tensão conforme ilustração a seguir (g = 10 m/s2).

Admitindo que cada gotícula tenha uma massa de 1,6.10-25 kg, assinale o valor do campo elétrico necessário para equilibrar cada gota, considerando que ela tenha a sobra de um único ELÉTRON (carga elementar).
a) 1,6.103 N/C b) 1,0.105 N/C c) 2,0.105N/C d) 2,6.103N/C
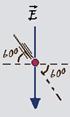
36) (UFV-MG) Em um campo elétrico variável e orientado para baixo, faz-se incidir um elétron, segundo um ângulo de 60o com a

horizontal. Desprezando a ação da gravidade, pode-se afirmar que a força elétrica que atua no elétron:
a) faz um ângulo de 0o com a horizontal.
b) tem a direção e o sentido do campo elétrico
c) faz um ângulo de 90o com a horizontal
d) é perpendicular ao vetor velocidade do elétron
e) tem a direção e o sentido da velocidade do elétron.
37) (UFPEL-RS) O positron e a anti-particula do elétron, possuem a mesma massa porem com carga elétrica positiva +e. Sob a ação de um campo elétrico uniforme o positron sofre uma aceleração cujo modulo é a.
Ao quadruplicarmos a intensidade do campo elétrico, o positron sofrerá uma aceleração cujo módulo vale
a) a/2 b) a c) a/4 d) 4a e) 3a
38) (UFRJ-RJ) Duas cargas puntiformes q1 = 2,0.10-6 C e q2 = 1,0.10-6 C estão fixas num plano nas posições dadas pelas coordenadas cartesianas indicadas a seguir. Considere K = 9,0.109 NC-2 m2.

Calcule o vetor campo elétrico na posição A indicada na figura, explicitando seu módulo, sua direção e seu sentido.
39) (PUC-SP) Caracterize o campo elétrico capaz de equilibrar no ar, próximo ao solo, uma gota de óleo de 4.10-10g de massa
e carga q = +10 e (e = 1,6.10-19 C). (g = 10m/s2)
40) (UFRJ) Em um laboratório, um pesquisador colocou uma esfera eletricamente carregada em uma câmara na qual foi feito vácuo.
O potencial e o módulo do campo elétrico medidos a certa distância dessa esfera valem, respectivamente, 600 V e 200 V/m.
Determine o valor da carga elétrica da esfera.
Determine o valor da carga elétrica da esfera.
De acordo com as seguintes expressões para o campo e para o potencial elétricos
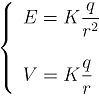
a distância para a qual o campo é igual a 200 V/m e o potencial é igual 600 V, corresponde a:
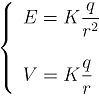
a distância para a qual o campo é igual a 200 V/m e o potencial é igual 600 V, corresponde a:
41) Num ponto de um campo elétrico, o vetor campo elétrico tem direção horizontal, sentido da direita para esquerda e intensidade Coloca-se, nesse ponto, uma carga
Coloca-se, nesse ponto, uma carga
 Coloca-se, nesse ponto, uma carga
Coloca-se, nesse ponto, uma carga
puntiforme de -2µC. Determine a intensidade, a direção e o sentido da força que atua na carga.
42) Uma carga positiva encontra-se numa região do espaço onde há um campo elétrico dirigido verticalmente para cima. Podemos afirmar que a força elétrica sobre ela é:
(A) para cima.
(B) para baixo.
(C) horizontal para a direita.
(D) horizontal para a esquerda.
(E) nula.
43) Numa certa região da Terra, nas proximidades da superfície, a aceleração da gravidade vale 9,8m/s² e o campo eletrostático do planeta (que possui carga negativa na região) vale 100 N/C.
.gif)
Determine o sinal e a carga elétrica que uma bolinha de gude, de massa 50g, deveria ter para permanecer suspensa em repouso, acima do solo. Considere o campo elétrico praticamente uniforme no local e despreze qualquer outra força atuando sobre a bolinha.
44) Determine as características de um campo elétrico, cuja carga de prova é igual a -6 μC, sujeita a uma força cuja intensidade é de 12N.
45) Uma carga de 2 C, está situada num ponto P, e nela atua uma força de 4N. Se esta carga de 2 C for substituída por uma de 3 C, qual será a intensidade da força sobre essa carga quando ela for colocada no ponto P?
a) 9.10-8
b) 20.10-8
c) 36.10-8
d) 9.10-2
e) 36.10-2
47) (FCC 2005- Adaptada) Considere uma carga elétrica puntiforme positiva q, fixa na origem de um sistema de eixos cartesianos e dois pontos, A e B, desse plano, como mostra a figura abaixo.
No ponto A, o vetor campo elétrico tem intensidade E. No ponto B, o valor dessa grandeza é,
(A) 4E
(B) 2E
(C) E
(D) E/4
(E) E/2
(B) 2E
(C) E
(D) E/4
(E) E/2
48) (MACKENZIE –SP) Considere a figura abaixo:
As duas cargas elétricas puntiformes Q1e Q2 estão fixas, no vácuo, onde Ko=9.109N.m2/C2 respectivamente, sobre pontos A e B. O campo elétrico resultante no ponto P tem intensidade:
a) zero
b) 4,0.105N/C
c) 5,0.105N/C
d) 9,0.105N/C
d) 9,0.105N/C
e) 1,8.106N/C
As duas cargas elétricas puntiformes Q1e Q2 estão fixas, no vácuo, onde Ko=9.109N.m2/C2 respectivamente, sobre pontos A e B. O campo elétrico resultante no ponto P tem intensidade:
a) zero
b) 4,0.105N/C
c) 5,0.105N/C
d) 9,0.105N/C
d) 9,0.105N/C
e) 1,8.106N/C
49) Determine o potencial elétrico resultante em P nos casos (A) e (B) indicados. Admita, em cada caso, que Q = 10^-6 C e d = 0,3 m . O meio é o vácuo
( Dado : k = 9.10^9)

A) O potencial elétrico num ponto P do campo é a soma dos potenciais produzidos em cada ponto .
B) Nesse caso temos uma carga positiva e outra negativa, e como o potencial elétrico é uma grandeza escalar, eles serão usadas com seus respectivos sinais .
Sabendo que o potencial em A = 100 V e em B = 80 V. Determine :
A) A intensidade E do campo elétrico
B) O potencial elétrico do ponto C
C) O trabalho da força elétrica que atua em q = 1Mc, ao ser deslocada de A para C
( Dado : k = 9.10^9)

A) O potencial elétrico num ponto P do campo é a soma dos potenciais produzidos em cada ponto .
B) Nesse caso temos uma carga positiva e outra negativa, e como o potencial elétrico é uma grandeza escalar, eles serão usadas com seus respectivos sinais .
50) São dadas as linhas de força e as superfícies eqüipotenciais de um campo elétrico uniforme.
Sabendo que o potencial em A = 100 V e em B = 80 V. Determine :
A) A intensidade E do campo elétrico
B) O potencial elétrico do ponto C
C) O trabalho da força elétrica que atua em q = 1Mc, ao ser deslocada de A para C
Gabarito:
1) Letra D. No ponto A e B temos o mesmo potencial elétrico, por estarem situados a mesma distância de Q . Como Va = Vb , sendo trabalho T = q ( Va – Vb)
Temos que T = 0
2) Letra C. O I é falso porque o potencial elétrico ao percorrer uma linha de força no seu sentido, ele diminui . O II é falso porque as linhas de força são perpendiculares às superfícies equipotenciais . E o III também é falso, porque num campo elétrico uniforme as superfícies equipotenciais são planos paralelos entre si .
3) Letra C. A fórmula do trabalho da força elétrica é T = q . (Va – Vb) , T = 2Mc . 10 , T = 2.10^-6 .10 , T = 2.10^-5 J
4) Letra A. Propriedades do Potencial Elétrico . Uma carga elétrica em repouso num ponto campo elétrico, fica sujeita a uma força elétrica resultante F e desloca-se espontaneamente. F realiza trabalho positivo .
5) Letra E. A força elétrica do ponto A em relação ao ponto P é Fe1 = k . Q.q / d² .
A força elétrica do ponto B em relação ao ponto P é Fe2 = k .Q.q / d² . Perceba que Fe1 = Fe2 . Logo , a força elétrica resultante em P é F resul = Fe1 – Fe2 ,
logo F resul = 0 . E a energia potencial elétrica tem fórmula no ponto A Ep = q.Va e no ponto B Ep = q.Vb,
sendo Va = k.Q / d e Vb = k.Q / d. Ep = q.Va + q.Vb . Logo Ep = 2k . Q.q / d
6) Letra C. Va = 9.10^9 .1,6.10^-19 / 10^-15 , Va = 14,4 .10^-10 / 10 ^-15
Va = 14,4 . 10^15 . A energia que atua é a potencial elétrica, Ep = q . Va .
E = 14,4 .10^5 .1,6 .10^-19
Ep = 23 . 10^-14 Ep = 2,3 .10^-13 . Logo, a energia necessária é 2,3 .10^-13 Joule
7) Letra D. Semelhante as questões anteriores. Potencial elétrico no campo de várias cargas . No ponto A temos duas cargas de sinais contrários e mesmo módulo (intensidade) separados à mesma distância do ponto, usando as fórmulas do potencial , encontramos que Va = 0 . E no ponto B, semelhante ao raciocínio do ponto A , temos Vb = 0 . No ponto C , a intensidade da carga – Q é maior , logo Vc < 0 .
8) Letra B. A I) é falsa porque potencial elétrico é uma grandeza escalar, logo não tem direção e sentido . A II) é verdadeiro , já que as cargas por terem mesmo valor e estarem a mesma distância de O terão mesmo potencial elétrico. O III) é falso , já que existe potencial elétrico da carga q em relação ao ponto O
9) Letra C. Potencial elétrico é uma grandeza escalar logo o sinal da carga importa , já o campo elétrico é uma grandeza vetorial, só utiliza o valor da carga, não usa o sinal . Como a questão fala que as cargas tem mesmo módulo, porém de sinais contrários, temos que o potencial elétrico é nulo e o campo elétrico não.
10) Letra D. Temos que em A o potencial elétrico é positivo e em B é negativo . O valor de
Va = 9.10³ e Vb = - 9.10³ . Como Vp = Va + Vb , Vp = 0 .
11) Letra E. Pelo teorema da energia cinética, temos:
τA→B=∆EC
Como a única força que age sobre a partícula durante todo o percurso de A até B é a força elétrica, e a energia cinética no ponto A é zero, temos:
τA→B=∆EC
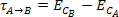
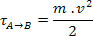
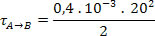
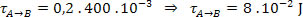
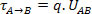
Como o exercício pede a diferença de potencial e nos fornece outros dados, temos:
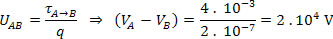
13) Letra C. Para calcular o valor da energia potencial elétrica basta multiplicar o valor do potencial elétrico pela carga elétrica. Assim temos:
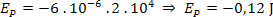
14) Letra A.
15) Letra A.
16) Primeiramente precisamos calcular o potencial elétrico em cada ponto, através da equação:
Em A:

Em B:
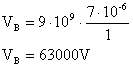
Conhecendo estes valores, basta aplicarmos na equação do trabalho de uma força elétrica:
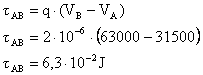
Distância = d = 2 cm = 0,02 m.
Carga = Q = -5.10-8 C.
Constante eletrostática no vácuo = K = 9.109 N.m2/C2.
A fórmula do potencial elétrico gerado por uma carga puntiforme:
Descrição do fenômeno: a carga elétrica -Q (chamada carga fonte), cria ao seu redor um campo elétrico. Dentro desse campo consideremos um ponto qualquer e o chamaremos de C. Queremos saber o potencial elétrico nesse ponto. Veja a figura:
Substituindo os valores dados na fórmula:
Portanto,
Como a carga fonte é negativa (Q<0) o potencial também será negativo (V<0).
➠ Dica: O potencial elétrico depende do referencial, sendo considerado nulo (V=0) o potencial de um ponto infinitamente afastado da carga fonte. O potencial elétrico em um ponto P não depende da carga de prova (q) - vamos provar que isso é verdade mais adiante.
O POTENCIAL ELÉTRICO GERADO POR DUAS CARGAS PUNTIFORME
18) Precisamos transformar a distância (d1) que está em centímetros (cm) para metros (m):
Distância = d1 = 2 cm = 0,02 m.
Carga = Q1 = -8.10-9 C.
Constante eletrostática no vácuo = K = 9.109 N.m2/C2.
Fórmula do potencial elétrico no ponto A gerado pela carga puntiformeQ1:
Descrição do fenômeno: Cada carga elétrica, Q1 e Q2, cria ao redor de si um campo elétrico. Queremos calcular o potencial elétrico total, em um ponto qualquer chamado de A, oriundo de cada carga fonte. Veja a figura:
Substituindo os valores dados na fórmula:
Portanto,
Como a carga fonte é negativa (Q1<0) o potencial é negativo (V1<0).
Cálculo do potencial parcial V2.
Precisamos transformar a distância (d2) que está em centímetros (cm) para metros (m):
Distância = d2 = 6 cm = 0,06 m.
Carga = Q2 = 2.10-6 C.
Constante eletrostática no vácuo = K = 9.109 N.m2/C2.
Fórmula do potencial elétrico gerado pela carga puntiforme Q2:
Substituindo os valores dados na fórmula:
Portanto,
Como a carga fonte é positiva (Q>0) o potencial é positivo (V>0).
O potencial total no ponto A será:
Portanto,
Desse modo
equivale a
➠ Dica: para obtermos o potencial em um ponto Pqualquer, situado no campo de várias cargas puntiformes, calculamos o potencial oriundo de cada fonte e, a seguir, faz-se a soma algébrica dos potenciais obtidos.
Em A temos:
b) O trabalho da força elétrica é:
20) Letra B.
Q = 8 × 10–6C
E = 2 × 107N/C
E = K ⇒ 2 × 107 = 9 × 109 ⋅8 . 10 ^ - 6 / r² = 36 × 10^-4 ⇒ r = 6 × 10^-2 m = 6 cm
21) Letra E.
22) Letra B
23) 01. Falsa --- E=F/qo --- observe nessa expressão qo=E/F que E e F são diretamente proporcionais.
02. Verdadeira --- veja teoria.
04. Verdadeira --- E=KQ/d2.
08. Falsa --- terá sentido contrário ao da força elétrica.
16. Falsa --- veja teoria
24) Sendo a distância do ponto A a cada uma das cargas iguais e q1=2q2 você observa que E1=2E2 --- E1=Kq1/(1.10-2)2 ---

E1=9.109.2.10-6/1.10-4 --- E1=18.107N/C --- E2=9.107N/C --- ER2=E12+ E22 --- ER2=(18.107)2 + (9.107)2 --- intensidade -ER=9√5.107N/C --- direção - tgα=E2/E1=1/2, sendo α o ângulo que ER forma com o eixo x --- sentido - se afastando da origem a partir do ponto A.
25) a) Quando E=400N/C – d=0,10m --- E=KQ/d2 --- 400=9.109.Q/(10-1)2 --- Q=4.102.10-2/9.109 --- Q≈0,45.10-9C ---
Q ≈ 4,5.10-10 C
b) E=KQ/d2=9.109.4,5.10-10/(3.10-1)2 --- E=40,5.10-1/9.10-2 --- E=4,5.10 --- E=45 N/C
26) A carga deve ter sinal negativo para que a força elétrica seja contrária ao campo elétrico e possa equilibrar a força peso ---

P=m.g=0,5.10 --- P=5N --- E=F/q --- 100=F/q --- 100=P/q+ --- 100=5/q --- q=5.10-2 C
27) 

28) Como o campo elétrico (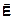 ) é horizontal, e a força elétrica (
) é horizontal, e a força elétrica (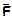 ) só age na direção do campo, ela não influi no tempo de queda --- como o enunciado não informou o sinal da carga, considere-a positiva --- por isso, a força elétrica está no mesmo sentido do campo elétrico.
) só age na direção do campo, ela não influi no tempo de queda --- como o enunciado não informou o sinal da carga, considere-a positiva --- por isso, a força elétrica está no mesmo sentido do campo elétrico.

a) Como indicado na figura, quando a partícula atingir a altura h’ = 5 H, ela terá caído 4 H --- como na vertical o movimento é uniformemente variado --- 4 H = 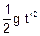 Þ 8 H = g t’ 2 Þ
Þ 8 H = g t’ 2 Þ 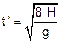 .
.
b) Analogamente ao item anterior, para o tempo total --- 9 H = 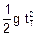 Þ 18 H = g
Þ 18 H = g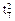 Þ
Þ 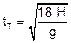
c) o tempo que a partícula permanece sob ação do campo elétrico é 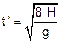
d) A distância horizontal percorrida pela partícula, como mostrado na figura é --- D = d1 + d2 (I) --- distância horizontal d1 é percorrida em movimento uniformemente acelerado pela ação do campo elétrico, durante o tempo t’ --- aceleração horizontal da partícula --- F = m ax --- q E = m ax --- ax = 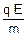 --- então --- d1 =
--- então --- d1 = 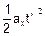 --- d1 =
--- d1 = 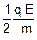
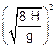 --- d1 =
--- d1 = 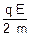
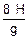 --- d1 = 4
--- d1 = 4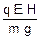 (II)
(II)
A partir daí, o movimento da partícula é um lançamento oblíquo para baixo, sob ação exclusiva do campo gravitacional. O tempo para atingir o solo é --- t2 = tT – t’ Þ t2 =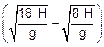 (III) --- ao abandonar o campo elétrico, a velocidade horizontal da partícula é vx, como indicado na figura, adquirida durante o tempo (t’) em que sofreu ação do campo elétrico, sendo, então --- vx = ax t’ Þ vx =
(III) --- ao abandonar o campo elétrico, a velocidade horizontal da partícula é vx, como indicado na figura, adquirida durante o tempo (t’) em que sofreu ação do campo elétrico, sendo, então --- vx = ax t’ Þ vx = 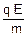
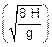 (IV)
(IV)
A distância horizontal d2 é percorrida em movimento uniforme, com a velocidade vX durante o tempo t2 --- assim, de (III) e (IV) vem ---
d2 = vx t2 Þ d2 = 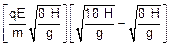 --- aplicando a distributiva --- d2 =
--- aplicando a distributiva --- d2 = 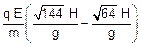 --- d2 =
--- d2 = 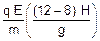 --- d2 = 4
--- d2 = 4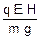 (V) --- substituindo (II) e (V) em (I) --- D = 4
(V) --- substituindo (II) e (V) em (I) --- D = 4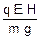 + 4
+ 4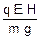 --- D = 8
--- D = 8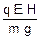 .
.
29) Letra E. Se a partícula é carregada negativamente e está se movendo na direção e sentido do campo elétrico existe uma força constante de sentido oposto atuando sobre a partícula. Desta forma a partícula apresentará uma aceleração constante e negativa, o que está caracterizado no diagrama de aparência parabólica de concavidade para baixo
30) Letra B. A carga positiva colocada em P será mais repelida pelo canto superior direito do que pelo canto inferior esquerdo. Além disso, será mais atraída pelo canto superior esquerdo do que pelo canto inferior direito. Assim a resultante deverá estar apontando para a esquerda
31) a) FN=20FE=20Kq2/d2=20.9.109.(1,6.10-19)2/1,6.10-15)2 --- FN=180.109.10-8 --- FN=1.800N --- FN=1,8.103N
b) F = q.E = 1,6.10-19.2.106 = 3,2.10-13 N
32) Letra A
33) 

34) a) F=ma --- qE=ma --- a=qE/m
b) Torricelli --- V2 = Vo2 + 2.a.ΔS --- V2=Vo2 + 2.qE/m.a --- V=√(Vo2 + 2.q.(E/m).a)
35) gota em equilíbrio --- FR=0 --- F=P --- q.E=m.g --- 1,6.1019.E=1,6.10-25.10 --- E=1,6.10-19/1,6.10-24 --- E=1,0.105 N/C
36) Letra C. A direção e o sentido do a força elétrica estão relacionadas com a direção e o sentido do campo elétrico, no caso a força elétrica é vertical e para cima (elétron tem carga negativa)
37) Letra D. E=F/q --- E=ma/q --- nesta expressão, como a massa e a carga são constantes, se você quadruplicar a intensidade do campo elétrico você estará quadruplicando a aceleração
38) Sendo a distância do ponto A a cada uma das cargas iguais e q1=2q2 você observa que E1=2E2 --- E1=Kq1/(1.10-2)2 ---

E1=9.109.2.10-6/1.10-4 --- E1=18.107N/C --- E2=9.107N/C --- ER2=E12+ E22 --- ER2=(18.107)2 + (9.107)2 --- intensidade -ER=9√5.107N/C --- direção - tgα=E2/E1=1/2, sendo α o ângulo que ER forma com o eixo x --- sentido - se afastando da origem a partir do ponto A.
39) O campo elétrico deve ter direção vertical e sentido para cima, pois a carga é positiva e a força deve também ser para cima
para anular a força peso que é vertical e para baixo --- Fe=P --- q.E=m.g --- 10.1,6.10-19.E=4.10-10.10-3.10 ---
E=4.10-12/16.10-9 --- E=0,25.10-3 N/C --- E=2,5.10-4 N/C, direção vertical e sentido para cima.
40) 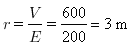
Assim, o valor da carga elétrica é dado por:
41) A força que atua na carga tem:
.gif)
.gif)
.gif)
q =18.10-5/2.103
q = 9 . 10-8 C
Intensidade:
Direção: horizontal
Sentido: da esquerda para direita.
42) Letra A. A força exercida sobre uma carga positiva tem o mesmo sentido do campo
43)
.gif)
44)
.gif)
45)
.gif)
46) Letra A.
E = F/q
q = F/Eq =
q = 9 . 10-8 C
47) Campo elétrico no ponto A
dA2 = (32 + 42) = (9 + 16) = 25EA = E = K.q/dA2 = K.q/25 → Kq = 25E
Campo elétrico no ponto BEB = K.q/dB2 = 25E/102 = 25.E/100 = E/4
48) E = K.Q/d2
E1 = 9.109. 4.10-6/(2.10-1)2 = 9.105 N/CE2 = 9.109. 1.10-4/12 = 9.105 N/C
ER = 9.105 - 9.105 = 0
49) A) O potencial elétrico num ponto P do campo é a soma dos potenciais produzidos em cada ponto .
Logo , Vp = k. Q / d + K.Q / dVp = 9.10^9 .10^-6 / 0,3 + 9.10^9 . 10^-6 / 0,3
Vp = 6 . 10^4
B) Nesse caso temos uma carga positiva e outra negativa, e como o potencial elétrico é uma grandeza escalar, eles serão usadas com seus respectivos sinais .
Logo,
Vp = k . Q / d + k . – Q / d
E encontramos que Vp = 0
50) A) A ddp significa a diferença de potencial, logo, Va – Vb = E.d. Sendo Va = 100V e Vb = 80V e d = 0,1m , vem :
100 – 80 = E . 0,1E = 200 V/ m
Note que o potencial vai diminuindo ao percorrer uma linha de força .
B) Para o cálculo do potencial elétrico no ponto C (Vc) podemos novamente usar Va – Vb = E.d
Sendo Vb = 80, E = 200 V / m e d = 0,2 m , temos :
80 – Vc = 200.0,2
Vc = 40 V
C) O trabalho da força elétrica que atua em q no deslocamento de A até C é dado por :
Tac = q (Va – Vc) , sendo q = 1Mc = 10^-6
Tac = 10^-6 (100 – 40)
Tac = 6.10^-5 J
Fontes: http://fisicaevestibular.com.br/exe_els_3.htm
http://exercicios.brasilescola.com/exercicios-fisica/exercicios-sobre-campo-eletrico-2.htm














se no caso eu tiver 0,9 N de força eletrica ela ficará 0,9.10-2 ou 9.10-2?
ResponderExcluirFicará 9 x 10 ^ -1
Excluirisso é o que mais me complica
ResponderExcluir