O conceito de momento (ou torque) é usado, mesmo intuitivamente, com grande frequência em nossa vida diária.
É o caso, por exemplo, de uma pessoa que fecha uma porta aplicando a força no meio da porta; obterá um efeito de rotação maior se aplicar a mesma força na extremidade da porta. Nessa última situação, a distância da força ao eixo de rotação é maior e, portanto, maior será o momento dessa força, isto é, maior será o efeito de rotação que ela produz.
Considerando um braço de alavanca de massa desprezível d = r com uma das extremidades fixa na origem de um sistema de referência conforme a figura 01.
Figura 01: representação do diagrama de forças que atuam sobre um objeto de massa m que será forçado a se movimentar em torno de um ponto fixo.
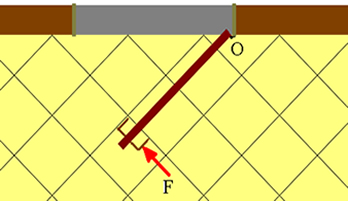
Consideremos que na extremidade de r há um corpo de massa m. Ao produto da força aplicada na extremidade d da alavanca pela distância da alavanca d e o seno do ângulo entre a linha sobre a qual está o braço de alavanca e a direção da força aplicada chamamos torque, ou momento de força. Um exemplo muito comum de torque é quando se aplica uma força perpendicular ao cabo de uma chave, fazendo-a girar um parafuso em torno de um ponto fixo, conforme na figura 02.
figura 02: representação de uma situação comum de aplicação de torque.
Matematicamente, o vetor torque τ é dado pelo produto vetorial entre os vetores r e F:
τ = rxF
Que equivale a:
τ = r.F.senθ
Onde τ é o torque;
r é a distância da força aplicada até o ponto fixo;
F é a força aplicada;
senθ é o seno do ângulo entre a força e o braço de alavanca d.
r é a distância da força aplicada até o ponto fixo;
F é a força aplicada;
senθ é o seno do ângulo entre a força e o braço de alavanca d.
Quando θ é 90º senθ = 1 então a equação se reduz a:
τ = F.r
Se considerarmos um braço de alavanca d com comprimento r, teremos:
τ = F.d em N.m (no SI)
observe que é a mesma dimensão de energia, porém a unidade de energia é o joule e é simbolizada por J, no SI.
Por exemplo, ao fechar a porta de um carro, de 0,9 m de comprimento, nota-se que esta gira no sentido horário. Sabendo que a força aplicada à porta é de 4 N, qual será o valor da intensidade do Torque em relação ao ponto fixo da porta?
Sabemos que o torque, quando o movimento é no sentido horário, é dado por:
T = - F . d
Sendo:
Sabemos que o torque, quando o movimento é no sentido horário, é dado por:
T = - F . d
Sendo:
d = 0,9m e F = 4 N
assim:
T = - 4 . 0,9
Portanto:
T = -3,6 N.m
Podemos concluir que o torque é inversamente proporcional à distância d em relação ao ponto de rotação. Devido a esse fato é que se coloca a maçaneta das portas na extremidade oposta ao ponto de rotação.
Fontes: www.infoescola.com/
www.brasilescola.com/
Questões resolvidas de vestibular sobre Momento de uma Força (Torque)
1) Em cada caso representado abaixo, calcule o momento da força aplicada na barra, em relação ao ponto O.
Obs.: Quando houver inclinação diferente de 90° entre F e a barra, usa-se a seguinte fórmula:
M = F. d .sen θ
a) M = F. d b) M = F. d. senθ
F=10 N F =8 N
d=b=2 m d=b=6 m
M = 10.2=20 θ=30° e sen 30°=0,5
M = 20 N.m M = 8.6.0,5 = 24
M = 24 N.m
Lembre-se que a unidade de medida do torque (momento) é N.m
F=10 N F =8 N
d=b=2 m d=b=6 m
M = 10.2=20 θ=30° e sen 30°=0,5
M = 20 N.m M = 8.6.0,5 = 24
M = 24 N.m
Lembre-se que a unidade de medida do torque (momento) é N.m
2) Uma barra homogênea AB de peso P = 10 N e comprimento L = 50 cm está apoiada num ponto O a 10 cm de A. De A pende um corpo de peso Q1 = 50 N. A que distância de x deve ser colocado um corpo de peso Q2 = 10 N para que a barra fique em equilíbrio na horizontal?
Solução:
O exercício falou sobre o peso da barra. Então não podemos desprezá-lo. Ele deve ser representado no centro da barra (veja a figura a seta azul). Observe também as distâncias das aplicações das forças até o ponto O.
A soma dos momentos deve ser zero:
Q1 provoca uma rotação na barra no sentido anti-horário (M<0) Q2 e P no sentido horário (M>0):
Solução:
A soma dos momentos deve ser zero:
Q1 provoca uma rotação na barra no sentido anti-horário (M<0) Q2 e P no sentido horário (M>0):
MQ2 + MP – MQ1 = 0
Q2.d2 + P . d – Q1.d1 = 0
10.(40-x) + 10.15 – 50.10=0
400-10x+150-500=0
- 10 x = 500 -150 -400
- 10 x = - 50 (multiplica por – 1)
10 x = 50
X = 50/10
X = 5 cm
3) (UFLA-95) A figura abaixo representa um sistema em equilíbrio estático. Sendo PA = 20 N, o peso PB deve ter valor de:
Dica: A soma dos momentos deve ser zero. O giro no sentido horário provoca momento positivo e no sentido anti-horário provoca momento negativo.
Quando temos objetos pendurados na barra ou sobre a barra, a força peso é a força aplicada perpendicularmente à barra. Observe a figura com os vetores das forças pesos representados em cada ponto de aplicação. O ponto onde a barra está apoiada está representado pelo triângulo.
As forças aplicadas são PA e PB .
Para o equilíbrio, a soma dos momentos deve ser zero:MPB – MPA = 0 (PA faz a barra girar sentido anti-horário em torno do ponto de apoio, logo o momento é negativo).
5) (UFV) Um rapaz de 900 N e uma garota de 450 N estão em uma gangorra. Das ilustrações abaixo, a que representa uma situação de equilíbrio é:
7) a) Calcule a distância horizontal (d), lembre F e d são perpendiculares.
b) Utilize M = F.d e verifique o sentido do momento.





As forças aplicadas são PA e PB .
Para o equilíbrio, a soma dos momentos deve ser zero:MPB – MPA = 0 (PA faz a barra girar sentido anti-horário em torno do ponto de apoio, logo o momento é negativo).
PA.dA – PB . dB = 0
20 . 3 – PB . 4 = 0 à 60 – 4.PB=0 à 4.PB = 60
PB = 60/4 = 15 N.m à PB = 15 N.m
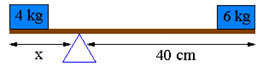
4) Vejamos a figura abaixo. Na figura temos dois blocos cujas massas são, respectivamente, 4 kg e 6 kg. A fim de manter a barra em equilíbrio, determine a que distância x o ponto de apoio deve ser colocado. Suponha que inicialmente o ponto de apoio esteja a 40 cm da extremidade direita da barra.

a) x = 60 cm
b) x = 20 cm
c) x = 50 cm
d) x = 30 cm
e) x = 40 cm
b) x = 20 cm
c) x = 50 cm
d) x = 30 cm
e) x = 40 cm
Solução:
Para que a barra se mantenha em equilíbrio o momento do conjunto tem que ser igual a zero.
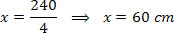
M1=M2
F1.d1=F2.d2
4 . x = 6 .40
F1.d1=F2.d2
4 . x = 6 .40
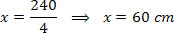
5) (UFV) Um rapaz de 900 N e uma garota de 450 N estão em uma gangorra. Das ilustrações abaixo, a que representa uma situação de equilíbrio é:
a)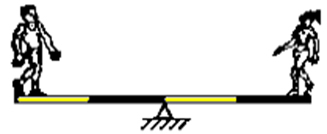

b)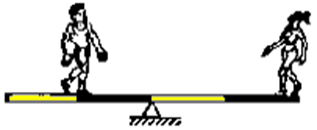

c)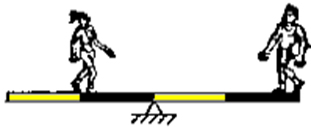

d)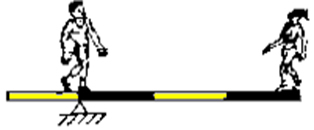

e)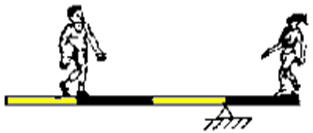

Solução:
Para resolver essa situação basta igualar os momentos, isto é, o momento de força do rapaz é igual ao momento de força da moça, ambos sobre a barra, portanto, temos:
Mrapaz=Mmoça
Fr.d1=Fm.d2
Fr.d1=Fm.d2
Como o peso do homem é o dobro do peso da moça, ele deve estar na metade da distância do apoio.
900 . 1 = 450 .2
6) Suponha que para fechar uma porta de 0,8 metros de largura, uma pessoa aplica perpendicularmente a ela uma força de 3 N, como mostra a figura abaixo. Determine o momento dessa força em relação ao eixo O.

a) M = -3,75 N.m
b) M = -2,4 N.m
c) M = -0,27 N.m
d) M = 3,75 N.m
e) M = 2,4 N.m
b) M = -2,4 N.m
c) M = -0,27 N.m
d) M = 3,75 N.m
e) M = 2,4 N.m
Solução:
Podemos ver pela figura que o momento dessa força será negativo, pois ela gira no sentido horário, portanto, temos que:
M = -F.d ⟹ M = -3 .0,8 ⟹ M = -2,4 N.m
Alternativa B
7) a) Calcule a distância horizontal (d), lembre F e d são perpendiculares.
b) Utilize M = F.d e verifique o sentido do momento.
Resolução:
a) Cálculo da distância d.

À distância d é o cateto oposto em relação ao ângulo de 30º.
d = 1 m.
b) M = F.d.
M = 10N.1 m
M = 10 N.m (sentido horário)
8) a) Projetar a força na direção horizontal e vertical.b
b) Utilize M = F.d e verifique o sentido do momento.
Resolução:
a) Projeção de FH e FV.

FH é o cateto oposto em relação ao ângulo q.

FH = 6 N como a FH e a distância são paralelos não há rotação;
FV é o cateto adjacente em relação ao ângulo q.

FV = 8 N
b) M = F.d.
M = 8N.4m
M = 32 N.m
9) A figura ilustra uma gangorra de braços iguais. Contudo as crianças A e B não estão sentadas em posições equidistantes do apoio. A criança A de 470 N de peso está a 1,5m do apoio. A criança B de 500 N de peso está a 1,6 m do apoio. O peso da haste da gangorra é de 100N. A gangorra vai:


9) A figura ilustra uma gangorra de braços iguais. Contudo as crianças A e B não estão sentadas em posições equidistantes do apoio. A criança A de 470 N de peso está a 1,5m do apoio. A criança B de 500 N de peso está a 1,6 m do apoio. O peso da haste da gangorra é de 100N. A gangorra vai:
a) descer no lado da criança A.
b) descer no lado da criança B.
c) ficar em equilíbrio na horizontal.
d) fazer uma força de 970 no apoio.
Solução:
As forças que atuam na gangorra são:
Força FA que a criança faz na gangorra de mesmo módulo que seu peso = 470 N
Força FB que a criança faz na gangorra de mesmo módulo que seu peso = 500 N
Peso da gangorra que atua no centro de massa (meio) = 100 N
Força de reação normal da gangorra no apoio = F
O valor da força F do apoio é a soma das forças verticais (para ter resultante zero), assim
F = 100 + 470 + 500 = 1070 N
[já exclui a letra D]
Para saber para que lado a gangorra vai girar ou se permanecerá em equilíbrio vamos fazer os momento de cada lado em relação ao ponto de apoio.
MA = + FA.dA = 470 x 1,5 = 705 N.m
MB = - FB.dB = - 500 x 1,6 = - 800 N.m
O Momento resultante é MRES = 705 – 800 = - 95 N.m.
Logo a gangorra pende para o lado de B (horário).
Obs.: Observe que é importante entender que a o momento de A é contrário ao momento de B. Não é preciso colocar o sinal, basta perceber que o maior momento vai fazer girar naquele sentido.
MA = FA.dA = 470 x 1,5 = 705 N.m
MB = FB.dB = 500 x 1,6 = 800 N.m
Como MB > MA a gangorra gira para B
Letra B.
10) Uma barra (20 m) de massa 200 kg é apoiada nas suas extremidades por suportes A e B. Uma pessoa começa a andar pela barra. Sabendo que a pessoa possui massa de 55 kg, determine as forças nos suportes A e B para manter a barra em equilíbrio nas seguintes situações:
(a) a pessoa está na extremidade A;
(b) a pessoa está na extremidade B;
(c) a pessoa está no centro da barra;
(d) a pessoa está a 5 m de uma das extremidades.
Solução:
a)
Perceba que neste caso, a pessoas por estar no ponto A, a reação da barra é toda no ponto A, ou seja, devido à pessoa, não há aumento de reação no ponto B.
Devido à barra, por ser supostamente homogênea (estou supondo pois o exercício não fala nada), a reação em cada ponto é igual a 100 Kg, pois ambos estão equidistantes ao centro da barra.
Neste primeiro caso então:
Reação em A: 100 + 55 = 155Kg
Reação em B: 100Kg
Verificando se o momento resultante da barre é nulo:
Momento em relação ao ponto B (poderia ser em relação ao ponto A, ou ao centro, tem que dar zero em relação a qualquer um dos pontos da barra):
55*20 (momento devido à pessoa) - 155*20 (momento devido à reação da barra no ponto A) + 200*10 (momento devido à massa da barra) = 1100 - 3100 + 2000 = 0
b) Neste caso a situação é exatamente a mesma, com a diferença que agora a reação em B passa a ser 155 Kg, e em A permanece sendo 100 Kg.
c)
Vamos agora fazer a análise para descobrir as forças:
Somatório da força resultante deve ser zero:
FA + FB - 200 - 55 = 0
Somatório dos momentos em relação a qualquer ponto deve ser zero (vou fazer em relação a B de novo):
FA*20 - 200*10 - 55*10 = 0
FA*20 = 2000 + 550
FA = 127,5 Kg
Como:
FA + FB - 200 - 55 = 0
127,5 + FB = 255
FB = 127,5 Kg
São iguais, como era de se esperar, já que todos os pesos estão concentrados no meio da barra.
d)
Da mesma forma que foi feito o anterior, devemos ter:
Força resultante igual a zero:
FA + FB - 55 - 200 = 0
FA + FB = 255
Momento resultante igual a zero (para mudar, vou fazer o momento em elação a A)
55*5 + 200*10 - FB*20 = 0
275 + 2000 = FB*20
FB*20 = 2275
FB = 113,75 Kg
Como:
FA + FB = 255
FA + 113,75 = 255
FA = 141,25 Kg






Muito obrigado ! Me ajudou bastante !
ResponderExcluirMuitooo bomm!
ResponderExcluirMuitooo bomm!
ResponderExcluirMuitooo bomm!
ResponderExcluirValeu, deu uma clareada aqui
ResponderExcluirÓtima publicação.
ResponderExcluirmuito bom, parabéns
ResponderExcluir