Leis de Kepler - resumo (com questões)

 Primeira Lei de Kepler (Lei das órbitas)

Primeira Lei de Kepler é a lei das órbitas, que diz:

“… Todos os planetas se movem em orbitas elípticas tendo o Sol como um dos focos…”  (HALLIDAY, David,  Física 2, pg. 14.)

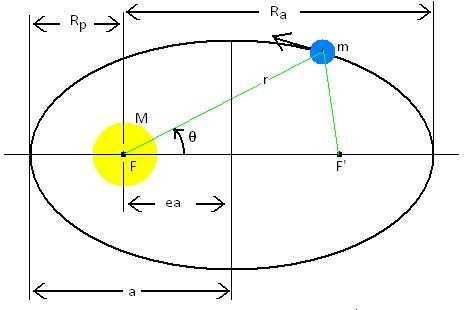
É como o caso do planeta Terra, por exemplo, que executa um movimento ao longo de uma órbita elíptica em torno doSol, embora a excentricidade seja pequena, de modo que pode ser aproximado por um círculo, dependendo do rigor da análise. Observe a figura 01, que representa uma órbita elíptica de um planeta qualquer em torno do Sol:

Note que a distância R_p representa a distância mínima do planeta ao Sol. Esta é a distância do periélio, ou seja, no caso da Terra, cuja massa é representada por m, a distância em que ela está mais próxima do Sol, cuja massa aqui é representada por M. A distância R_a representa o raio maior, ou seja, do apogeu, como exemplo do que ocorre no planeta Terra, que é a distância máxima possível de ser alcançada por estes corpos. Este tipo de movimento acontece com os corpos orbitando em torno do centro de massa. Como a massa do Sol é muito maior que a massa da Terra, o centro de massa deste sistema fica localizado dentro do próprio Sol. É a posição do foco F. O foco F’ é um ponto localizado simetricamente ao foco F, no lado oposto da elipse. Este é também conhecido como “foco vazio” (HALLIDAY, 2004).

Para a maioria dos planetas, a excentricidade e é muito pequena, e consequentemente suas órbitas são aproximadamente circulares. Note que a meia distância entre os dois focos é dada por ea, ou seja, e.a. neste caso, se a excentricidade e for zero, a distância ea também será zero, que é o caso especial do movimento circular.

O raio r, o ângulo θ e o raio maior a são úteis para a análise do movimento quando se utiliza um sistema de coordenadas polares. Neste caso, a origem do sistema de coordenadas é o corpo central, que no caso aqui citado é o Sol.

Segunda lei de Kepler (lei das áreas)

“ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas proporcionais  aos tempos gastos para percorre-las”

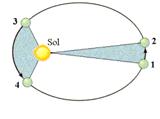
Sejam:

A₁--- área entre 1,2 e o Sol

A₂--- área entre 3, 4 e o Sol

Dt₁--- tempo que o planeta demora para ir de 1 a 2

Dt₂--- tempo que o planeta demora para ir de 3 a 4

Então:

A₁/Dt₁~A₂/Dt₂=constante=K

Essa constante K depende do planeta e recebe o nome de velocidade areolar

Observe na expressão acima que quando A₁=A₂ ®Dt₁= Dt₂, ou seja, para o arco maior 34, ser percorrido no mesmo

intervalo de tempo que o arco menor12, a velocidade em 3,4 (mais perto do Sol - periélio) deve ser maior que a velocidade em 1,2 (mais afastado do Sol – afélio).

Portanto os planetas aceleram do afélio para o periélio e retardam do periélio para o afélio. Ainda, de acordo com essa lei, se as órbitas forem circulares a velocidade de translação será constante e se a órbita do planeta tiver raio R e seu  período de translação for T, sua velocidade areolar (constante K) será dada por: K=A/Dt=pR²/T.

Terceira Lei de Kepler (Lei dos períodos)

Em uma de suas leis propostas, Johannes Kepler afirma que as órbitas descritas pelos planetas sãoelípticas. Sempre em nossos estudos consideramos que essas órbitas são circulares, portanto, se considerarmos que realmente as órbitas dos planetas são circulares, a Segunda Lei de Kepler nos diz que a velocidade do planeta é constante. Isso se dá pelo fato de a velocidade ser proporcional às áreas varridas pelo raio vetor, sendo que, na circunferência, essas áreas são iguais em intervalos de tempos iguais.

Sendo assim, esta afirmação nos permite estudar o movimento dos planetas ao redor do Sol e nos permite também estudar o movimento dos satélites ao redor dos planetas de maneira bastante aproximada. Para isso, basta fazermos uso de expressões matemáticas do movimento circular uniforme e deduzir uma nova expressão matemática para a terceira Lei de Kepler, obtendo:

Em que, na equação acima, T é o período de revolução do planeta ou o período de revolução do satélite, M é a massa do Sol e R é o raio da órbita. É interessante ressaltar que a equação acima também nos permite determinar o valor da constante k da Terceira Lei de Kepler (T² =k.R³):

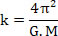
Da mesma maneira, também é possível determinar a velocidade com que o planeta descreve sua órbita, isto é, temos a possibilidade de determinar o valor da velocidade orbital de qualquer planeta ou satélite.

Para isso, basta comparar a equação que define a lei da gravitação universal com a equação da forçacentrípeta exercida sobre o planeta, ou satélite, em movimento circular uniforme. Sendo assim, teremos:

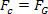
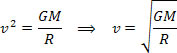
A equação acima nos fornece o módulo da velocidade orbital de um planeta ao redor do Sol. Perceba que a massa do planeta em órbita não influencia na velocidade orbital, ou seja, a velocidade orbital depende apenas do raio e da massa do Sol.

Questões resolvidas Leis de Kepler

1) Considere uma estrela em torno da qual gravita um conjunto de planetas. De acordo com a 1ª lei de Kepler:

a) Todos os planetas gravitam em órbitas circulares.

b) Todos os planetas gravitam em órbitas elípticas em cujo centro está a estrela.

c) As órbitas são elípticas, ocupando a estrela um dos focos da elipse; eventualmente, a órbita pode ser circular, ocupando a estrela o centro da circunferência.

d) A órbita dos planetas não pode ser circular.

e) A órbita dos planetas pode ter a forma de qualquer curva fechada.

2) (PUC - RJ) Um certo cometa se desloca ao redor do Sol. Levando-se em conta as Leis de Kepler, pode-se com certeza afirmar que:

a) a trajetória do cometa é uma circunferência, cujo centro o Sol ocupa;

b) num mesmo intervalo de tempo Dt, o cometa descreve a maior área, entre duas posições e o Sol, quando está mais próximo do Sol;

c) a razão entre o cubo do seu período e o cubo do raio médio da sua trajetória é uma constante;

d) o cometa, por ter uma massa bem menor do que a do Sol, não á atraído pelo mesmo;

e) o raio vetor que liga o cometa ao Sol varre áreas iguais em tempos iguais.

3) (CESGRANRIO) A força da atração gravitacional entre dois corpos celestes é proporcional ao inverso do quadrado da distância entre os dois corpos. Assim é que, quando a distância entre um cometa e o Sol diminui da metade, a força de atração exercida pelo Sol sobre o cometa:

a) diminui da metade;

b) é multiplicada por 2;

c) é dividida por 4;

d) é multiplicada por 4;

e) permanece constante.

4) (Direito. C.L.-97) Tendo em vista as Leis de Kepler sobre os movimento dos planetas, pode-se afirmar que:

a) a velocidade de um planeta, em sua órbita, aumenta à medida que ele se afasta do sol.

b) o período de revolução de um planeta é tanto maior quanto maior for sua distância do sol.

c) o período de revolução de um planeta é tanto menor quanto maior for sua massa.

d) o período de rotação de um planeta, em torno de seu eixo, é tanto maior quanto maior for seu o período de revolução.

e) o sol se encontra situado exatamente no centro da órbita elíptica descrita por um dado planeta

5) O período de Mercúrio em torno do Sol é da ordem de 0,25 vezes do ano terrestre. O raio médio da órbita de Plutão em torno do Sol é 100 vezes maior que o raio médio da órbita de Mercúrio. Calcule o valor aproximado do período de Plutão em torno do Sol, medido em anos terrestres.

Solução:

DO ENUNCIADO:

Mercúrio: T_M = 0,25 vezes do ano terrestre
Plutão: R_P = 10² R_M

1) Escrever as duas equações: uma para Mercúrio e outra para Plutão:

T²_P = K. r_P³       (I)
T²_M = K. r_M³      (II)

2) Dividir as equações e substituir os dados.

                           T_P = 250 anos terrestres

6)  O raio médio da órbita de Marte em torno Sol é aproximadamente 4 vezes maior que o raio médio da órbita de Mercúri em torno do Sol. Assim a razão entre os períodos de revolução T₁ e T₂, de Marte e de Mercúrio, respectivamente:

SOLUÇÃO:

DO ENUNCIADO:

R_Marte = 4 R_Mercúrio

2) Escrever as duas equações: uma para Marte e outra para Mercúrio.

T²₁ = K. r³_Marte       (I)T²₂ = K. r³_Mercúrio  (II)

3) Dividir as equações e substituir os dados.

                            = 8

7) Dois satélites de um planeta têm períodos de revolução igual a 32 dias e 256 dias, respectivamente. Se o raio da órbita do primeiro satélite vale 1 unidade, então o raio da órbita do segundo será:

SOLUÇÃO:

DO ENUNCIADO:

T₁ = 32 dias = (2₅) dias
T₂ = 256 dias = (2₈) dias
R₁ =1 unidade

1) Escrever as duas equações: Uma para o satélite 1 e outra para o satélite 2.

T²₁ = K. r³₁       (I)
T²₂ = K. r³₂   (II)

2) Dividir as equações e substituir os dados

R₂ = = 2³                          R₂ = 8 unidades

8) Cite as leis de Kepler do movimento dos corpos celestes.

9) Marte tem dois satélites: Fobos, que se move em órbita circular de raio 10000 km e período  3.10⁴ s, e Deimos, que tem órbita circular de raio 24000 km. Determine o período de Deimos.

Solução:

Sabemos da Terceira Lei de Kepler que: 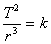, onde T é o período de translação do planeta e r é a distância média do planeta ao Sol.

Mas podemos generalizá-la para satélites que orbitam um planeta, desta forma podemos escrever: 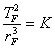, onde 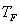 é o período orbital de Fobos em torno de Marte e 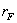 é a distância média entre

Marte e Fobos.

Também podemos escrever: , onde  é o período orbital de Deimos em torno de Marte e  é a distância média entre Marte e Deimos.

Igualando as duas equações podemos escrever: 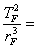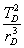, portanto temos: 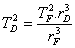, então:

 .

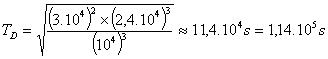10) A Terra descreve uma elipse em torno do Sol cuja área é A=6,98.10²² m². Qual é a área varrida pelo raio que liga a Terra ao Sol entre 0,0 h do dia 1º de abril até 24 h do dia 30 de abril do mesmoano.

Solução:

De acordo com a Segunda Lei de Kepler a área varrida pelo raio que liga a Terra ao Sol é proporcional ao intervalo de tempo para varrê-la. Logo se em um ano, que possui 12 meses, a área varrida é de 6,98.10²² m² ,em um mês será:.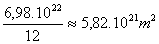

11) No sistema planetário:

a. cada planeta se move numa trajetória elíptica, tendo o sol como o centro;

b. a linha que une o sol ao planeta descreve áreas iguais em tempos iguais;

c. a razão do raio de órbita para seu período é uma constante universal;

d. a linha que liga o Sol ao planeta descreve no mesmo tempo diferentes áreas.

Alternativa: b, que descreve a Segunda Lei de Kepler.

12) ( UFCE) Dois satélites, S₁ e S₂, giram em torno da Terra em órbitas circulares de raios R₁ = 7,2 10⁷ m e R₂ =1,8 10⁷ m, respectivamente. Calcule a razão entre os períodos de S₁ e S₂, T₁/T₂ . Considere apenas a interação de cada Satélite com a Terra. 

Solução:

Dois satélites, S₁ e S₂, giram em torno da Terra em órbitas circulares de raios R₁ = 7,2 10⁷ m e R₂ =1,8 10⁷ m, respectivamente.Calcule a razão entre os períodos de S₁ e S₂, T₁/T₂ . Considere apenas a interação de cada Satélite com a Terra. 

1° - Vejamos como seria a figura descrita pelo problema. 

" Dois satélites, S₁ e S₂, giram em torno da Terra em órbitas circulares..." 

" Calcule a razão entre os períodos..." 
      A partir da expressão acima será possível determinar a razão; 

13) - (ITA ) Comentando as leis de Kepler para o movimento planetário, um estudante escreveu: 

I) Os planetas do Sistema Solar descrevem elipses em torno do Sol, que ocupa o centro dessas elipses.
II) Como o dia (do nascer ao por-do-sol) é mais curto no inverno e mais longo no verão, conclui-se que o vetor posição da Terra (linha que une esta ao Sol) varre uma área do espaço menor no inverno do que no verão, para o mesmo período de 24 h.
III) Como a distância média da Terra ao Sol é de 1,5.10⁸ km e a de Urano ao Sol é de 3.10⁹ km, pela terceira lei de Kepler conclui-se que o "ano" de Urano é igual a vinte vezes o ano da Terra.
IV) As leis de Kepler não fazem referência à força de interação entre o Sol e os planetas.
Verifique quais as afirmações que estão corretas e indique a opção correspondente:

A)I e IV estão corretas.
B) Só e I está correta.
C) II e IV estão corretas:
D) Só a IV está correte.
E) II e III estão corretas. 

Solução:

 Para entender melhor o problema, vamos ressaltar os pontos importantes da questão. Sem a compreensão deles, ficará difícil prosseguirmos ! 

      Comentando as leis de Kepler para o movimento planetário, um estudante escreveu:

I) Os planetas do Sistema Solar descrevem elipses em torno do Sol, que ocupa o centro dessas elipses.
   1ª Os Planetas descrevem órbitas elípticas em torno do Sol que ocupa um dos focos da elipse descrita.


II) Como o dia (do nascer ao por-do-sol) é mais curto no inverno e mais longo no verão, conclui-se que o vetor posição da Terra (linha que une esta ao Sol) varre uma área do espaço menor no inverno do que no verão, para o mesmo período de 24 h.



      Se o tempo (período de 24h) for o mesmo, pela lei de Kepler as áreas serão iguais.

III) Como a distância média da Terra ao Sol é de 1,5.10⁸ km e a de Urano ao Sol é de 3.10⁹ km, pela terceira lei de Kepler conclui-se que o "ano" de Urano é igual a vinte vezes o ano da Terra.



IV) As leis de Kepler não fazem referência à força de interação entre o Sol e os planetas.

      Esta é a alternativa correta. O estudo da interação entre os Corpos celestes, será feita por Newton na Gravitação Universal. 

Gabarito:

1) C    2) E     3) D    

4) Para responder esta questão primeiramente temos que saber o que é um período de revolução.

Segundo a terceira Lei de Kepler.

A razão dos quadrados dos períodos de revolução (tempo que o planeta demora a descrever uma órbita) para dois planetas é igual à razão dos cubos dos seus semieixos maiores.

Segundo estas palavras podemos apontar a letra b como resposta.

5) TP = 250 anos terrestres

6) T1/T2 = 8

7) R2 = 8 unidades

8) I – Os planetas descrevem órbitas elípticas e o Sol ocupa um dos focos.

II – A linha imaginária que liga o centro do Sol ao centro de um planeta percorre em tempos iguais áreas iguais.

III – O quadrado do período orbital de um planeta é proporcional ao cubo de sua distância média  ao Sol.

9) 1,14 . 10^5  

10) 5,82 . 10^21 m²

11) Alternativa: b, que descreve a Segunda Lei de Kepler.

12) T1/T2 = 8

13) D

Fonte: http://www.fisicaevestibular.com.br/

          http://www.alunosonline.com.br/

          http://www.infoescola.com/

          http://www.cefetsp.br/

          http://www.if.ufrgs.br/