Grandezas escalares e vetoriais
Algumas grandezas físicas exigem, para sua perfeita caracterização, apenas uma intensidade.
 Essas grandezas são denominadas grandezas escalares. Assim, grandezas físicas, como massa, comprimento, tempo, temperatura, densidade e muitas outras, são classificadas como grandezas escalares.
Essas grandezas são denominadas grandezas escalares. Assim, grandezas físicas, como massa, comprimento, tempo, temperatura, densidade e muitas outras, são classificadas como grandezas escalares.
 Por outro lado, existem grandezas físicas que, para sua perfeita caracterização, exigem, além da intensidade, uma orientação espacial (direção e sentido).
Por outro lado, existem grandezas físicas que, para sua perfeita caracterização, exigem, além da intensidade, uma orientação espacial (direção e sentido).
 Tais grandezas recebem o nome de grandezas vetoriais. Como exemplo de grandezas vetoriais, podemos citar: força, impulso, quantidade de movimento, velocidade, aceleração e muitas outras.
Tais grandezas recebem o nome de grandezas vetoriais. Como exemplo de grandezas vetoriais, podemos citar: força, impulso, quantidade de movimento, velocidade, aceleração e muitas outras.
Vetores
As grandezas vetoriais são representadas por um ente matemático denominado vetor.
Um vetor reúne, em si, o módulo, representando o valor numérico ou intensidade da grandeza, e a direção e sentido, representando a orientação da grandeza.
É importante salientarmos as diferenças entre direção e sentido: um conjunto de retas paralelas tem a mesma direção.
 e, a cada direção, podemos associar uma orientação.
e, a cada direção, podemos associar uma orientação.
A figura abaixo representa uma grandeza vetorial qualquer: um segmento de reta orientado (direção e sentido) com uma determinada medida (módulo).

![]()
 Para indicar um vetor, podemos usar qualquer uma das formas indicadas abaixo:
Para indicar um vetor, podemos usar qualquer uma das formas indicadas abaixo:
 Para indicarmos o módulo de um vetor, podemos usar qualquer uma das seguintes notações:
Para indicarmos o módulo de um vetor, podemos usar qualquer uma das seguintes notações:


 Assim,
Assim,  indica o vetor
indica o vetor  e a indica o módulo do vetor
e a indica o módulo do vetor .
.
Vetor Oposto
O vetor oposto é aquele que possui o mesmo módulo, a mesma direção e o sentido oposto. Veja a seguir um exemplo com o vetor e o seu respectivo oposto.
VETOR UNITÁRIO (VERSOR)
Chamaremos de VERSOR ou VETOR UNITÁRIO , ao vetor cujo módulo seja igual à unidade, ou seja:
| u | = u = 1.
O VETOR NULO
Vetor de módulo igual a zero, de direção e sentido indeterminados.
Notação: 0
Decomposição de vetores no plano
Quando nos referimos a grandezas escalares não temos a necessidade de fazer uso de uma palavra específica para expressar sua medida, basta expressar a própria medida, como, por exemplo: a massa de um corpo é 2 kg, o comprimento da pista é 5 km etc. Mas quando estamos trabalhando com grandezas vetoriais esse procedimento deixa de ser correto, pois a expressão da medida só dá uma parcela da informação, por exemplo: dizer que a força aplicada a um corpo é 4 N não indica a direção e o sentido da força.
Por esse motivo, em grandezas vetoriais, o correto é dizer: o módulo da força aplicada a um corpo é 4 N. Em outras situações que abordam grandezas vetoriais, temos que realizar a soma ou a subtração de vetores na mesma direção. Um caso bem interessante e que merece bastante atenção é a soma de grandezas vetoriais com vetores dispostos perpendicularmente entre si.
Quando você se deparar com uma situação onde há a necessidade de realizar a soma ou a subtração de vetores perpendiculares entre si, o melhor que você deve fazer é trabalhar com a decomposição de vetores.
Na soma de dois vetores, podemos encontrar apenas um único vetor, ou seja, o vetor resultante, que nada mais é do que um vetor que equivale a esses dois vetores. Na decomposição de vetores, o processo é inverso. Dado um vetor 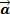 , podemos encontrar outros dois vetores
, podemos encontrar outros dois vetores 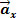 e
e 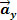 tal que
tal que 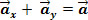 . Vejamos a figura abaixo:
. Vejamos a figura abaixo:
Nesse caso, como 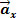 e
e .jpg) são vetores perpendiculares entre si, a decomposição é ortogonal. Veja a figura abaixo:
são vetores perpendiculares entre si, a decomposição é ortogonal. Veja a figura abaixo:
Na figura acima podemos deslocar o vetor .jpg) para a extremidade do vetor
para a extremidade do vetor 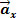 de modo que o vetor
de modo que o vetor 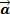 e seus vetores componentes ortogonais
e seus vetores componentes ortogonais 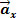 e
e .jpg) formem um triângulo retângulo.
formem um triângulo retângulo.
Com base na relação trigonométrica aplicada a um triângulo retângulo, podemos determinar o módulo dos componentes horizontal e vertical do vetor 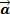 em função do ângulo θ. Dessa forma, do triângulo amarelo acima temos:
em função do ângulo θ. Dessa forma, do triângulo amarelo acima temos:
A expressão do módulo do componente horizontal
A expressão do módulo do componente vertical
Finalmente, como o triângulo formado por 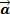 e seus componentes é um triângulo retângulo, aplicando o teorema de Pitágoras, temos:
e seus componentes é um triângulo retângulo, aplicando o teorema de Pitágoras, temos:
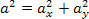
que é a relação entre o módulo do vetor e o módulo de seus componentes ortogonais.
Operações com vetores
Adição de vetores
Na adição de vetores, cada par de vetores u e v corresponderá um vetor u+v que é a soma dos vetores u e v. para adicionar dois vetores pegaremos um representante qualquer (A,B) desse vetor u e do vetor v que tem origem em B e extremidade em C. Dessa forma teremos determinada um segmento orientado (AC), que por definição representa o vetor u+v que é a soma dos vetores u e v.
- Da imagem acima concluímos que determinar o vetor u+v proveniente da soma do vetor u com o vetor v, precisamos apenas completar o triangulo, lembrando sempre de pôr a origem do vetor soma na origem do primeiro vetor, o segundo vetor deve ter a origem na extremidade do primeiro vetor.
Na adição de vetores podemos utilizar de outra ferramenta, a regra do paralelogramo. Pegamos os representantes de u e v com a mesma origem A e construímos o paralelogramo ABCD. O vetor u+v é representado pelo seguimento orientado (A,D).
Propriedades
1) Propriedade Associativa
(u+v)+w = u+(v+w) (para qualquer u,v,w pertencentes a v³)
2) Propriedade Comutativa
u+v = v+u (para qualquer u,v pertencentes a v³)
3) Elemento Neutro
u+0 = u (para qualquer u pertencentes a v³)
4) Elemento Oposto
Para um dado vetor u qualquer, existe um vetor que quando somado a ele dará como resultado um vetor nulo. Este vetor é o vetor oposto a u, denominado de –u
u+(-u) = AB +AB = AA = 0
Observe que a subtração de vetores é simplesmente a soma de um vetor com um vetor oposto. Exemplo:
u-v = u+(-v) (para qualquer u,v pertencentes a v³)
Adição vetorial gráfica
A primeira maneira de se somar dois ou mais vetores é a forma gráfica. A regra é simples: cada vetor a ser somado é colocado de maneira que o final de um coincida com o início do próximo. O vetor resultante será obtido unindo-se o início do primeiro com o final do último.
Note no exemplo acima que o vetor  une o início do vetor
une o início do vetor  ao final do vetor
ao final do vetor 
Veja este outro exemplo:
Note que a resultante  é a soma dos vetores ou
é a soma dos vetores ou 
Adição vetorial por decomposição
Veja agora este exemplo:
Calcule que a soma do vetor  com o
com o  , sabendo-se que o módulo de
, sabendo-se que o módulo de  e
e  , e que os ângulos com a horizontal são respectivamente 60° e 30°.
, e que os ângulos com a horizontal são respectivamente 60° e 30°.
Primeiro se decompõe o vetor  em dois vetores um vertical e outro horizontal.
em dois vetores um vertical e outro horizontal.
Onde:
Como a é 60° tem-se:
O mesmo se dá para o vetor 
Agora é só somar os componentes verticais e horizontais que são respectivamente 22,3 e 18,7. O vetor resultante terá o módulo:
E um ângulo com a horizontal b igual:
Regra do Polígono |  |
 Para efetuarmos a adição de vetores pela regra do polígono, escolhemos, arbitrariamente, um dos vetores como ponto de partida e traçamos os vetores seguintes, colocando a origem do 2º vetor coincidindo com a extremidade do 1º e, assim, sucessivamente, até traçarmos todos os vetores. O vetor soma
Para efetuarmos a adição de vetores pela regra do polígono, escolhemos, arbitrariamente, um dos vetores como ponto de partida e traçamos os vetores seguintes, colocando a origem do 2º vetor coincidindo com a extremidade do 1º e, assim, sucessivamente, até traçarmos todos os vetores. O vetor soma  ou resultante
ou resultante  é determinado pela origem do 1º vetor e pela extremidade do último vetor traçado.
é determinado pela origem do 1º vetor e pela extremidade do último vetor traçado.
Exemplo:
Obter, pelo método do polígono, a resultante das forças F1 = F2 = 100 N
Resolução
 Construindo o polígono, obtemos um triângulo equilátero portanto o resultante tem intensidade igual à das forças componentes.
Construindo o polígono, obtemos um triângulo equilátero portanto o resultante tem intensidade igual à das forças componentes.
Subtração de Vetores
Produto escalar
Dados os vetores u=(a,b) e v=(c,d) definimos o produto escalar entre os vetores u e v, como o número real obtido por:
u.v = a.c + b.d
Exemplos:
O produto escalar entre u=(3,4) e v=(-2,5) é:
u.v = 3.(-2) + 4.(5) = -6+20 = 14
O produto escalar entre u=(1,7) e v=(2,-3) é:
u.v = 1.(2) + 7.(-3) = 2-21 = -19
Propriedades do produto escalar
Quaisquer que sejam os vetores, u v e w e k escalar:
|
|
Método das Componentes Vetoriais
 |  |
 Todo vetor
Todo vetor  , em um plano, pode ser representado por dois outros vetores, chamados de componentes retangulares.
, em um plano, pode ser representado por dois outros vetores, chamados de componentes retangulares.
 Dado um vetor
Dado um vetor  e duas direções de referência OX e OY, determinamos as componentes retangulares do vetor
e duas direções de referência OX e OY, determinamos as componentes retangulares do vetor  através das projeções perpendiculares da origem e da extremidade do vetor nas direções dadas, conforme figura a seguir.
através das projeções perpendiculares da origem e da extremidade do vetor nas direções dadas, conforme figura a seguir.
 O vetor
O vetor  pode ser representado pelas suas componentes retangulares
pode ser representado pelas suas componentes retangulares  x e
x e  y, sendo válida a relação
y, sendo válida a relação
Para determinarmos os módulos das componentes  x e
x e y, devemos usar as relações trigonométricas no triângulo retângulo.
y, devemos usar as relações trigonométricas no triângulo retângulo.


Vetor Posição |  |

 Consideremos um corpo descrevendo uma trajetória curva em relação a um sistema de coordenadas retangulares xy, conforme a figura. Consideremos um corpo descrevendo uma trajetória curva em relação a um sistema de coordenadas retangulares xy, conforme a figura.

A posição P do corpo, num instante t qualquer, pode ser fornecida pelas coordenadas x e y e o movimento do corpo pode ser descrito pelas funções horárias.

x = f(t) e y = f(t)

Podemos também fornecer a posição do corpo pelo vetor  , um vetor com origem no ponto 0 (referencial) e extremidade no ponto P. Esse vetor r recebe o nome de vetor posição. , um vetor com origem no ponto 0 (referencial) e extremidade no ponto P. Esse vetor r recebe o nome de vetor posição.

Quando um corpo se movimenta numa trajetória curva qualquer, o vetor posição  varia no decorrer do tempo. Essa variação no vetor posição ocorre, obrigatoriamente, na direção e no sentido, mas não obrigatoriamente no módulo. varia no decorrer do tempo. Essa variação no vetor posição ocorre, obrigatoriamente, na direção e no sentido, mas não obrigatoriamente no módulo. |  |  |  |

Se o móvel se movimenta do ponto P1 para o ponto P2, dizemos que ele sofreu um deslocamento vetorial  dado por dado por

O vetor  , que representa o deslocamento vetorial do móvel entre os instantes t1 e t2, é um vetor com origem em P1 (posição inicial) e extremidade em P2 (posição final). , que representa o deslocamento vetorial do móvel entre os instantes t1 e t2, é um vetor com origem em P1 (posição inicial) e extremidade em P2 (posição final).

O módulo do vetor deslocamento  é dado por: é dado por:
 | 
Velocidade Vetorial Média
 |  |

O vetor velocidade vetorial média  é definido pela relação entre o vetor deslocamento é definido pela relação entre o vetor deslocamento  e o correspondente intervalo de tempo e o correspondente intervalo de tempo 

Como o intervalo de tempo  é sempre positivo, o vetor velocidade vetorial média possui a mesma direção e o mesmo sentido que o vetor deslocamento é sempre positivo, o vetor velocidade vetorial média possui a mesma direção e o mesmo sentido que o vetor deslocamento  . . |
|
|
|
|
|
|
|
|
ACELERAÇÃO VETORIAL INSTANTÂNEA
É a aceleração vetorial de um móvel em cada ponto de sua trajetória.
Como todo vetor pode ser obtido pela soma de suas componentes perpendiculares, vamos decompor o vetor aceleração instantânea, tomando como base a direção do vetor velocidade:
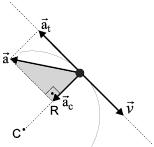
a) Aceleração tangencial (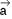 t) – É a componente da aceleração vetorial na direção do vetor velocidade ( ) e indica a variação do módulo deste. Possui módulo
t) – É a componente da aceleração vetorial na direção do vetor velocidade ( ) e indica a variação do módulo deste. Possui módulo
igual ao da aceleração escalar:
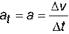
Importante:
1) Em movimentos acelerados, 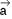 t e
t e 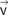 têm o mesmo sentido.
têm o mesmo sentido.
2) Em movimentos retardados,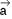 t e
t e 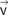 têm sentidos contrários, como na figura anterior.
têm sentidos contrários, como na figura anterior.
3) Em movimentos uniformes,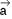 t é nula, já que o módulo de
t é nula, já que o módulo de 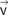 não varia nesses movimentos.
não varia nesses movimentos.
b) Aceleração centrípeta ou normal (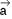 c) – É a componente da aceleração vetorial na direção do raio de curvatura (R) e indica a variação da direção do vetor velocidade (
c) – É a componente da aceleração vetorial na direção do raio de curvatura (R) e indica a variação da direção do vetor velocidade (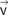 ). Tem sentido apontando para o centro da trajetória (por isso, centrípeta) e módulo
). Tem sentido apontando para o centro da trajetória (por isso, centrípeta) e módulo
dado por:
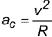
Importante: nos movimentos retilíneos,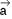 c é nula porque o móvel não muda de direção nesses movimentos.
c é nula porque o móvel não muda de direção nesses movimentos.
Aceleração vetorial resultante – A obtenção da intensidade da aceleração resultante pode ser feita aplicando-se o Teorema de Pitágoras no triângulo retângulo em destaque na figura:
a2 = a2t + a2c
Exemplo:
01. (PUC–SP) Um móvel parte do repouso e percorre uma trajetória circular de raio 100m, em movimento acelerado
uniformemente, de aceleração escalar igual 1m/s2. Calcule, após 10s, as componentes tangencial e centrípeta da aceleração.
Solução:
 .
.
Módulo de um vetor
O módulo ou comprimento do vetor v=(a,b) é um número real não negativo, definido por:
Vetor unitário
Vetor unitário é o que tem o módulo igual a 1.
Existem dois vetores unitários que formam a base canônica para o espaço R², que são dados por:
i = (1,0) j = (0,1)
Para construir um vetor unitário u que tenha a mesma direção e sentido que um outro vetor v, basta dividir o vetor v pelo seu módulo, isto é:
Observação:
Para construir um vetor u paralelo a um vetor v, basta tomar u=cv, onde c é um escalar não nulo. Nesse caso, u e v serão paralelos:
Se c = 0, então u será o vetor nulo.
Se 0 < c < 1, então u terá comprimento menor do que v.
Se c > 1, então u terá comprimento maior do que v.
Se c < 0, então u terá sentido oposto ao de v.
Decomposição de vetores em Vetores Unitários
Para fazer cálculos de vetores em apenas um dos planos em que ele se apresenta, pode-se decompor este vetor em vetores unitários em cada um dos planos apresentados.
Sendo simbolizados, por convenção, î como vetor unitário do plano x e 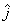 como vetor unitário do plano y. Caso o problema a ser resolvido seja dado em três dimensões, o vetor utilizado para o plano z é o vetor unitário
como vetor unitário do plano y. Caso o problema a ser resolvido seja dado em três dimensões, o vetor utilizado para o plano z é o vetor unitário 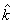 .
.
Então, a projeção do vetor 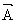 no eixo x do plano cartesiano será dado por
no eixo x do plano cartesiano será dado por 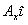 , e sua projeção no eixo ydo plano será:
, e sua projeção no eixo ydo plano será: 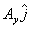 . Este vetor pode ser escrito como:
. Este vetor pode ser escrito como:
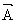 =(
=(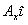 ,
,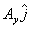 ), respeitando que sempre o primeiro componente entre parênteses é a projeção em x e o segundo é a projeção no eixo y. Caso apareça um terceiro componente, será o componente do eixo z.
), respeitando que sempre o primeiro componente entre parênteses é a projeção em x e o segundo é a projeção no eixo y. Caso apareça um terceiro componente, será o componente do eixo z.
No caso onde o vetor não se encontra na origem, é possível redesenhá-lo, para que esteja na origem, ou então descontar a parte do plano onde o vetor não é projetado.
Ângulo entre dois vetores
O produto escalar entre os vetores u e v pode ser escrito na forma:
u.v = |u| |v| cos(x)
onde x é o ângulo formado entre u e v.
Através desta última definição de produto escalar, podemos obter o ângulo x entre dois vetores genéricos u e v, como,
desde que nenhum deles seja nulo.
Questões resolvidas sobre vetores
1) (UFAL) Considere as grandezas físicas:
I. Velocidade
II. Temperatura
III. Quantidade de movimento
IV. Deslocamento
V. Força
Destas, a grandeza escalar é:
a) I
b) II
c) III
d) IV
e) V
2) (CESGRANRIO) Das grandezas citadas nas opções a seguir assinale aquela que é de natureza vetorial:
a) pressão
b) força eletromotriz
c) corrente elétrica
d) campo elétrico
e) trabalho
3) (UEPG - PR) Quando dizemos que a velocidade de uma bola é de 20 m/s, horizontal e para a direita, estamos definindo a velocidade como uma grandeza:
a) escalar
b) algébrica
c) linear
d) vetorial
e) n.d.a.
4) (FESP) Num corpo estão aplicadas apenas duas forças de intensidades 12N e 8,0N. Uma possível intensidade da resultante será:
a) 22N
b) 3,0N
c) 10N
d) zero
e) 21N
Solução:
2 FORÇAS APLICADAS EM 12N E 8N, LOGO:
N+N=12+8
2N=20
N=20/2
N=10N
5) Suponha que uma partícula se move com aceleração escalar de 3 m/s2 em uma trajetória circular cujo raio é igual a 24 m. No instante t = 0, a velocidade dessa partícula é igual a 6 m/s. Assim, determine o módulo da aceleração tangencial e marque a alternativa correta.
a) 2 m/s2
b) 3m/s2
c) 4 m/s2
d) 5 m/s2
e) 6 m/s2
Solução:
Em uma trajetória curva, a aceleração tangencial possui o mesmo módulo, ou seja, o mesmo valor da aceleração escalar, portanto o valor da aceleração tangencial é 3 m/s2.
6) Suponha que você tenha uma partícula em movimento circular uniforme. Podemos dizer que:
a) aceleração vetorial é constante
b) o módulo da velocidade vetorial é constante
c) o módulo da aceleração vetorial é nulo
d) a velocidade vetorial é constante
e) a velocidade vetorial tem seu sentido para o centro da trajetória
7) Em que movimentos permanece constante:
a) o módulo da velocidade vetorial;
b) a direção de velocidade vetorial;
c) a velocidade vetorial.
8) (UFPA) Uma partícula percorre, com movimento uniforme, uma trajetória não retilínea. Em cada instante teremos que:
a) Os vetores velocidade e aceleração são paralelos entre si;
b) A velocidade vetorial é nula;
c) Os vetores velocidade e aceleração são perpendiculares entre si;
d) Os vetores velocidade a aceleração têm direções independentes;
e) O valor do ângulo entre o vetor velocidade e o vetor aceleração muda de ponto a ponto.
9) (MACKENZIE) Um corpo é atirado verticalmente para cima a partir do solo com velocidade inicial de módulo 50 m/s. O módulo de sua velocidade vetorial média entre o instante de lançamento e o instante em que retorna ao solo é:
a) 50 m/s
b) 25 m/s
c) 5,0 m/s
d) 2,5 m/s
e) zero
10) Considere uma partícula em movimento.
A respeito de sua velocidade vetorial (instantânea) assinale a opção falsa:
a) tem direção sempre tangente à trajetória;
b) tem sentido sempre concordante com o sentido do movimento;
c) tem intensidade sempre igual ao valor absoluto da velocidade escalar (instantânea);
d) somente é constante se o movimento for retilíneo e uniforme;
e) é constante no movimento circular e uniforme.
11) Um veiculo faz uma curva de 100 m de raio com velocidade constante de 72 Km/h. Calcule a aceleração tangencial e vetorial.
Solução:
V= d/t V= 72km/h = 20m/s
20 = 100/t
20t = 100
t = 100/20
t =5s
V =a .t
20 = a.5
a = 20/5
a= 4m/s²
12) Um veiculo com aceleração tangencial de 8m/s² faz uma curva de raio 150 m. Num certo instante a velocidade desse veiculo é de 108 Km/h. Calcule para esse instante a aceleração vetorial.
Solução:
V = 108km/h = 30m/s
d = a.t²/2
150 = 8.t²/2
300 = 8t²
300/8 = t²
t² = 37,5
t = 6s
30 = a.6
a = 30/6
a= 5m/s²
13) Dados os vetores no plano R2 , u = 2 i - 5 j e v = i + j , pede-se determinar:
a) o vetor soma u + v
b) o módulo do vetor u + v
c) o vetor diferença u - vd) o vetor 3 u - 2 ve) o produto interno u.v
SOLUÇÃO:
a) Temos: u = (2, -5) e v = (1, 1). Logo, u + v = (2, -5) + (1, 1) = (3, -4) = 3 i - 4 jb) | u + v| = Ö 32 + 42 = Ö 25 = 5 ou 5 u.c (u.c. = unidades de comprimento).
c) u - v = (2, -5) - (1, 1) = (1, -6) = i - 6 jd) 3u - 2v = 3.(2, -5) -2( 1, 1) = (6, -15) + (-2, -2) = (4, -17) = 4 i - 17 je) u.v = 2.1 + (-5).1 = - 3
14) Um projétil é lançado com uma velocidade de módulo 20 m/s e formando com o plano horizontal um ângulo de 60°. Calcule os componentes horizontal e vertical da velocidade.
Solução:
Vx = 10m/s
15) Um corpo é atirado verticalmente para cima a partir do solo com velocidade inicial de módulo 50 m/s. O módulo de sua velocidade vetorial média entre o instante de lançamento e o instante em que retorna ao solo é:
a) 50 m/s
b) 25 m/s
c) 5,0 m/s
d) 2,5 m/s
e) zero
Gabarito:
1) B 2) D 3) D 4) C 5) B 6) B
7) a) O módulo da velocidade vetorial é igual ao da velocidade escalar e será constante se o movimento for uniforme.
b) A velocidade vetorial terá direção constante se a trajetória for retilínea.
c) Para a velocidade vetorial ser constante ela deve ser todas as suas características constantes e, portanto, o movimento deverá ser retilíneo e uniforme.
8) C
9) E
10) E
15) E



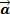 , podemos encontrar outros dois vetores
, podemos encontrar outros dois vetores 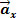 e
e 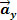 tal que
tal que 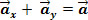 . Vejamos a figura abaixo:
. Vejamos a figura abaixo: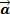 , podemos encontrar outros dois vetores
, podemos encontrar outros dois vetores 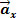 e
e 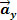 tal que
tal que 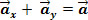 . Vejamos a figura abaixo:
. Vejamos a figura abaixo: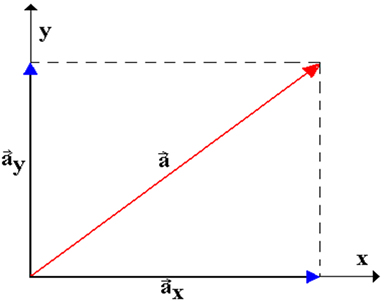
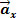 e
e .jpg) são vetores perpendiculares entre si, a decomposição é ortogonal. Veja a figura abaixo:
são vetores perpendiculares entre si, a decomposição é ortogonal. Veja a figura abaixo: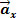 e
e .jpg) são vetores perpendiculares entre si, a decomposição é ortogonal. Veja a figura abaixo:
são vetores perpendiculares entre si, a decomposição é ortogonal. Veja a figura abaixo: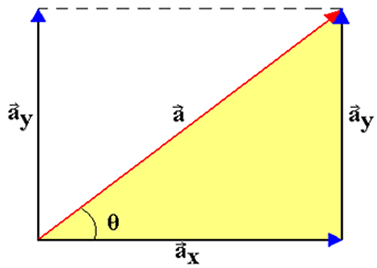
.jpg) para a extremidade do vetor
para a extremidade do vetor 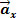 de modo que o vetor
de modo que o vetor 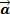 e seus vetores componentes ortogonais
e seus vetores componentes ortogonais 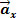 e
e .jpg) formem um triângulo retângulo.
formem um triângulo retângulo..jpg) para a extremidade do vetor
para a extremidade do vetor 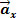 de modo que o vetor
de modo que o vetor 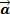 e seus vetores componentes ortogonais
e seus vetores componentes ortogonais 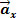 e
e .jpg) formem um triângulo retângulo.
formem um triângulo retângulo.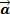 em função do ângulo θ. Dessa forma, do triângulo amarelo acima temos:
em função do ângulo θ. Dessa forma, do triângulo amarelo acima temos: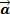 em função do ângulo θ. Dessa forma, do triângulo amarelo acima temos:
em função do ângulo θ. Dessa forma, do triângulo amarelo acima temos: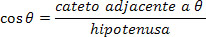
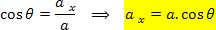
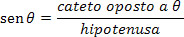
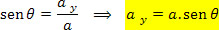
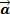 e seus componentes é um triângulo retângulo, aplicando o teorema de Pitágoras, temos:
e seus componentes é um triângulo retângulo, aplicando o teorema de Pitágoras, temos: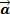 e seus componentes é um triângulo retângulo, aplicando o teorema de Pitágoras, temos:
e seus componentes é um triângulo retângulo, aplicando o teorema de Pitágoras, temos: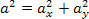
 une o início do vetor
une o início do vetor  ao final do vetor
ao final do vetor 
 une o início do vetor
une o início do vetor  ao final do vetor
ao final do vetor 

 é a soma dos vetores ou
é a soma dos vetores ou 
 é a soma dos vetores ou
é a soma dos vetores ou 

 com o
com o  , sabendo-se que o módulo de
, sabendo-se que o módulo de  e
e  , e que os ângulos com a horizontal são respectivamente 60° e 30°.
, e que os ângulos com a horizontal são respectivamente 60° e 30°. com o
com o  , sabendo-se que o módulo de
, sabendo-se que o módulo de  e
e  , e que os ângulos com a horizontal são respectivamente 60° e 30°.
, e que os ângulos com a horizontal são respectivamente 60° e 30°. em dois vetores um vertical e outro horizontal.
em dois vetores um vertical e outro horizontal. em dois vetores um vertical e outro horizontal.
em dois vetores um vertical e outro horizontal.












 x e
x e y, devemos usar as relações trigonométricas no triângulo retângulo.
y, devemos usar as relações trigonométricas no triângulo retângulo.













 .
.
Nenhum comentário:
Postar um comentário