Solução:
Pelo enunciado temos:
2sen(α) = 3tg²(α)
Sabendo que tg(α) = sen(α)/cos(α), substituímos e chegamos a
2sen(α) = 3sen²(α)/cos²(α)
3sen²(α) = 2sen(α)cos²(α)
3sen(α) = 2cos²(α)
Se, pela relação fundamental, sen²(α) + cos²(α) = 1, então cos²(α) = 1 - sen²(α). Então, substituindo e fazendo x = sen(α):
3sen(α) = 2 - 2sen²(α)
3x = 2 - 2x²
2x² + 3x - 2 = 0
x = {-2, 1/2}
Como x = sen(α), o único valor válido é x = 1/2. Agora que sabemos o valor de sen(α), usamos esse valor na equação que achamos anteriormente:
3sen(α) = 2cos²(α)
3/2 = 2cos²(α)
cos²(α) = 3/4
cos(α) = √3/2
2) (FUVEST-SP) Os lados de um triângulo medem √5, √10 e 5. Qual o comprimento da altura relativa ao lado maior?
Solução:
Vamos fazer o desenho para representar a situação, assumindo que a altura encontra a base no ponto D e divide o lado AC em duas partes: a e 5 - a.
Aplicando a lei dos cossenos no triângulo ABC, referente ao ângulo α:
(√10)² = (√5)² + 5² - 2 * √5 * 5 * cos(α)
10 = 30 - 10√5 * cos(α)
cos(α) = 2√5/5
No triângulo ABD:
cos(α) = a/√5 = 2√5/5
5a = 10
a = 2
Ainda em ABD, aplicando Pitágoras:
h² + 2² = (√5)² => h = 1
Uma resolução mais curta e direta é montar um sistema de equações aplicando Pitágoras nos dois triângulos retângulos e resolvê-lo. Fica aí a sugestão, caso queira complementar.
3)

Uma folha quadrada de papel ABCD é dobrada de modo que o vértice C coincide com o ponto M, médio de AB. SE o lado de ABCD é 1, o comprimento BP é:
a) 0,300.
b) 0,325.
c) 0,375.
d) 0,450.
e) 0,500.
Sabemos que MB vale 1/2 e o ângulo CBP é reto, mas não dá para fazer muita coisa só com essas informações, não é mesmo? Pois bem, façamos o seguinte para descobrir PC. Na folha original, antes de ser dobrada, notamos que o lado CB vale 1. Assim sendo, se BP vale 1, então PC vale 1 - x:

Ora, o comprimento de PC não muda quando dobramos o papel, então ficamos com a figura abaixo:
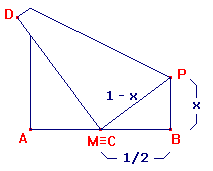
Aplicando Pitágoras, temos
x² + (1/2)² = (1 - x)²
x = 0,75/2 = 0,375
Alternativa c.
4) Um avião decola, percorrendo uma trajetória retilínea, formando com o solo, um ângulo de 30º (suponha que a região sobrevoada pelo avião seja plana). Depois de percorrer 1 000 metros, qual a altura atingida pelo avião?
Solução:
.gif)
A altura será de 500 metros
5) (USININOS-RS) Um avião levanta voo sob um ângulo constante de 20º. Após percorrer 2 000 metros em linha reta, qual será a altura atingida pelo avião, aproximadamente? (Utilize: sem 20º = 0,342; cos 20º = 0,94 e tg 20º = 0,364)
Solução:
.gif)
.gif)
A altura atingida pelo avião será de 684 metros.


7) Determine o valor do lado oposto ao ângulo de 60º. Observe figura a seguir:
.jpg)
x² = 6² + 8² - 2 * 6 * 8 * cos 60º
x² = 36 + 64 – 96 * 1/2
x² = 100 – 48
x² = 52
√x² = √52
x = 2√3
.jpg)
x² = 6² + 8² - 2 * 6 * 8 * cos 60º
x² = 36 + 64 – 96 * 1/2
x² = 100 – 48
x² = 52
√x² = √52
x = 2√3
8) O menor arco positivo "x", para o qual
é:
(A) 
(B) 
(C) 
(D) 
(E) 
Solução:
Aplicando as propriedades de potenciação e igualando as bases, temos:
Cortando as bases:
O menor arco que possui cosseno igual a 1/2 é 60o,ou seja,  resposta certa, letra “C”
resposta certa, letra “C”
9) Se sen  e α for pertencente ao 4º Quadrante, o valor da expressão
e α for pertencente ao 4º Quadrante, o valor da expressão  será:
será:
(A) 28
(B) -24
(C) -26
(D) 27
(E) 25
(B) -24
(C) -26
(D) 27
(E) 25
Solução:
Utilizando a equivalência fundamental da trigonometria, sen²(x) + cos²(x) = 1
Podemos calcular o valor de cos α:

Sabendo que α está no quarto quadrante, então o co-seno é positivo e vale 3/5.
Sabendo que temos que tan α = - 4/3
temos que tan α = - 4/3
Agora iremos utilizar as seguintes fórmulas:
podemos fazer uma transformação nestas fórmulas e utilzá-las da seguinte maneira:
 (1)
(1)
 (2)
(2)
estas transformações são válidas, pois a fórmula diz que o seno do dobro de um arco é igual à duas vezes o seno deste arco vezes o co-seno deste arco. Vamos tomar nosso arco como sendo x/2, portanto o dobro deste arco será x. O mesmo vale para o co-seno.
Na equação (2) vamos isolar o valor de e substituir o valor de cos x que já sabemos:
e substituir o valor de cos x que já sabemos:

Veja que a raiz trouxe duas opçoes, ou + ou –, qual iremos utilizar? Como o ângulo é do quarto quadrante, a metade deste ângulo será do segundo quadrante, portanto terá seno positivo, vale o +.

Para calcular melhor esta equação, vamos elevar os dois lados da equação ao quadrado. O valor de sen x já sabemos, podemos substituí-lo.
 Dá para cortar o 16 com o 4
Dá para cortar o 16 com o 4
Para facilitar os cálculos daqui para frente, vamos chamar o+=Y) , ou seja:
, ou seja:

Aplicando Bhaskara, achamos como raízes:
Como , ou seja, é um número elevado ao quadrado, não pode ter como resposta um valor negativo, portanto, o único valor que Y pode admitir é 4/5:
, ou seja, é um número elevado ao quadrado, não pode ter como resposta um valor negativo, portanto, o único valor que Y pode admitir é 4/5:

Pronto, achamos o valor de
Agora só nos falta achar o valor de , utilizaremos a fórmula:
, utilizaremos a fórmula:


Resposta correta, letra “C”

12) SENDO TETA UM ÂNGULO AGUDO E UM TRIÂNGULO RETÂNGULO QUALQUER, SABE-SE QUE O SENO DE TETA É IGUAL 0.6.
DETERMINE O COSSENO E A TANGENTE DE TETA.
Solução:
senθ =6/10 ou 3/5 (co/hip)
hip² =co²+ca²
5² =3²+ca²
ca² =25-9
ca²=16
ca = 4
cosθ =ca/hip = 4/10 ou 0,4
tgθ =co/ca ou senθ/cosθ
tgθ = 3/4 = 0,75
13) Calcular o valor de seno, cosseno e tangente do angulo alfa no triangulo retângulo cuja a hipotenusa é 4, cateto oposto é 2 e o cateto adjacente é 2 raiz de 3. Só que o angulo no triangulo é reto em cima.
Sabendo que:
- sen (x) = cateto oposto / hipotenusa
- cos (x) = cateto adjacente / hipotenusa
- tg (x) = sen (x) / cos (x)
sen (x) = 2/4 = 1/2 <=> sen^[-1] (1/2) = π/6 --> ângulo alfa
cos (x) = 2√3 / 4 = √3 / 2 <=> cos^[-1] (√3/2) = π/6 --> ângulo alfa
tg (x) = (1/2)/ √3/2 = 1/√3
Podemos calcular o valor de cos α:
Sabendo que α está no quarto quadrante, então o co-seno é positivo e vale 3/5.
Sabendo que
Agora iremos utilizar as seguintes fórmulas:
cos(2x) = cos²(x) - sen²(x)
sen(2x) = 2sen(x)cos(x)
podemos fazer uma transformação nestas fórmulas e utilzá-las da seguinte maneira:
estas transformações são válidas, pois a fórmula diz que o seno do dobro de um arco é igual à duas vezes o seno deste arco vezes o co-seno deste arco. Vamos tomar nosso arco como sendo x/2, portanto o dobro deste arco será x. O mesmo vale para o co-seno.
Na equação (2) vamos isolar o valor de
Veja que a raiz trouxe duas opçoes, ou + ou –, qual iremos utilizar? Como o ângulo é do quarto quadrante, a metade deste ângulo será do segundo quadrante, portanto terá seno positivo, vale o +.
Agora que já sabemos este valor, vamos substituí-lo na equação (1)
Para calcular melhor esta equação, vamos elevar os dois lados da equação ao quadrado. O valor de sen x já sabemos, podemos substituí-lo.
Para facilitar os cálculos daqui para frente, vamos chamar o
Aplicando Bhaskara, achamos como raízes:
Y'=4/5
Y''=-1/5
Y''=-1/5
Como
Como α/2 está no segundo quadrante, seu cosseno será negativo, portanto, vale a raiz negativa.
Pronto, achamos o valor de
Agora só nos falta achar o valor de
Pronto, já temos todas as informações pedidas, agora é só substituir na fórmula pedida.
Resposta correta, letra “C”
10) O conjunto imagem da função trigonométrica 
Solução:
Esta função é muito difícil de se determinar a imagem, no formato em que se encontra.
Devemos então "transformá-la" para que fique em um formato mais fácil de calcular o que se pede!
A transformação é a seguinte:
| Vamos começar com a principal jogada desta transformação, multiplicar a função por | |
| Agora vamos efetuar a multiplicação: | |
| Esta parte é um pouco complicada. Vamos colocar o termo | |
| Note que | |
| Agora veja, que dentro dos colchetes temos uma expressão que podemos trocar por sen(45o-x), lembrando da fórmula: sen(a-b)=sen(a)cos(b)-sen(b)cos(a) | |
| Pronto, agora é fácil calcular a imagem desta função. A imagem de sen(45o-x) é de -1 até 1, portanto, o valor máximo que f(x) poderá atingir é quando sen(45o-x) for igual a 1, portanto, o valor máximo de f(x) será A imagem de f(x) será |

12) SENDO TETA UM ÂNGULO AGUDO E UM TRIÂNGULO RETÂNGULO QUALQUER, SABE-SE QUE O SENO DE TETA É IGUAL 0.6.
DETERMINE O COSSENO E A TANGENTE DE TETA.
Solução:
senθ =6/10 ou 3/5 (co/hip)
hip² =co²+ca²
5² =3²+ca²
ca² =25-9
ca²=16
ca = 4
cosθ =ca/hip = 4/10 ou 0,4
tgθ =co/ca ou senθ/cosθ
tgθ = 3/4 = 0,75
13) Calcular o valor de seno, cosseno e tangente do angulo alfa no triangulo retângulo cuja a hipotenusa é 4, cateto oposto é 2 e o cateto adjacente é 2 raiz de 3. Só que o angulo no triangulo é reto em cima.
Sabendo que:
- sen (x) = cateto oposto / hipotenusa
- cos (x) = cateto adjacente / hipotenusa
- tg (x) = sen (x) / cos (x)
sen (x) = 2/4 = 1/2 <=> sen^[-1] (1/2) = π/6 --> ângulo alfa
cos (x) = 2√3 / 4 = √3 / 2 <=> cos^[-1] (√3/2) = π/6 --> ângulo alfa
tg (x) = (1/2)/ √3/2 = 1/√3
14) NUM TRIANGULO RETANGULO DE HIPOTENUSA 10 cm, AS MEDIDAS DOS CATETOS ESTAO NA RAZAO DE 1 PARA 3.?
Analise as afirmações a respeito dessa situação:
I. no instante t = 3 h a altura da maré é de 2 m.
II. no instante t = 6 h ocorreu a maré baixa, cuja altura é de 0,1 m.
III. no instante t = 12 h ocorre maré alta, cuja altura é de 3,9 m.
É correto o que se afirma em
(A) I, II e III.
(B) II e III, apenas.
(C) I e III, apenas.
(D) I e II, apenas.
(E) I, apenas.
Solução:
Para t= 3 h
y= 2 + 1,9 . cos(π.t/6) = 2 + 1,9 . cos(π.3/6) =2 + 1,9 . cos(π/2)
y= 2 + 1,9 . cos(90°) = 2 + 1,9 . 0 = 2 m
Para t= 6 h
y= 2 + 1,9 . cos(π.t/6) = 2 + 1,9 . cos(π.6/6) = 2 + 1,9 . cos(π)
y = 2 + 1,9 . cos(180°) = 2 + 1,9 . (-1) = 2 - 1,9 = 0,1 m
Para t= 12 h
y=2 + 1,9 . cos(π.t/6) = 2 + 1,9 . cos(π.12/6) = 2 + 1,9 . cos(2π)
y= 2 + 1,9 . cos(360°) = 2 + 1,9 . 1 = 2 + 1,9 = 3,9 m
DETERMINE AS MEDIDAS DAS PROJEÇÕES DOS CATETOS NA HIPOTENUSA.
Solução:
a =10
b/c =1/3 → c = 3b
a² =b²+c²
100 =b²+9b²
10b² =100
b =√10
c=3√10
Projeções sobre a hipotenusa:
b² = a.m
10 =10m
m=1cm
c² =a.n
90 =10n
n=9 cm
15) . (Vunesp, 2010) Em certo dia do ano, em uma cidade, a maré alta ocorreu à meia-noite. A altura da água no porto dessa cidade é uma função periódica, pois oscila regularmente entre maré alta e maré baixa, ou seja, a altura da maré aumenta até atingir um valor máximo (maré alta) e vai diminuindo até atingir um valor mínimo (maré baixa), para depois aumentar de novo até a maré alta, e assim por diante. A altura y, em metros, da maré, nesse dia, no porto da cidade, pode ser obtida, aproximadamente, pela fórmula: y=2+1,9.cos(π.t/6), sendo t o tempo decorrido, em horas, após a meia noite.
Analise as afirmações a respeito dessa situação:
I. no instante t = 3 h a altura da maré é de 2 m.
II. no instante t = 6 h ocorreu a maré baixa, cuja altura é de 0,1 m.
III. no instante t = 12 h ocorre maré alta, cuja altura é de 3,9 m.
É correto o que se afirma em
(A) I, II e III.
(B) II e III, apenas.
(C) I e III, apenas.
(D) I e II, apenas.
(E) I, apenas.
Solução:
Para t= 3 h
y= 2 + 1,9 . cos(π.t/6) = 2 + 1,9 . cos(π.3/6) =2 + 1,9 . cos(π/2)
y= 2 + 1,9 . cos(90°) = 2 + 1,9 . 0 = 2 m
Para t= 6 h
y= 2 + 1,9 . cos(π.t/6) = 2 + 1,9 . cos(π.6/6) = 2 + 1,9 . cos(π)
y = 2 + 1,9 . cos(180°) = 2 + 1,9 . (-1) = 2 - 1,9 = 0,1 m
Para t= 12 h
y=2 + 1,9 . cos(π.t/6) = 2 + 1,9 . cos(π.12/6) = 2 + 1,9 . cos(2π)
y= 2 + 1,9 . cos(360°) = 2 + 1,9 . 1 = 2 + 1,9 = 3,9 m
16) Encontre as soluções das equações trigonométricas seguintes:
a) 3tg x + 4√3 = 5√3 no intervalo [0, 2π]
b) cos²x – 3cos x + 2 = 0 no intervalo 0 ≤ x ≤ π
c) sen 2x – 1/2 = 0 no intervalo 0 ≤ x ≤ π
Solução:
a) 3tg x + 4√3 = 5√3
3tg x = 5√3 - 4√3
3tg x = √3
tg x = √3
3
No intervalo [0, 2π] os ângulos cuja tangente vale √3/3 são 30º e 210º.
S = {30º; 210º}
b) cos²x – 3cos x + 2 = 0
cos x = t
t² - 3t + 2 = 0
t = 1 e t = 2
Como não existe cosseno valendo 2:
cos x = 1
No intervalo 0 ≤ x ≤ π, x = 0.
S = { 0 }
c) sen 2x – 1/2 = 0
sen 2x = 1/2
Os ângulos cujo seno vale 1/2 no intervalo 0 ≤ x ≤ π são 30º e 150º, porém o ângulo da questão é 2x, então:
2x = 30º e 2x = 150º
x = 15º e x = 75º
S = {15º; 75º}
17) (UFRGS) No intervalo [0, π] a equação tg x – 1 = 0:
a) não possui raízes.
b) possui uma única raiz.
c) possui apenas 2 raízes.
d) possui exatamente 4 raízes.
e) apresenta infinitas raízes.
Solução:
tg x – 1 = 0
tg x = 1
Os ângulos onde a tangente vale 1 são 45º e 225º, no intervalo [0, 2π], então, no intervalo [0, π] temos uma única raiz.
Gabarito Letra: B
18) (ITA 2012) Seja x є [0, 2 π] tal que sen(x)cos(x) = 2/5.
Então, o produto e a soma de todos os possíveis valores de tg(x) são, respectivamente
a) 1 e 0
b) 1 e 5/2
c) -1 e 0
d) 1 e 5
e) -1 e -5/2
Solução:
sen(x)cos(x) = 2/5
Dividimos todo mundo por cos²(x), pois surge uma tangente e uma secante ao quadrado que podemos transformar em tangente depois, vejamos como fazemos aparecer o que buscamos:
sen(x)cos(x) = 2/5 cos(x)cos(x) = cos²(x)
tg(x) = 2 . 1 .
5 cos²(x)
tg(x) = 2sec²(x)
5
A identidade trigonométrica diz que:
sec²x = 1 + tg²x
tg(x) = 2/5[1 + tg²(x)]
tg(x) = 2/5 + 2/5tg²(x)
– 2/5tg²(x) + tg(x) – 2/5 = 0
Caímos numa equação do 2º grau, cuja incógnita é tg(x) fazendo a soma e o produto em função de tg(x) chegamos em:
Soma = 5/2 Produto: 1
Gabarito Letra: B
19) Qual o valor máximo da função y = 10 + 5 cos 20x ?
Solução:
O valor máximo da função ocorre quando o fator cos20x é máximo, isto é, quando cos 20x = 1. Logo, o valor máximo da função será y = 10 + 5.1 = 15.
Solução:
Ora, o seno de qualquer arco, é sempre um número real pertencente ao intervalo fechado [-1,1]. Logo, deveremos ter: -1 £ m -1 £ 1 \ 0 £ m £ 2.
Então, o produto e a soma de todos os possíveis valores de tg(x) são, respectivamente
a) 1 e 0
b) 1 e 5/2
c) -1 e 0
d) 1 e 5
e) -1 e -5/2
Solução:
sen(x)cos(x) = 2/5
Dividimos todo mundo por cos²(x), pois surge uma tangente e uma secante ao quadrado que podemos transformar em tangente depois, vejamos como fazemos aparecer o que buscamos:
sen(x)cos(x) = 2/5 cos(x)cos(x) = cos²(x)
tg(x) = 2 . 1 .
5 cos²(x)
tg(x) = 2sec²(x)
5
A identidade trigonométrica diz que:
sec²x = 1 + tg²x
tg(x) = 2/5[1 + tg²(x)]
tg(x) = 2/5 + 2/5tg²(x)
– 2/5tg²(x) + tg(x) – 2/5 = 0
Caímos numa equação do 2º grau, cuja incógnita é tg(x) fazendo a soma e o produto em função de tg(x) chegamos em:
Soma = 5/2 Produto: 1
Gabarito Letra: B
19) Qual o valor máximo da função y = 10 + 5 cos 20x ?
Solução:
O valor máximo da função ocorre quando o fator cos20x é máximo, isto é, quando cos 20x = 1. Logo, o valor máximo da função será y = 10 + 5.1 = 15.
20) Qual o valor mínimo da função y = 3 + 5 sen 2x?
Solução:
O valor mínimo da função ocorre quando o fator sen2x é mínimo, isto é, quando sen2x = -1.
Logo, o valor mínimo da função será y = 3 + 5(-1) = - 2 .
Solução:
O valor mínimo da função ocorre quando o fator sen2x é mínimo, isto é, quando sen2x = -1.
Logo, o valor mínimo da função será y = 3 + 5(-1) = - 2 .
21) Qual o valor máximo da função  ?
?
Solução:
A função terá valor máximo, quando o denominador tiver valor mínimo. Para que o denominador seja mínimo, deveremos ter cos 20x = 1 \
y = 10 / (6 - 2.1) = 10 / 4 = 5/2.
Portanto, o valor máximo da função é 5/2.
Qual seria o valor mínimo da mesma função?
Resposta: 5/4
A função terá valor máximo, quando o denominador tiver valor mínimo. Para que o denominador seja mínimo, deveremos ter cos 20x = 1 \
y = 10 / (6 - 2.1) = 10 / 4 = 5/2.
Portanto, o valor máximo da função é 5/2.
Qual seria o valor mínimo da mesma função?
Resposta: 5/4
22) Para que valores de m a equação sen 30x = m - 1 tem solução?
Solução:
Ora, o seno de qualquer arco, é sempre um número real pertencente ao intervalo fechado [-1,1]. Logo, deveremos ter: -1 £ m -1 £ 1 \ 0 £ m £ 2.
Agora calcule:
a) o valor mínimo da função y = 2 + 9sen4x.
b) o valor máximo da função y = 10 - cosx .
c) o valor de y = sen 180º - cos270º
d) o valor de y = cos 180º - sen 270º
e) o valor de y = cos(360.k) + sen(360.k), para k inteiro.
Respostas: a) - 7 b) 11 c) 0 d) 0 e) 1
a) o valor mínimo da função y = 2 + 9sen4x.
b) o valor máximo da função y = 10 - cosx .
c) o valor de y = sen 180º - cos270º
d) o valor de y = cos 180º - sen 270º
e) o valor de y = cos(360.k) + sen(360.k), para k inteiro.
Respostas: a) - 7 b) 11 c) 0 d) 0 e) 1
23) Encontre a solução da equação cos x + 1 = 0
Solução:
Temos que cos x = - 1. Então x = πrad é uma solução, pois cos π = -1.
Assim, cos x = cos π
Como os arcos de medidas πrad e - πrad possuem a mesma extremidade, o conjunto solução é:
S = {x E R/x = π + 2kπ, k E Z}
24) Ache o o conjunto solução da equação sen (5x) + sen (2x) = 0
Solução:
Observe que é possível transformar o 1º membro em um produto; além disso, o 2º membro é zero. Assim sendo, lembrando que sen p + sen q = 2*sen p + q / 2* cos p - q / 2, temos:
2*sen 5x + 2x /2*cos 5x - 2x /2 = 0 ► sen 7x / 2*cos3x /2 = 0 ► sen 7x/ 2 = 0 ou cos 3x /2 = 0
Para sen 7x/ 2 = sen 0, temos: 7x/ 2 = kπ, k E Z. Portanto: 7x = 2kπ ► x = 2kπ / 7, k E Z
Para cos 3x/ 2 = cos π/2, temos: 3x / 2 = π/ 2 + kπ, k E Z.
Entao: 3x = π + 2kπ ► x = π/ 3 + 2kπ/ 3, k E Z.
O conjunto solução é: S = {x E R/ x = π/3 + 2kπ/ 3 ou x = 2kπ/ 7, k E Z}
Obs: esse mesmo problema poderia ser resolvido assim:
sen (5x) + sen (2x) = 0 ► sen (5x) = - sen (2x)
como: - sen (2x) = sen (- 2x) desse modo temos:
5x = - 2x + 2kπ ou 5x = π - (-2x) + 2kπ, k E Z, daí obtemos:
x = 2kπ/ 7 ou x = π/ 3 + 2kπ/ 3, k E Z
25)
.gif)
Solução:
.gif)
26)
.gif)
Solução:
.gif)
27)
.gif)
Solução:

28)
.gif)
Solução:
.gif)
29) A soma das raízes da equação sen2x=1/2, contidas no intervalo fechado [0,2π], vale:
a) 2π b) 3π c) 4π d) 5π e)6π
Solução:
sen x = 0.5
sen 30 pi/180 = pi/6
(x pertence aos numeros reias tal que x=pi/6+2kpi/k pertence aos numeros inteiro
RESPOSTA: LETRA B
30) Resolva as seguintes equações trigonométricas:
a) 2cosx – 3secx = 5
Solução:
Lembrando que secx = 1/cosx, vem, por substituição:
2.cosx – 3.(1/cosx) – 5 = 0
2.cosx – 3/cosx – 5 = 0
Multiplicando ambos os membros por cosx ¹ 0, fica:
2.cos2x – 3 – 5.cosx = 0
Arrumando convenientemente, teremos:
2.cos2x – 5.cosx – 3 = 0.
Vamos resolver a equação do segundo grau em cosx. Teremos:
Portanto, cosx = 3 ou cosx = -1/2.
A equação cosx = 3 não possui solução, já que o cosseno só pode assumir valores de –1 a +1.
Já para a equação cosx = -1/2, teremos:
cosx = -1/2 = cos120º = cos(2p/3)
Logo,
cosx = cos(2p/3)
Do resultado obtido no item 1.2 acima, poderemos escrever as soluções genéricas da equação dada:
x = 2kp + 2p/3 ou x = 2kp - 2p/3
Estas soluções podem ser reunidas na forma:
x = 2kp ± 2p/3.
Logo, o conjunto solução da equação proposta será:
cosx = -1/2 = cos120º = cos(2p/3)
Logo,
cosx = cos(2p/3)
Do resultado obtido no item 1.2 acima, poderemos escrever as soluções genéricas da equação dada:
x = 2kp + 2p/3 ou x = 2kp - 2p/3
Estas soluções podem ser reunidas na forma:
x = 2kp ± 2p/3.
Logo, o conjunto solução da equação proposta será:
S = {x | x = 2kp ± 2p/3, k inteiro}.
b)3.senx - Ö3.cosx = 0
Solução:
b)3.senx - Ö3.cosx = 0
Solução:
Teremos: 3.senx = Ö3.cosx
Dividindo ambos os membros por cosx ¹ 0, fica:
3.senx/cosx = Ö3.cosx/cosx = Ö3.
3.tgx = Ö3
tgx = Ö3/3 = tg30º = tg(p/6)
Vamos então resolver a equação elementar
tgx = tg(p/6)
Do exposto no item 1.3 acima, vem imediatamente que:
x = kp + p/6.
c) tgx + cotgx = 2
Solução:
Substituindo tgx e cotgx pelos seus valores expressos em função de senx e cosx, vem:
senx/cosx + cosx/senx = 2
Efetuando a operação indicada no primeiro membro, vem:
(sen2x + cos2x)/(senx.cosx) = 2
Como sen2x + cos2x = 1, fica:
1/senx.cosx = 2
1 = 2.senx.cosx
1 = sen2x
sen2x = 1 = sen90º = sen(p/2).
sen2x = sen(p/2)
Aplicando o conhecimento obtido no item 1.1, vem:
2x = (2k+1)p - p/2 OU 2x = 2kp + p/2.
Dividindo ambas as expressões por 2, fica:
x = (2k+1).p/2 - p/4 OU x = kp + p/4.
Simplificando a primeira expressão, vem:
x = kp + p/4 OU x = kp + p/4.
Portanto, x = kp + p/4, que é a solução procurada.
d) 4(sen3x – cos3x) = 5(senx – cosx)
Solução:
Lembrando da identidade:
Solução:
Lembrando da identidade:
A3 – B3 = (A – B) (A2 + AB + B2), poderemos escrever:
4(senx – cosx)(sen2x + senx.cosx + cos2x) = 5(senx - cosx)
4(senx – cosx)(sen2x + senx.cosx + cos2x) = 5(senx - cosx)
Como sen2x + cos2x = 1, vem, substituindo:
4(senx – cosx)(1 + senx.cosx) = 5(senx – cosx)
Simplificando os termos em comum, vem:
4(1 + senx.cosx) = 5
1 + senx.cosx = 5/4
senx.cosx = 5/4 – 1 = 5/4 – 4/4 = 1/4
senx.cosx = 1/4
4(senx – cosx)(1 + senx.cosx) = 5(senx – cosx)
Simplificando os termos em comum, vem:
4(1 + senx.cosx) = 5
1 + senx.cosx = 5/4
senx.cosx = 5/4 – 1 = 5/4 – 4/4 = 1/4
senx.cosx = 1/4
Multiplicando ambos os membros por 2, fica:
2.senx.cosx = 2(1/4)
2.senx.cosx = 1/2
Como já sabemos da Trigonometria que 2.senx.cosx = sen 2x, vem:
sen2x = 1/2 = sen30º = sen(p/6)
sen2x = sen(p/6)
Aplicando o conhecimento obtido no item 1.1 acima, fica:
2x = (2k+1)p - p/6 OU 2x = 2kp + p/6
Dividindo ambas as expressões por 2, vem:
x = (2k+1).p/2 - p/12 OU x = kp + p/12
Simplificando a primeira expressão, fica:
x = kp + 5p/12 OU x = kp + p/12, que é a solução procurada.
Portanto,
S = {x | x = kp + 5p/12 ou x = kp + p/12, k inteiro}.
Solução:
já sabemos que a medida a em graus se relaciona com a medida x em radianos. Colocando: 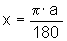 rad, temos:
rad, temos:
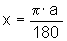 rad, temos:
rad, temos:
Quando a = 30º, temos 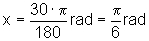
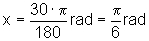
Quando a = 60º, temos 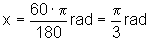
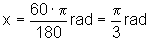
Quando a = 75º, temos 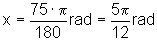
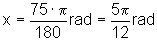
Quando a = -120º, temos 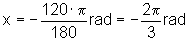
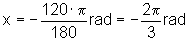
Quando a = 136º, temos 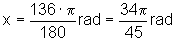
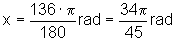
Quando a = 1360º, temos 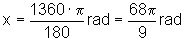
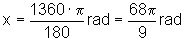
Quando a = -1360º, temos 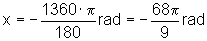
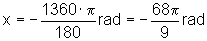
32) Calcule em graus:
3 rad,  rad,
rad, 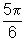 rad,
rad, 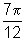 rad, 8 rad.
rad, 8 rad.
 rad,
rad, 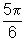 rad,
rad, 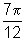 rad, 8 rad.
rad, 8 rad.
Solução:
Já sabemos que a medida a em graus, se relaciona com a medida x em radianos. Colocando: 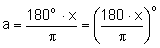 , temos:
, temos:
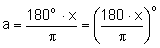 , temos:
, temos:
Quando x=3 rad, temos 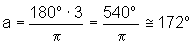
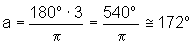
Quando x=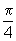 rad, temos
rad, temos 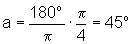
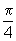 rad, temos
rad, temos 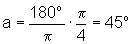
Quando x= 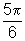 rad, temos
rad, temos 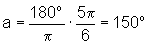
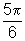 rad, temos
rad, temos 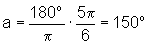
Quando x= 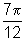 rad, temos
rad, temos 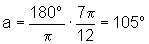
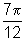 rad, temos
rad, temos 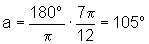
Quando x=8 rad, temos 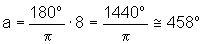
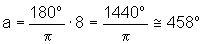
33) Quantas voltas serão dadas na circunferência trigonométrica para se representar os números 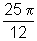 e -12?
e -12?
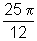 e -12?
e -12?
Solução:
Dado o número real 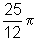 , temos:
, temos:
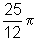 , temos:
, temos: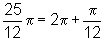
Portanto, para representa-lo será necessário dar uma volta inteira e mais um doze avos de meia volta, no sentido positivo de percurso, isto é, no sentido anti-horário.
Por outro lado, dado o número real -12, temos: 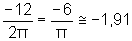 , ou seja, será dada, aproximadamente, uma volta inteira e mais 0,91 de volta no sentido horário, já que o número dado é negativo.
, ou seja, será dada, aproximadamente, uma volta inteira e mais 0,91 de volta no sentido horário, já que o número dado é negativo.
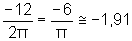 , ou seja, será dada, aproximadamente, uma volta inteira e mais 0,91 de volta no sentido horário, já que o número dado é negativo.
, ou seja, será dada, aproximadamente, uma volta inteira e mais 0,91 de volta no sentido horário, já que o número dado é negativo.
34) (EXTRA-SP) O conjunto dos valores reais de x que tornam verdadeiras a desigualdade
| a) | |
|---|---|
| b) | |
| c) | |
| d) |
Solução:
Usando que:
Para X = x -  , temos
, temos
 | (I) |
|---|
Resolvendo a inequação dada usando (I)

Como 1 - 2 < -1 a inequação proposta não apresenta solução real — porque não existe número real x para que cos2x < -1. Letra D
< -1 a inequação proposta não apresenta solução real — porque não existe número real x para que cos2x < -1. Letra D
35) Resolva a inequação trigonométrica:
| a) | |
|---|---|
| b) | |
| c) | |
| d) |
Solução:

Considerando que
temos que:


Atribuindo valores para k (inteiros) na inequação anterior para verificação de enquadramento ao intervalo proposto:
k
|
intervalo
| |
0
|
convém
| |
1
|
não convém
|
Letra D.
36) Calcule a primeira determinação positiva do conjunto de arcos de mesma extremidade que o arco de medida 38 /3.
/3.
 /3.
/3.
Solução:
Como 2 =6
=6 /3=6.(
/3=6.( /3) e 38
/3) e 38 /3=38.(
/3=38.( /3), então dividindo 38 por 6, obtemos 6 voltas inteiras mais o resto que é 2
/3), então dividindo 38 por 6, obtemos 6 voltas inteiras mais o resto que é 2
 =6
=6 /3=6.(
/3=6.( /3) e 38
/3) e 38 /3=38.(
/3=38.( /3), então dividindo 38 por 6, obtemos 6 voltas inteiras mais o resto que é 2
/3), então dividindo 38 por 6, obtemos 6 voltas inteiras mais o resto que é 2
Multiplicando o resto 2 por  /3, dá a medida do ângulo procurado A=2
/3, dá a medida do ângulo procurado A=2 /3
/3
 /3, dá a medida do ângulo procurado A=2
/3, dá a medida do ângulo procurado A=2 /3
/3
37) Verifique se os arcos de medidas 7 /3 e 19
/3 e 19 /3 são arcos côngruos?
/3 são arcos côngruos?
 /3 e 19
/3 e 19 /3 são arcos côngruos?
/3 são arcos côngruos?
Solução:
d=19
 /3-7
/3-7 /3=4
/3=4
que é um múltiplo de 2
 , então os arcos são côngruos.
, então os arcos são côngruos.
38) No triângulo a seguir temos dois ângulos, um medindo 45º, outro medindo 105º, e um dos lados medindo 90 metros. Com base nesses valores determine a medida de x.
.jpg)
Solução:
Para determinarmos a medida de x no triângulo devemos utilizar a lei dos senos, mas para isso precisamos descobrir o valor do terceiro ângulo do triângulo. Para tal cálculo utilizamos a seguinte definição: a soma dos ângulos internos de um triângulo é igual a 180º. Portanto:
α + 105º + 45º = 180º
α + 150º = 180º
α = 180º – 150º
α = 30º
Aplicando a lei dos senos
.jpg)
39) Calcule a medida da maior diagonal do paralelogramo da figura a seguir, utilizando a lei dos cossenos.
α + 105º + 45º = 180º
α + 150º = 180º
α = 180º – 150º
α = 30º
Aplicando a lei dos senos
.jpg)
39) Calcule a medida da maior diagonal do paralelogramo da figura a seguir, utilizando a lei dos cossenos.
.jpg)
Solução:
cos 120º = –cos(180º – 120º) = – cos 60º = – 0,5
x² = 5² + 10² – 2 * 5 * 10 * ( – cos 60º)
x² = 25 + 100 – 100 * (–0,5)
x² = 125 + 50
x² = 175
√x² = √175
x = √5² * 7
x = 5√7
Portanto, a diagonal do paralelogramo mede 5√7 cm.
40) Qual o valor máximo da função y = 10 + 5 cos 20x ?
Solução:
O valor máximo da função ocorre quando o fator cos20x é máximo, isto é, quando cos 20x = 1. Logo, o valor máximo da função será y = 10 + 5.1 = 15.
41) Um alpinista deseja calcular a altura de uma encosta que vai escalar. Para isso, afasta-se, horizontalmente, 80 m do pé da encosta e visualiza o topo sob um ângulo de 55º com o plano horizontal. Calcule a altura da encosta. (Dados: sem 55º = 0,81, cos 55º = 0,57 e tg 55º = 1,42)
Resp: 113,6m
Fonte: www.numerofilia.com.br
oi muuuuuu
ResponderExcluiranonimo vaca
olhe so gostei porq ure tinha um auqestao que era igual a minha se nao num ia gustar nau m gustei na verdade
ResponderExcluir[
Boa noite, na questão 07, a resposta não seria 2 raiz de 13 em vez de 2 raiz de 3 como está la?
ResponderExcluirbom dia agradeço bastante pelo conteúdo oferecido, me ajudou muito....
ResponderExcluirobrigado....
Não encontrei o que estava procurando
ResponderExcluirUma questão de trigonometria UFSM 2016
ResponderExcluirbom dia grupo, ops site
ResponderExcluirbenção chat
Rum
ResponderExcluirGostaria que tivesse preparado um conteúdo de trigonometria. Mesmo ter estudado, não consegui fazer nada disso.
ResponderExcluir