Equação geral da reta
Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos.
Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos de r e P(x,y) um ponto genérico, também de r, estando A, B e P alinhados, podemos escrever:
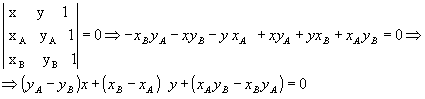
Fazendo yA - yB = a, xB - xA = b e xAyB - xByA=c, como a e b não são simultaneamente nulos 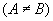 , temos:
, temos:
ax + by + c = 0
|
(equação geral da reta r)
Essa equação relaciona x e y para qualquer ponto P genérico da reta. Assim, dado o ponto P(m, n):
- se am + bn + c = 0, P é o ponto da reta;
- se am + bn + c
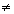 0, P não é ponto da reta.
0, P não é ponto da reta.
Acompanhe os exemplos:
- Vamos considerar a equação geral da reta r que passa por A(1, 3) e B(2, 4).
Considerando um ponto P(x, y) da reta, temos:
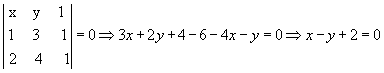
- Vamos verificar se os pontos P(-3, -1) e Q(1, 2) pertencem à reta r do exemplo anterior. Substituindo as coordenadas de P em x - y + 2 = 0, temos:
-3 - (-1) + 2 = 0 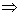 -3 + 1 + 2 = 0
-3 + 1 + 2 = 0
Como a igualdade é verdadeira, então P 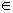 r.
r.
Substituindo as coordenadas de Q em x - y + 2 = 0, obtemos:
1 - 2 + 2 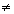 0
0
Como a igualdade não é verdadeira, então Q 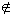 r.
r.
Equação segmentária
Considere a reta r não paralela a nenhum dos eixos e que intercepta os eixos nos pontos P(p, 0) e Q(0, q), com 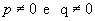 :
:
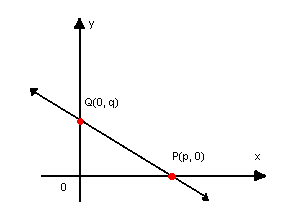
A equação geral de r é dada por:
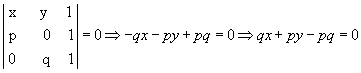
Dividindo essa equação por pq 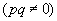 , temos:
, temos:
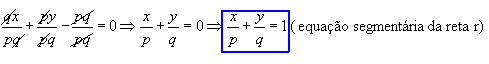
Como exemplo, vamos determinar a equação segmentária da reta que passa por P(3, 0) e Q(0, 2), conforme o gráfico:
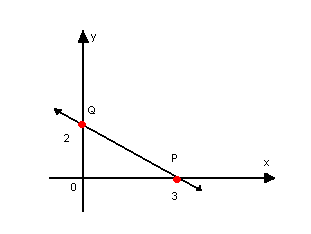 | 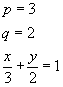 |
Exemplo: Determine a equação segmentária da reta t: 7x + 14y – 28 =0 e as coordenadas dos pontos de interseção da reta com os eixos do plano.
Solução:
Solução:
Para determinar a forma segmentária da equação da reta t devemos isolar o termo independente c. Assim, teremos:
7x + 14y = 28
Dividindo toda igualdade por 28, obtemos:

Que é a equação segmentária da reta t.
Com a equação segmentária, podemos determinar os pontos de interseção da reta com os eixos ordenados do plano. O termo que divide x na equação segmentária é abscissa do ponto de intercessão da reta com o eixo x, e o termo que divide y é abscissa do ponto de interseção da reta com o eixo y. Assim:
(4, 0) é o ponto de interseção da reta com o eixo x.
(0, 2) é o ponto de interseção da reta com o eixo y.
7x + 14y = 28
Dividindo toda igualdade por 28, obtemos:

Que é a equação segmentária da reta t.
Com a equação segmentária, podemos determinar os pontos de interseção da reta com os eixos ordenados do plano. O termo que divide x na equação segmentária é abscissa do ponto de intercessão da reta com o eixo x, e o termo que divide y é abscissa do ponto de interseção da reta com o eixo y. Assim:
(4, 0) é o ponto de interseção da reta com o eixo x.
(0, 2) é o ponto de interseção da reta com o eixo y.
Equação reduzida da reta
Podemos representar uma reta no plano cartesiano por meio da condição geométrica ou por uma equação matemática. Em relação à equação matemática, a reta pode ser escrita nas seguintes formas: reduzida, segmentária, geral ou paramétrica. Vamos abordar a representação de uma equação reduzida de reta, demonstrando três possíveis situações.
Vamos considerar a equação da reta que passa por um ponto Q (x1, y1), com coeficiente angular a, observe:
y – y1 = a * (x – x1)
Escolhendo ao acaso, o ponto (0, b) e determinando que a reta o intersecte, temos que:
y – b = a * (x – 0)
y – b = a * x – a * 0
y – b = ax
y = ax + b
Portanto, a equação reduzida da reta possui a seguinte lei de formação:
Vamos considerar a equação da reta que passa por um ponto Q (x1, y1), com coeficiente angular a, observe:
y – y1 = a * (x – x1)
Escolhendo ao acaso, o ponto (0, b) e determinando que a reta o intersecte, temos que:
y – b = a * (x – 0)
y – b = a * x – a * 0
y – b = ax
y = ax + b
Portanto, a equação reduzida da reta possui a seguinte lei de formação:
y = ax +b
.jpg)
Exemplo 1:
Utilizando o ponto P1(2, 7), no qual x = 2 e y = 7, temos:
y – y1 = a * (x – x1)
y – 7 = 4 * (x – 2)
y – 7 = 4x – 8
y = 4x – 8 + 7
y = 4x – 1
Exemplo 2:
Utilizando o ponto P1(2, 7), no qual x = 2 e y = 7, temos:
y – y1 = a * (x – x1)
y – 7 = 4 * (x – 2)
y – 7 = 4x – 8
y = 4x – 8 + 7
y = 4x – 1
Exemplo 2:
A forma geral da equação reduzida da reta é dada pela expressão: y = ax + b. Utilizando o ponto P1(2, 7), temos:
y = ax + b
7 = a * 2 + b
2a + b = 7
Utilizando o ponto P2(–1, –5), temos:
–5 = a * (–1) + b
–5 = –a + b
–a + b = –5
Resolvendo o sistema,
.jpg)
Substituindo os valores de a e b na expressão matemática, temos:
y = ax + b
y = 4x – 1
Exemplo 3:
Podemos construir uma matriz quadrada com os pontos fornecidos e um ponto genérico (x, y). O determinante dessa matriz será a equação da reta. Observe:
P1(2, 7) e P2(–1, –5)
y = ax + b
y = 4x – 1
Exemplo 3:
Podemos construir uma matriz quadrada com os pontos fornecidos e um ponto genérico (x, y). O determinante dessa matriz será a equação da reta. Observe:
P1(2, 7) e P2(–1, –5)
.jpg)
Aplicando Sarrus: produto dos termos da diagonal principal subtraído do produto dos termos da diagonal secundária.
.jpg)
[(x * 7 * 1) + (–1 * 1 * y) + (–5 * 2 * 1)] – [(–1 * 7 * 1) + (y * 2 * 1) + (–5 * x * 1)] = 0
[7x – y –10] – [–7 + 2y – 5x] = 0
7x – y – 10 + 7 – 2y + 5x = 0
12x – 3y – 3 = 0
–3y = –12x + 3 (dividir todos por – 3)
y = 4x – 1
[7x – y –10] – [–7 + 2y – 5x] = 0
7x – y – 10 + 7 – 2y + 5x = 0
12x – 3y – 3 = 0
–3y = –12x + 3 (dividir todos por – 3)
y = 4x – 1
Retas perpendiculares
Sabemos da Geometria Plana que duas retas são perpendiculares quando são concorrentes e formam entre si um ângulo reto (90º) . Sejam as retas r: y = mr x + nr e s: y = ms x + ns . Nestas condições podemos escrever a seguinte relação entre os seus coeficientes angulares:
ms = - 1 / mr ou mr . ms = -1 .
Dizemos então que se duas retas são perpendiculares, o produto dos seus coeficientes angulares
é igual a -1.
Exemplo:
Dadas as retas de equações (2w - 2)x + (w - 1)y + w = 0 e (w - 3)y + x - 2w = 0, podemos afirmar que:
a) elas são perpendiculares para qualquer valor de w
b) elas são perpendiculares se w = 1
c) elas são perpendiculares se w = -1
d) elas são perpendiculares se w = 0
e) essas retas não podem ser perpendiculares
Solução:
Podemos escrever para a 1ª reta: y = [-(2w-2) / (w-1)].x - w /(w-1).
Analogamente para a 2ª reta: y = [-1 / (w-3)].x + 2w / (w-3). Ora, os coeficientes de x são os coeficientes angulares e, pelo que já sabemos, a condição de perpendicularidade é que o produto desses coeficientes angulares seja igual a -1. Logo:
Efetuando os cálculos indicados e simplificando-se obtemos: w2 - 2w + 1 = 0, que é equivalente a
(w - 1)2 = 0, de onde conclui-se que w = 1.
Mas, cuidado! Observe que 1 anula o denominador da expressão acima e, portanto é uma raiz estranha, já que não existe divisão por zero! Apesar das aparências, a raiz 1 não serve! Logo, a alternativa correta é a letra E e não a letra B como ficou aparente.
Fontes: www.mundoeducacao.com.br
Questões resolvidas sobre equação geral e reduzida da reta e retas perpendiculares
1) Determine a equação reduzida da reta t que forma um ângulo de 135o com o eixo das abscissas e que passa pelo ponto P(4, 5).
Sabemos que α = 135o e que a equação reduzida da reta é da forma y = mx + q. Assim, temos que:
m = tg 135o = – 1
Como a reta t passa pelo ponto P, obtemos:
5 = -1*4 + q
q = 5 + 4 = 9
Portanto, a equação reduzida da reta t é y = – x + 9.
2) Determine a equação reduzida da reta s que passa pelos pontos A(1, 0) e B(3, 4).
m = tg 135o = – 1
Como a reta t passa pelo ponto P, obtemos:
5 = -1*4 + q
q = 5 + 4 = 9
Portanto, a equação reduzida da reta t é y = – x + 9.
2) Determine a equação reduzida da reta s que passa pelos pontos A(1, 0) e B(3, 4).
Solução:
Como conhecemos dois pontos da reta s, podemos encontrar sua equação geral.
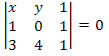
Desenvolvendo o determinante obtemos:
2y – 4x + 4 = 0
Isolando y teremos:
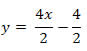
Ou
y = 2x – 2
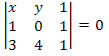
Desenvolvendo o determinante obtemos:
2y – 4x + 4 = 0
Isolando y teremos:
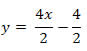
Ou
y = 2x – 2
3) Calcule o coeficiente angular das retas de equações:
a) 3x + 4y - 7 = 0
b) -6x + 8y + 3 = 0
Solução:
a) 4y = -3x + 7
y = -3 x + 7 coeficiente angular = -3
4 4 4
b) 8y = 6x - 3
y = 6 x - 3 = 3 x - 3 coeficiente angular = 3
8 8 4 8 4
4) Ache a equação segmentária da reta de equação geral 2x + 3y - 18 = 0.
Solução:
Podemos escrever: 2x + 3y = 18 ; dividindo ambos os membros por 18 vem:
2x/18 + 3y/18 = 18/18 \ x / 9 + y / 6 = 1.
Vemos, portanto que p = 9 e q = 6 e portanto a reta corta os eixos coordenados nos pontos A(9,0) e B(0,6).
5) Um móvel descreve uma trajetória retilínea e suas coordenadas em função do tempo t , são:
x = 3t + 11y = -6t - 21
Qual a equação segmentária dessa trajetória?
Solução:
Multiplicando ambos os membros da 1ª equação paramétrica por 2, vem: 2x = 6t + 22. Somando agora membro a membro com a 2ª equação, obtemos: 2x + y = 32 (observe que a variável t é eliminada nessa operação pois 6t + ( -6t ) = 0 ). Dividindo ambos os membros da equação obtida por 32 fica:
2x / 32 + y / 32 = 32 / 32 \ x / 16 + y / 32 = 1, que é a equação segmentária procurada.
6) Determine a equação geral da reta sabendo que os pontos A(2,1) e B(- 2,4) pertencem a reta.
Com dois pontos podemos determinar a equação da reta:
y = ax + b
*1 = 2a + b
*4 = -2a + b (+)
5 = b
2a + b = 1
2a + 5 = 1
2a = - 4
a = - 2
Logo a equação da reta é y = - 2x + 5, passando para a forma de equação geral fica:
2x + y - 5 = 0
7) A reta r é perpendicular à reta s. Sabendo-se que a reta s possui o seu coeficiente ângular igual à 1/2 e que a reta r passa pelo ponto A(5,3), determine a equação geral da reta r.
Solução:
Para determinarmos a equação geral da reta r, necessitaremos do seu coeficiente ângular e de um ponto. Como as retas r e s são perpendiculares, logo o produto de seus coeficientes é igual à -1.
mr * ms = - 1
mr * (1/2) = - 1
mr = - 2
Reta r : mr = - 2 ; A(5,3)
y - yo = m(x - xo)
y - 3 = - 2(x - 5)
y - 3 = - 2x + 10
y = - 2x + 13
2x + y - 13 = 0
Para determinarmos a equação geral da reta r, necessitaremos do seu coeficiente ângular e de um ponto. Como as retas r e s são perpendiculares, logo o produto de seus coeficientes é igual à -1.
mr * ms = - 1
mr * (1/2) = - 1
mr = - 2
Reta r : mr = - 2 ; A(5,3)
y - yo = m(x - xo)
y - 3 = - 2(x - 5)
y - 3 = - 2x + 10
y = - 2x + 13
2x + y - 13 = 0
8) Determine a equação da reta que passa pelo ponto P (-1, -2) e forma com os eixos coordenados um triângulo de área 4 u.a.
Solução:
Seja m o coeficiente angular da reta:
y - (-2) = m*[x - (-1) -----> y = mx + m - 2
Para x = 0 ----> y = m - 2
Para y = 0 ----> x = - (m - 2)/m
S = x*y ----> S = - [(m - 2)/m]*(m - 2)/2 ----> 4 = - (m - 2)²/2m ----> 8m = - (m - 2)² ----> 8m = - m² + 4m - 4 -----> m² + 4m + 4 = 0
Raiz dupla ----> m = - 2
Reta ----> y = - 2x - 2 - 2 -----> y = - 2x - 4
y - (-2) = m*[x - (-1) -----> y = mx + m - 2
Para x = 0 ----> y = m - 2
Para y = 0 ----> x = - (m - 2)/m
S = x*y ----> S = - [(m - 2)/m]*(m - 2)/2 ----> 4 = - (m - 2)²/2m ----> 8m = - (m - 2)² ----> 8m = - m² + 4m - 4 -----> m² + 4m + 4 = 0
Raiz dupla ----> m = - 2
Reta ----> y = - 2x - 2 - 2 -----> y = - 2x - 4
9) (PUC) Determine a equação da reta com coeficiente angular igual a - 4/5, e que passa pelo ponto p (2, -5).
Solução:
Y = - 4X / 5 + b <~~~~coeficiente angular igual a - 4/5
...que passa em (2,-5)...
-5 = - 4x2 / 5 + b
b = -5 + 8/5
b = (8-25) /5
b = - 17/5 <~~~~
............
Y = - 4X / 5 - 17/5
5Y = - 4X - 17
10) Considere no plano cartesiano uma reta r de equação 3x + 5y +1 =0 e um ponto Q de coordenadas (5,5). Determine a equação da resta s perpendicular a r passando por Q.
Solução:
.gif)
Solução:
.gif)
12) Prove que as retas s: x + 2y – 1 = 0 e r: 4x – 2y +12 = 0 são perpendiculares.
Solução:
.gif)
13) (UFSC) De acordo com o gráfico abaixo, assinale a(s)
proposição(ões) VERDADEIRA(S).
01. A equação da reta s é 3x – 2y + 6 = 0.
02. A reta s e a reta r são perpendiculares.
04. As retas r e s se interceptam no ponto de abscissa 4/5.
08. A área da região do plano limitada pelas retas r, s e pelo eixo das abscissas é igual a 3/10 unidades área.
Solução:
01 – Conforme o gráfico, a reta s intercepta o eixo x no ponto -2, então já temos um ponto, que é (-2,0).
O outro ponto é (0,3), pois é onde a reta corta o eixo y.
Com esses dois pontos fica fácil obter a equação da reta com os dois pontos e um terceiro (x,y) sendo a área desses ponto igual a zero, para que seja uma reta:
|0 -2 x 0| = 0
|3 0 y 3 |
-2y+3x+6 = 0
Preposição verdadeira
02 – Para que as retas sejam perpendiculares, seus coeficientes angulares devem ser opostos e inversos.
Para obter o coeficiente angular, devemos observar a equação reduzida das duas retas, vejamos na reta s:
-2y+3x+6 = 0
2y = 3x+6
y = 3x+3
2
O coeficiente angular será 3/2, o coeficiente de x.
Na reta r devemos encontrar a equação reduzida, sabemos que ela é representada por:
y = ax+b
Sabemos pelo gráfico que quando x é 0 y é 1, portanto:
1 = 0.a+b
b = 1
Portanto:
y = ax+1
Quando y = 0, x = 1. Logo:
0 = a.1+1
a = -1
Como a é -1, esse é o coeficiente angular da reta.
Com -1 e 3/2 não temos oposto nem inverso.
Ítem falso
04 – Para que as retas interceptem-se no ponto x=4/5, lembra que abscissa é x, abXissa, aplicando esse ponto em x na equação reduzida das retas, y deve ter o mesmo valor nas duas:
Reta s
y = 3x+3
2
y = 3. 4 + 3
2 5
y = 12 + 1
10
y = 22
10
y = 11
5
Reta r
y = -x+1
y = -4 + 1
5
y = 1
5
Ítem falso
08 – Será a área por coordenadas entre os pontos (-2, 0); (1,0) e o ponto de intersecção das duas retas, que é o ponto comum entre as duas, para achar esse ponto, resolvemos as duas equações de reta como um sistema linear, achando x e y que é comum aos dois:
y = 3x+3 y = -x+1
2
y = -x+1
Substituindo y pelo seu valor na primeira reta:
3x+3 = -x+1
2
-2x+2 = 3x+3
5x = 1
x = 1/5
y = -x+1
y = -1+1
5
y = 4/5
O ponto é (1/5, 4/5) e a área será:
A = 1/2|-2 1 1/5 -2|
| 0 0 4/5 0|
A = 1/2 |4/5+8/5|
A = 1/2. 12/5
A = 12/10
A = 6/5
Falso
Soma dos ítens verdadeiros: 01
14) (UDESC 2008) A soma do coeficiente angular com o coeficiente linear da reta que passa pelos pontos A(1, 5) e B(4, 14) é:
a) 4
b) -5
c) 3
d) 2
e) 5
15) (ADVISE 2009) A equação geral da reta tangente à curva y = x² + x no ponto de abscissa 1 é:
a) 3x – y – 1 = 0
b) 3x – y = 0
c) 2x – y – 1 = 0
d) 2x – y = 0
e) 5x – 2y – 2 = 0
16) (USP) A equação da reta perpendicular ao eixo das abscissas que passa pelo ponto médio do segmento AB, onde A(2, 3) e B é o centro da circunferência de equação x2 + y2 - 8x - 6y + 24 = 0, é:
a) y = 3
b) y = 4
c) x = 4
d) x = 3
e) 3x + 4y = 0
17) Determinar as equações das retas (t) tangentes à circunferência x² + y² + 2x - 3 = 0 e que passam pelo ponto P(5, 2). Resp: y - 2 = 0 e 3x - 4y - 7 = 0

ótimo
ResponderExcluiresse blog é muito boooom!!! obrigada!
ResponderExcluirESSE BLOG E SHOW, MUITO MAIS MUITO BOM MESMO.
ResponderExcluirConsiderando o modelo gráfico de Y²-x+1=0 e o ponto Q(2,-1). A equação da reta tangente a este ponto do modelo gráfico é?
ResponderExcluirQuem pode me ajudar nessa?
Ajudaria muito mais se as questões tivessem um cunho prático. Questões contextualizadas, que construíssem, de fato, aprendizagem significativa para os estudantes.
ResponderExcluir