Lançamento Vertical e Queda Livre
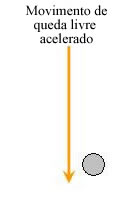
Denomina-se Queda Livre o movimento vertical, próximo à superfície da Terra, quando um corpo de massa m é abandonado no vácuo ou em uma região onde desprezamos a resistência do ar.
A queda livre é um movimento uniformemente variado, sua aceleração é constante e igual a 9,8 m/s2 (ao nível do mar), chamada de aceleração gravitacional.
Na queda, o módulo da velocidade do corpo aumenta, o movimento é acelerado, e, portanto, o sinal da aceleração é positivo.
A queda livre é um movimento uniformemente variado, sua aceleração é constante e igual a 9,8 m/s2 (ao nível do mar), chamada de aceleração gravitacional.
Na queda, o módulo da velocidade do corpo aumenta, o movimento é acelerado, e, portanto, o sinal da aceleração é positivo.
Equação horária do espaço na queda livre:
.jpg)
Onde: g é a aceleração da gravidade
t é o tempo de queda.
S é a altura
Equação horária da velocidade na queda livre:
.jpg){kind=small}
Onde: v é a velocidade
Equação de Torricelli para a queda livre.
.jpg){kind=small}
Quando um corpo é arremessado para cima ou para baixo, com uma velocidade inicial não nula, chamamos o movimento de Lançamento vertical. Esse movimento também é um movimento uniformemente variado como na queda livre, em que a aceleração é a da gravidade.
Lançamento vertical para cima
À medida que um corpo lançado para cima sobe, sua velocidade escalar diminui até que se anule no ponto de altura máxima. Isso ocorre porque o movimento é retardado, ou seja, o movimento se dá contra a ação da gravidade.
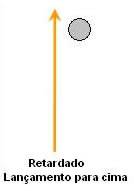
Lançamento vertical para baixo
Ao contrário do lançamento vertical para cima, o lançamento vertical para baixo é um movimento acelerado, pois está na mesma direção e sentido da aceleração gravitacional. Assim, a velocidade de um corpo lançado verticalmente para baixo aumenta à medida que o corpo desce.
As funções horárias do lançamento vertical são:
Função horária do espaço
.jpg)
Função horária da velocidade
.jpg){kind=small}
Equação de Torricelli
.jpg){kind=small}
Para o lançamento para baixo, a aceleração é positiva (g > 0), enquanto para o lançamento para cima a aceleração é negativa (g < 0).
Questões resolvidas sobre Lançamento vertical e Queda Livre
01- ( UFMG ) Um gato consegue sair ileso de muitas quedas. Suponha que a maior velocidade com a qual ele possa atingir o solo sem se machucar seja de 8 m/s. Então, desprezando a resistência do ar, a altura máxima de queda, para que o gato nada sofra, deve ser:
02- (Mackenzie-SP) Um projétil de brinquedo é arremessado verticalmente para cima, da beira da sacada de um prédio, com uma velocidade inicial de 10m/s. O projétil sobe livremente e, ao cair, atinge a calçada do prédio com velocidade igual a 30m/s. Determine quanto tempo o projétil permaneceu no ar. Adote g = 10m/s² e despreze as forças dissipativas.
03-(CEFET-CE) Duas pedras são lançadas do mesmo ponto no solo no mesmo sentido. A primeira tem velocidade inicial de módulo 20 m/s e forma um ângulo de 60° com a horizontal, enquanto, para a outra pedra, este ângulo é de 30°. O módulo da velocidade inicial da segunda pedra, de modo que ambas tenham o mesmo alcance, é:
DESPREZE A RESISTÊNCIA DO AR.
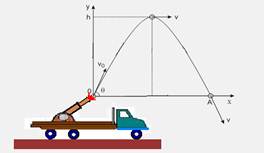
04-(CEFET-CE) Um caminhão se desloca em movimento retilíneo e horizontal, com velocidade constante de 20m/s. Sobre sua carroceria, está um canhão, postado para tiros verticais, conforme indica a figura. A origem do sistema de coordenadas coincide com a boca do canhão e, no instante t=0, ele dispara um projétil, com velocidade de 80m/s. Despreze a resistência do ar e considere g=10m/s2.
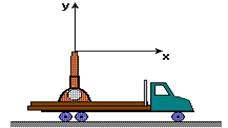
Determine o deslocamento horizontal do projétil, até ele retornar à altura de lançamento, em relação:
a) ao caminhão;
b) ao solo.
05-(Ufms-MS) Em um lançamento oblíquo (trajetória mostrada na figura a seguir) em um local onde a aceleração constante da gravidade é g, sejam respectivamente, H, X e β a altura máxima, o alcance horizontal e o ângulo de lançamento do projétil, medido em relação ao eixo horizontal x. Desprezando-se a resistência do ar, é correto afirmar que
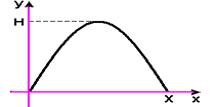
(01) o tempo para que se alcance X é igual ao tempo de subida do projétil.
(02) o tempo para que se alcance X é igual ao dobro do tempo de descida do projétil.
(04) se tg(β) = 4, então H = X.
(08) a energia cinética do projétil é máxima quando é atingida a altura máxima.
(16) a energia mecânica do projétil aumenta no trecho de descida.
06-(CEFET-CE) Um aluno do CEFET em uma partida de futebol lança uma bola para cima, numa direção que forma um ângulo
de 60° com a horizontal. Sabendo que a velocidade na altura máxima é 20 m/s, podemos afirmar que a velocidade de lançamento da bola, em m/s, será:
a) 10 b) 17 c) 20 d) 30 e) 40
07-(PUCCAMP-SP) Observando a parábola do dardo arremessado por um atleta, um matemático resolveu obter uma expressão
que lhe permitisse calcular a altura y, em metros, do dardo em relação ao solo, decorridos t segundos do instante de seu lançamento (t = 0). Se o dardo chegou à altura máxima de 20 m e atingiu o solo 4 segundos após o seu lançamento, então, desprezada a altura do atleta, considerando g=10m/s2, a expressão que o matemático encontrou foi
a) y = - 5t2 + 20t b) y = - 5t2 + 10t c) y = - 5t2 + t d) y = -10t2+ 50 e) y = -10t2 + 10
08-(Ufpe-PE) Um projétil é lançado obliquamente no ar, com velocidade inicial vo = 20 m/s, a partir do solo. No ponto mais alto de sua trajetória, verifica-se que ele tem velocidade igual à metade de sua velocidade inicial. Qual a altura máxima, em metros, atingida pelo projétil? (Despreze a resistência do ar e considere g=10m/s2).
09-(FUVEST-SP) Durante um jogo de futebol, um chute forte, a partir do chão, lança a bola contra uma parede próxima. Com auxílio de uma câmera digital, foi possível reconstituir a trajetória da bola, desde o ponto em que ela atingiu sua altura máxima (ponto A) até o ponto em que bateu na parede (ponto B). As posições de A e B estão representadas na figura. Após o choque, que é elástico, a bola retorna ao chão e o jogo prossegue.
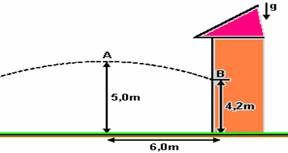
a) Estime o intervalo de tempo t1, em segundos, que a bola levou para ir do ponto A ao ponto B.
b) Estime o intervalo de tempo t2, em segundos, durante o qual a bola permaneceu no ar, do instante do chute até atingir o chão após o choque.
c) Represente, em sistema de eixos, em função do tempo, as velocidades horizontal Vx e vertical Vy da bola em sua trajetória, do instante do chute inicial até o instante em que atinge o chão, identificando por Vx e Vy, respectivamente, cada uma das curvas.
NOTE E ADOTE:
Vy é positivo quando a bola sobe
Vx é positivo quando a bola se move para a direita
10-(PUCCAMP-SP) Um atleta arremessa um dardo sob um ângulo de 45° com a horizontal e, após um intervalo de tempo t, o
dardo bate no solo 16 m à frente do ponto de lançamento. Desprezando a resistência do ar e a altura do atleta, o intervalo de tempo t, em segundos, é um valor mais próximo de:
Dados: g = 10 m/s2 e sen 45° = cos 45° = 0,7
a) 3,2 b) 1,8 c) 1,2 d) 0,8 e) 0,4
11- Ufjf-MG) Durante uma partida de futebol, um jogador, percebendo que o goleiro do time adversário está longe do gol, resolve tentar um chute de longa distância (vide figura). O jogador se encontra a 40 m do goleiro. O vetor velocidade inicial da bola tem módulo Vo = 26 m/s e faz um ângulo de 25° com a horizontal, como mostra a figura a seguir.
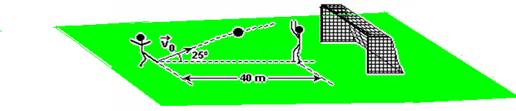
Desprezando a resistência do ar, considerando a bola pontual e usando cos 25° = 0,91, sen 25° = 0,42 e g=10m/s2:
a) Faça o diagrama de forças sobre a bola num ponto qualquer da trajetória durante o seu vôo, após ter sido chutada. Identifique a(s) força(s).
b) Saltando com os braços esticados, o goleiro pode atingir a altura de 3,0 m. Ele consegue tocar a bola quando ela passa sobre ele? Justifique.
c) Se a bola passar pelo goleiro, ela atravessará a linha de gol a uma altura de 1,5 m do chão. A que distância o jogador se encontrava da linha de gol, quando chutou a bola? (Nota: a linha de gol está atrás do goleiro.)
12-(CEFET-CE) Uma roda de raio R rola uniformemente, sem escorregar, ao longo de uma superfície horizontal. Do ponto A da roda se desprende uma gota de barro, como mostra a figura a seguir.
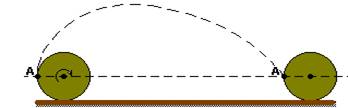
Com que velocidade v deve se deslocar a roda, se a gota, depois de lançada ao espaço, volta a cair sobre o mesmo ponto da roda após efetuar uma volta? Considere desprezível a resistência do ar.
13-(UNICAMP-SP) Uma bola de tênis rebatida numa das extremidades da quadra descreve a trajetória representada na figura a seguir, atingindo o chão na outra extremidade da quadra. O comprimento da quadra é de 24 m.
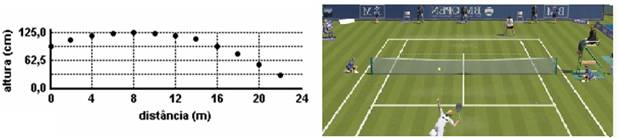
a) Calcule o tempo de vôo da bola, antes de atingir o chão. Desconsidere a resistência do ar nesse caso.
b) Qual é a velocidade horizontal da bola no caso acima?
c) Quando a bola é rebatida com efeito, aparece uma força, FE, vertical, de cima para baixo e igual a 3 vezes o peso da bola. Qual será a velocidade horizontal da bola, rebatida com efeito para uma trajetória idêntica à da figura?
14-(UNICAMP-SP) O famoso salto duplo twistcarpado de Daiane dos Santos foi analisado durante um dia de treinamento no Centro Olímpico em Curitiba, através de sensores e filmagens que permitiram reproduzir a trajetória do centro de gravidade de Daiane na direção vertical (em metros), assim como o tempo de duração do salto.
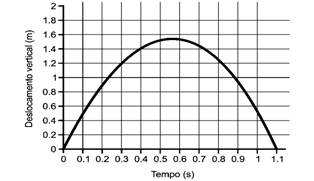
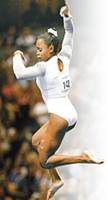
De acordo com o gráfico, determine:
a) A altura máxima atingida pelo centro de gravidade de Daiane.
b) A velocidade média horizontal do salto, sabendo-se que a distância percorrida nessa direção é de 1,3m.
c) A velocidade vertical de saída do solo.
15-(PUC-SP) Futebol é, sem dúvida, o esporte mais popular de nosso país. Campos de futebol são improvisados nas ruas, nas praças, nas praias. Já os campos de futebol profissional são projetados e construídos seguindo regras e dimensões bem definidas
O comprimento do campo pode variar de um mínimo de 90m até um máximo de 120m, enquanto a medida da largura pode variar entre 45m e 90m. De qualquer maneira, independentemente das dimensões do campo, a distância entre as traves verticais de um mesmo gol é de 7,3m, e a grande área do campo, dentro da qual ficam o goleiro e as traves, tem as medidas assim definidas:
"A grande área, ou área penal, está situada em ambas as extremidades do campo e será demarcada da seguinte maneira: serão traçadas duas linhas perpendiculares à linha de meta, a 16,5m de cada trave do gol. Essas linhas se adentrarão por 16,5m no campo e se unirão a uma linha paralela à linha de meta. Em cada grande área será marcado um ponto penal, a 11,0m de distância a partir do ponto médio da linha entre as traves, eqüidistantes às mesmas, Por fora de cada grande área será traçado um semicírculo com raio de 9,2m a partir de cada ponto penal." (fig. 1)
Para alcançar o gol, os jogadores lançam mão de várias técnicas e fundamentos. Dentre esses fundamentos, um dos mais difíceis de serem executados pelos jogadores, e que está diretamente ligado às medidas do campo, é o 'lançamento'. Nestas jogadas, em que se destacaram Gerson e Pelé, dentre outros, um jogador chuta a bola que, a partir daí, sobe, descreve uma parábola sob a ação da gravidade e vai alcançar outro jogador, uns tantos metros à frente.
Instruções: Nas respostas lembre-se de deixar os processos de resolução claramente expostos.
Não basta escrever apenas o resultado final. É necessário registrar os cálculos e/ou raciocínio utilizado.
Sempre que necessário, utilize: g = 10m/s2, sen 20° = 0,35 e cos 20° = 0,95
Nas questões seguintes, eventualmente, você precisará de dados numéricos contidos no texto. Procure-os com atenção.
Para as questões seguintes, considere a fig. 2 , na qual um jogador chuta a boa com velocidade de módulo 72 km/h e em um ângulo de 20° em relação à horizontal. A distância inicial entre a bola e a barreira é de 9,5m e entre a bola e a linha do gol, 19m. A trave superior do gol encontra-se a 2,4m do solo.
Considere desprezível o trabalho de forças dissipativas sobre a bola.
a) Determine qual é a máxima altura que a barreira pode ter para que a bola a ultrapasse.
b) Determine a distância entre a trave superior e a bola, no instante em que ela entra no gol.
c) A trajetória da bola chutada pelo jogador da figura pode ser descrita pela equação y = 7/19x - (5/361)x2, na qual 'y' é a medida, em metros, da altura em que a bola se encontra, e 'x' é a medida da distância horizontal percorrida pela bola, em metros, durante seu movimento. Desenhe o gráfico cartesiano representativo do movimento da bola durante o lançamento, assinalando a altura máxima e o ponto em que a bola retornaria ao solo, caso não batesse na rede.(fig. 2)
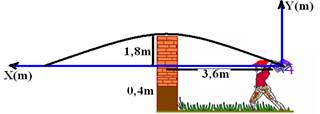
16-(UNESP-SP) Um garoto, voltando da escola, encontrou seus amigos jogando uma partida de futebol no campinho ao lado de sua casa e resolveu participar da brincadeira. Para não perder tempo, atirou sua mochila por cima do muro, para o quintal de sua casa: postou-se a uma distância de 3,6 m do muro e, pegando a mochila pelas alças, lançou-a a partir de uma altura de 0,4 m.
Para que a mochila passasse para o outro lado com segurança, foi necessário que o ponto mais alto da trajetória estivesse a 2,2 m do solo. Considere que a mochila tivesse tamanho desprezível comparado à altura do muro e que durante a trajetória não houve movimento de rotação ou perda de energia. Tomando g = 10 m/s2, calcule
a) o tempo decorrido, desde o lançamento, para a mochila atingir a altura máxima.
b) o ângulo de lançamento.
Dados:
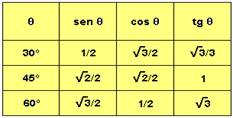
17-(UNIFESP-SP) Um projétil de massa m = 0,10 kg é lançado do solo com velocidade de 100 m/s, em um instante t = 0, em uma direção que forma 53° com a horizontal. Admita que a resistência do ar seja desprezível e adote g = 10 m/s2.
a) Utilizando um referencial cartesiano com a origem localizada no ponto de lançamento, qual a abscissa x e a ordenada y da posição desse projétil no instante t = 12 s?
Dados: sen 53° = 0,80; cos 53°= 0,60.
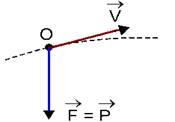
b) Utilizando este pequeno trecho da trajetória do projétil:
Desenhe no ponto O, onde está representada a velocidade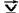 
do projétil, a força resultante 
que nele atua. Qual o módulo dessa força?
do projétil, a força resultante 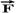que nele atua. Qual o módulo dessa força?
18- (Ufc-CE) Uma partícula pontual é lançada de um plano inclinado conforme esquematizado na figura a seguir. O plano tem um ângulo de inclinação θ em relação à horizontal, e a partícula é lançada, com velocidade de módulo v, numa direção que forma um ângulo de inclinação α em relação ao plano inclinado. Despreze qualquer efeito da resistência do ar. Considere que a aceleração da gravidade local é constante (módulo igual a g, direção vertical, sentido para baixo).
a) Considerando o eixo x na horizontal, o eixo y na vertical e a origem do sistema de coordenadas cartesianas no ponto de lançamento, determine as equações horárias das coordenadas da partícula, assumindo que o tempo é contado a partir do instante de lançamento.
b) Determine a equação da trajetória da partícula no sistema de coordenadas definido no item (a).
19-(UNESP-SP) Em uma partida de futebol, a bola é chutada a partir do solo descrevendo uma trajetória parabólica cuja altura máxima e o alcance atingido são, respectivamente, h e s.
Desprezando o efeito do atrito do ar, a rotação da bola e sabendo que o ângulo de lançamento foi de 45° em relação ao solo horizontal, calcule a razão s/h.
Dado: sen 45° = cos 45° = √2/2.
20-(UNICAMP–SP) Até os experimentos de Galileu Galilei, pensava-se que, quando um projétil era arremessado, o seu movimento devia-se ao impetus, o qual mantinha o projétil em linha reta e com velocidade constante.
Quando o impetus acabasse, o projétil cairia verticalmente até atingir o chão. Galileu demonstrou que a noção de impetus era equivocada.
Consideremos que um canhão dispara projéteis com uma velocidade inicial de 100 m/s, fazendo um ângulo de 30º com a horizontal. Dois artilheiros calcularam a trajetória de um projétil: um deles, Simplício, utilizou a noção de impetus; o outro, Salviati, as idéias de Galileu. Os dois artilheiros concordavam apenas em uma coisa: o alcance do projétil.
Considere √3 =1,8 ; sen 30º = 0,5 ; cos 30º = 0,9.
Despreze a resistência do ar.
a) Qual é o alcance do projétil?
b) Qual é a altura máxima alcançada pelo projétil, segundo os cálculos de Simplício?
c) Qual é a altura máxima alcançada pelo projétil, calculada por Salviati?
21-(PUC-PR) Um projétil de massa 100 g é lançado obliquamente a partir do solo, para o alto, numa direção que forma 60° com a horizontal com velocidade de 120 m/s, primeiro na Terra e posteriormente na Lua.
Considerando a aceleração da gravidade da Terra o sêxtuplo da gravidade lunar, e desprezíveis todos os atritos nos dois experimentos, analise as proposições a seguir:
I- A altura máxima atingida pelo projétil é maior na Lua que na Terra.
II- A velocidade do projétil, no ponto mais alto da trajetória será a mesma na Lua e na Terra.
III- O alcance horizontal máximo será maior na Lua.
IV- A velocidade com que o projétil toca o solo é a mesma na Lua e na Terra.
22-(FUVEST-SP-2008) No "salto com vara", um atleta corre segurando uma vara e, com perícia e treino, consegue projetar seu corpo por cima de uma barra. Para uma estimativa da altura alcançada nesses saltos, é possível considerar que a vara sirva apenas para converter o movimento horizontal do atleta (corrida) em movimento vertical, sem perdas ou acréscimos de energia. Na análise de um desses saltos, foi obtida a seqüência de imagens reproduzida a seguir. Nesse caso, é possível estimar que a velocidade máxima atingida pelo atleta, antes do salto, foi de, aproximadamente,
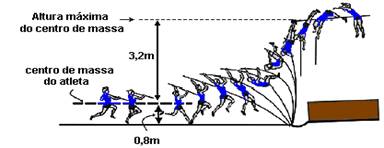
Desconsidere os efeitos do trabalho muscular após o início do salto.
a) 4 m/s b) 6 m/s c) 7 m/s d) 8 m/s e) 9 m/s
23-(Ufsm-RS-2008) Num jogo de futebol, um jogador faz um lançamento oblíquo de longa distância para o campo adversário, e o atacante desloca-se abaixo da bola, em direção ao ponto previsto para o primeiro contato dela com o solo.
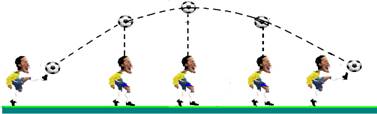
Desconsiderando o efeito do ar, analise as afirmativas:
I - Um observador que está na arquibancada lateral vê a bola executar uma trajetória parabólica.
II - O atacante desloca-se em movimento retilíneo uniformemente variado para um observador que está na arquibancada lateral.
III - O atacante observa a bola em movimento retilíneo uniformemente variado.
Está(ão) CORRETA(S)
a) apenas I. b) apenas II. c) apenas I e II. d) apenas I e III. e) apenas II e III.
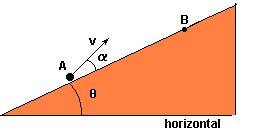
24-(FUVEST-SP-2009) O salto que conferiu a medalha de ouro a uma atleta brasileira, na Olimpíada de 2008, está representado no esquema ao lado, reconstruído a partir de fotografias múltiplas. Nessa representação, está indicada, também, em linha tracejada, a trajetória do centro de massa da atleta (CM).
Utilizando a escala estabelecida pelo comprimento do salto, de 7,04 m, é possível estimar que o centro de massa da atleta atingiu uma altura máxima de 1,25 m (acima de sua altura inicial), e que isso ocorreu a uma distância de 3,0 m, na horizontal, a partir do início do salto, como indicado na figura. Considerando essas informações, estime:
a) O intervalo de tempo t1, em s, entre o instante do início do salto e o instante em que o centro de massa da atleta atingiu sua altura máxima.
b) A velocidade horizontal média, VH, em m/s, da atleta durante o salto.
c) O intervalo de tempo t2, em s, entre o instante em que a atleta atingiu sua altura máxima e o instante final do salto.
NOTE E ADOTE: Desconsidere os efeitos da resistência do ar.
25-(ITA-SP-2009) Considere hipoteticamente duas bolas lançadas de um mesmo lugar ao mesmo tempo: a bola 1, com velocidade para cima de 30 m/s, e a bola 2, com velocidade de 50 m/s formando um ângulo de 30° com a horizontal. Considerando g = 10 m/s£, assinale a distância entre as bolas no instante em que a primeira alcança sua máxima altura.
a) d = √6250 m. b) d = √2717 m c) d = √17100 m d) d = √19375 m e) d = √26875 m
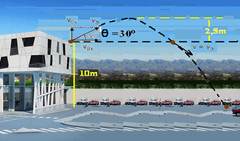
26-(UDESC-SC-2009) Em uma partida de basquete, um jogador tem direito a realizar dois lances livres. O centro da cesta está situado a uma distância de 4,0 m da linha de lançamento e a uma altura de 3,0 m do solo, conforme a figura abaixo. A bola é lançada sempre a uma altura de 2,0 m do solo.
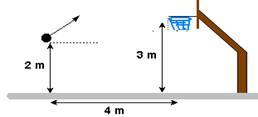
No primeiro lançamento, a bola é lançada com velocidade de 5,0 m/s, formando um ângulo de 30° com a horizontal, e não atinge a cesta. No segundo lançamento, a bola é lançada com uma velocidade desconhecida, formando um ângulo de 30° com a horizontal, e atinge a cesta.
Dados: cos 30° = 0,86; sen 30° = 0,50; tan 30° = 0,57; cos2 30° = 0,75.
a) Determine o instante em que a altura máxima é atingida pela bola no primeiro lançamento.
b) Demonstre que a bola não atinge a cesta no primeiro lançamento.
c) Determine a velocidade inicial da bola no segundo lançamento.
27-(CFT-MG-010) Uma pedra, lançada para cima a partir do topo de um edifício de 10 m de altura com velocidade inicial
vo = 10m/s, faz um ângulo de 30° com a horizontal. Ela sobe e, em seguida, desce em direção ao solo. Considerando-o como referência, é correto afirmar que a(o)
a) máxima altura atingida é igual a 15 m. b) intervalo de tempo da subida vale 3,0 s.
c) tempo gasto para chegar ao solo é 5,0 s. d) velocidade ao passar pelo nível inicial é 10m/s.
28-(PUC-RJ-010) Um superatleta de salto em distância realiza o seu salto procurando atingir o maior alcance possível. Se ele se
lança ao ar com uma velocidade cujo módulo é 10 m/s, e fazendo um ângulo de 45o em relação a horizontal, é correto afirmar que o alcance atingido pelo atleta no salto é de: (Considere g = 10 m/s2)
a) 2 m. b) 4 m. c) 6 m. d) 8 m. e) 10 m.
29-(UNIFESP-SP-010) No campeonato paulista de futebol, um famoso jogador nos presenteou com um lindo gol, no qual, ao
correr para receber um lançamento de um dos atacantes, o goleador fenomenal parou a bola no peito do pé e a chutou certeira ao gol. Analisando a jogada pela TV, verifica-se que a bola é chutada pelo armador da jogada a partir do chão com uma velocidade inicial de 20,0 m/s, fazendo um ângulo com a horizontal de 45º para cima.
Dados: g = 10,0 m/s2 e √= 1,4
a) Determine a distância horizontal percorrida pela bola entre o seu lançamento até a posição de recebimento pelo artilheiro (goleador fenomenal).
b) No instante do lançamento da bola, o artilheiro estava a 16,0 m de distância da posição em que ele estimou que a bola cairia e, ao perceber o início da jogada, corre para receber a bola. A direção do movimento do artilheiro é perpendicular à trajetória da
bola, como mostra a figura. Qual é a velocidade média, em km/h, do artilheiro, para que ele alcance a bola imediatamente antes de ela tocar o gramado?
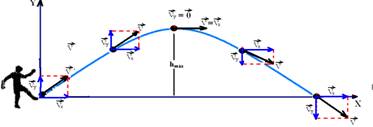
30-(UEPG-PR-011) Um projétil quando é lançado obliquamente, no vácuo, ele descreve uma trajetória parabólica. Essa trajetória é resultante de uma composição de dois movimentos independentes. Analisando a figura abaixo, que representa o movimento de um projétil lançado obliquamente, assinale o que for correto.
01) As componentes da velocidade do projétil, em qualquer instante nas direções x e y, são respectivamente dadas por,
Vx = Vo . cosθ e Vy = Vo . senθ – gt
02) As componentes do vetor posição do projétil, em qualquer instante, são dadas por,
x = Vo . cosθ. t e y = Vo . senθ – gt2/2
04) O alcance do projétil na direção horizontal depende da velocidade e do ângulo de lançamento.
08) O tempo que o projétil permanece no ar é t=(2Vosenθ)/g
16) O projétil executa simultaneamente um movimento variado na direção vertical e um movimento uniforme na direção horizontal.
(UERJ-RJ-011) Este enunciado refere-se às questões de números 31 e 32. Um trem em alta velocidade desloca-se ao
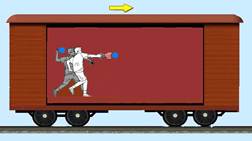
longo de um trecho retilíneo a uma velocidade constante de 108 km/h. Um passageiro em repouso arremessa horizontalmente ao piso do vagão, de uma altura de 1 m, na mesma direção e sentido do deslocamento do trem, uma bola de borracha que atinge esse piso a uma distância de 5 m do ponto de arremesso.
31-(UERJ-RJ-011) Se a bola fosse arremessada na mesma direção, mas em sentido oposto ao do deslocamento do trem,
a distância, em metros, entre o ponto em que a bola atinge o piso e o ponto de arremesso seria igual a:
(A) 0 (B) 5 (C) 10 (D) 15
32-(UERJ-RJ-011)O intervalo de tempo, em segundos, que a bola leva para atingir o piso é cerca de:
(A) 0,05 (B) 0,20 (C) 0,45 (D) 1,00
33-(UFF-RJ-011) Após um ataque frustrado do time adversário, o goleiro se prepara para lançar a bola e armar um contra ataque. Para dificultar a recuperação da defesa adversária, a bola deve chegar aos pés de um atacante no menor tempo possível. O goleiro vai chutar a bola, imprimindo sempre a mesma velocidade, e deve controlar apenas o ângulo de lançamento. A figura mostra as duas trajetórias possíveis da bola num certo momento da partida.
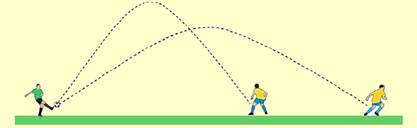
Assinale a alternativa que expressa se é possível ou não determinar qual destes dois jogadores receberia bola no menor tempo. Despreze o efeito da resistência do ar.
(A) Sim, é possível, e o jogador mais próximo receberia a bola no menor tempo.
(B) Sim, é possível, e o jogador mais distante receberia a bola no menor tempo.
(C) Os dois jogadores receberiam a bola em tempos iguais.
(D) Não, pois é necessário conhecer os valores da velocidade inicial e dos ângulos de lançamento.
(E) Não, pois é necessário conhecer o valor da velocidade inicial.
34) (UEM-PR) Um trem se move com velocidade horizontal constante. Dentro dele estão o observador A e um garoto, ambos parados em relação ao trem. Na estação, sobre a plataforma, está o observador B parado em relação a ela. Quando o trem passa pela plataforma, o garoto joga uma bola verticalmente para cima. Desprezando-se a resistência do ar, podemos afirmar que
(01) o observador A vê a bola se mover verticalmente para cima e cair nas mãos do garoto.
(02) o observador B vê a bola descrever uma parábola e cair nas mãos do garoto.
(04) os dois observadores vêem a bola se mover numa mesma trajetória.
(08) o observador B vê a bola se mover verticalmente para cima e cair atrás do garoto.
(16) o observador A vê a bola descrever uma parábola e cair atrás do garoto.
Dê como resposta a soma dos números associados às proposições corretas.
35- Um corpo tomba em queda livre desde o ponto O. Após o intervalo de tempo Dt tomba um segundo corpo do mesmo ponto O.
a) Em que instante eles estarão separados pela distância h?
b) Que distância percorreu cada um até esse instante?
c) Que valores assumirão suas respostas (a) e (b) para h = 100 m e Dt = 2
Resoluções
01- S = So + Vo.t + g.t²/2
S = 5.t² 9 (equação I)
V = Vo + g.t
8 = 0 + 10.t
t = 0,8
Substituindo t na equação I temos:
S = 5.(0,8)²
S = 5.0,64
S = 3,2m
02- Da sacada à altura máxima que o projétil alcançará.
V = Vo + g.t
0 = 10 – 10.t
10.t = 10
t = 10/10
t = 1s
0 = 10 – 10.t
10.t = 10
t = 10/10
t = 1s
Da altura máxima que o projétil alcançou ao solo.
V = Vo + g.t
30 = 0 + 10.t
10.t = 30
t = 30/10
t = 3s
30 = 0 + 10.t
10.t = 30
t = 30/10
t = 3s
O tempo em que o projétil permanece no ar:
tt = 3 + 1 = 4s
03- Se os dois ângulos de lançamento forem complementares entre si (α1 + α2=90o), e a velocidade inicial for a mesma, (no caso, 20m/so alcance horizontal é o mesmo.
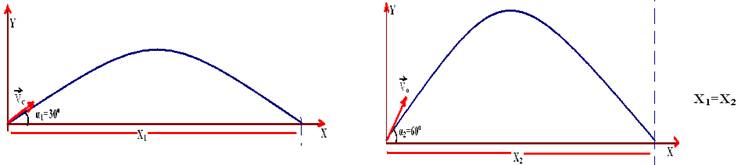
R- D
04- a) Como a resistência do ar é desprezada, a velocidade horizontal inicial do projétil é constante e, em cada instante, a mesma do caminhão. Assim, se ele partiu de um ponto P da carroceria do caminhão, retornará ao mesmo ponto P e o deslocamento horizontal em relação ao caminhão será zero.
b) Vox=20m/s --- Vo=80m/s --- Vo2=Vox2 + Voy2 --- 6.400=400 + Voy2 --- Voy=77.5m/s ---tempo de subida --- Vy = Voy – gts --- 0=77,5 – 10ts --- ts=7,75s --- tempo que demora para subir e descer e se deslocar X na horizontal --- t=2.7.75 --- t=15,5s --- X=Vox.t=20,15,5 --- X=310m
05- (01) Falsa – é o tempo de subida mais o tempo de descida
(02) Verdadeira – veja (1)
(04) Verdadeira – veja teoria - Se a altura maxima (hmáx) é igual ao alcance X --- tgα=4
(08) Ec=mV2/2 --- na altura máxima V é mínima, portanto Ec também será mínima – Falsa
(16) Falsa – como não existe atrito, o sistema é conservativo e a energia mecânica é sempre a mesma em todos os pontos da trajetória
Soma (02 + 04) = 06
06- Na altura máxima a velocidade vetorial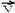 
não é nula, tem intensidade mínima e é igual à componente horizontal, ou seja, 
.
não é nula, tem intensidade mínima e é igual à componente horizontal, ou seja, .
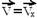Assim, Vox=20m/s --- Vox=Vocos60o --- 20=Vo.1/2 --- Vo=40m/s --- R- E
07- Na altura maxima --- hmáx=20m e t=4/2 --- t=2s --- Y=Voyt – gt2/2 --- 20=Voy.2 – 10.22/2 --- Voy=20m/s --- Y=Voyt – gt2/2 --- Y=20t – 5t2 --- R- A
08- No ponto mais alto --- V=Vx=Vox=20/2 --- Vox=10m/s --- Vo2=Vox2 + Voy2 --- 202=102 + Voy2 --- Voy2=300 --- na altura máxima hmáx --- Vy=0 --- Torricelli --- Vy2 = Voy2 – 2ghmáx --- 02=300 – 20hmáqx --- hmáx=15m
09- a) Movimento na vertical --- no ponto A de altura máxima Vy=0
S=So + Vot + at2/2 --- YB) = Y(A) + Vyt – 10t2/2 --- 4,2 = 5,0 +0.t -5t2 --- t=√0,16 --- t=0,4s
b) Queda livre da altura Yo=5m --- Vo=0 --- quando chega ao solo Y=0 --- Y=Yo + Vot –gt2/2 --- 0=5 + 0t – 5t2 --- t=1s
b) Queda livre da altura Yo=5m --- Vo=0 --- quando chega ao solo Y=0 --- Y=Yo + Vot –gt2/2 --- 0=5 + 0t – 5t2 --- t=1s
Sendo o choque elástico, o tempo de subida é igual ao tempo de descida --- t=2s
c) Movimento vertical --- a batida na parede não afeta o tempo de queda (projeção na vertical) pois o choque é elástico --- t=1s --- Voy=0 --- velocidade com que chega ao solo --- Vy --- Vy=Voy – gt --- Vy=0 -10.1 --- Vy=-10m/s --- se chega ao solo com velocidade de -10m/s, sai do mesmo com velocidade de +10m/s ---
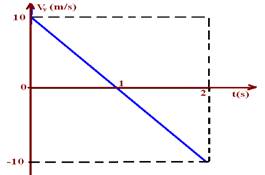
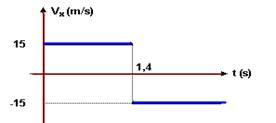
No movimento horizontal ela demora t=0,4s para percorrer X=6m com velocidade constante Vx --- X=Vxt --- 6=Vx.0,4 --- Vx=15m/s --- +15m/s para a direita (movimento progressivo) e -15m/s para a esquerda (movimento retrógrado)
10- Vox=Vocos45o --- Voy=Vosen45o --- Vox=Voy=0,7Vo --- tempo que o dardo demora para para percorrer 16m na horizontal --- X=Voxcos45o.t --- 16=Vo.0,7.t --- t=16/0,7Vo --- Na altura máxima Vy=0 e t=16/2.(0,7Vo)=16/1,4Vo --- Vy=Voy – gt --- 0=0,7Vo – 10t --- 0=0,7Vo – 10.16/1,4Vo --- Vo=√163,2=12,8m/s --- t=16/0,7Vo --- t=16/12,8=1,8s --- R- B
11- a) A única força que age sobre a bola (a resistência do ar é desprezada) durante todo o movimento é a força peso, vertical e para
baixo.
b) Cálculo do tempo que a bola demora a chegar até o goleiro percorrendo X=40m com velocidade horizontal constante e de valor Vox=Vocos25o=26.0,91 --- Vox=23,66m/s --- X=Vox.t --- 40=23,66.t --- t=1,69s --- cálculo da altura, na direção vertical, que a bola estará ao chegar ao goleiro nesse instante (t=1,69s) --- Y=Voyt – gt2/2 --- Y=Vo.sen25o.t –gt2/2 --- Y=26.0,42.1,69 – 10.(1,69)2/2 --- Y=18,45 – 14,28 --- Y=4,17m --- esse valor é maior que 3m e assim, o goleiro não consegue tocar a bola.
c) Cálculo do tempo que a bola demora para chegar à altura vertical de 1,5m --- Y=Vo.sen25o.t – gt2/2 --- 1,5=10,92t – 5t2 ---
5t2 -10,92t + 1,5=0 --- Δ=119,25 – 30=89,25 --- √Δ=9,5 --- t=(10,92 ±9,5)/2.5 --- considera-se o tempo maior que ocorre quando a bola já está descendo --- t=2,042s --- nesse instante a distância horizontal da linha de gol será de X=Vocos25o.t ---
X=26.0,91.2,042 --- X=48,3m
12- O tempo que a gota de barro permanece no ar é o mesmo tempo que a roda demora para efetuar uma volta completa, ou seja, percorrer ΔS=2πR com velocidade constante V, que é a velocidade de translação e de rotação da roda (não derrapa) e que também é a velocidade de lançamento da gota de barro --- V= ΔS/Δt --- V=2πR/t --- t=2πR/V --- a gota de barro atinge a altura máxima hmáx na metade desse tempo, quando sua velocidade vertical Vy se anula (Vy=0) --- Vy=Voy – gt --- 0=V – g(πR/V) ---
V2=πRg --- V=√(πRg)
13- a) Do gráfico --- distância vertical que percorre até atingir a altura máxima --- ΔS=125 – 93,75=31,25cm --- ΔS=0,3125m --- na altura máxima Vy=0 --- Torricelli --- Vy2 = Voy2+ 2aΔS --- 02=Voy2 – 2.10.0,3125 --- Voy=2,5m/s --- função horária vertical --- Y=Yo + Voyt – gt2/2 --- quando chega ao solo Y=0 --- 0=0,9375 + 2,5t – 5t2 --- 5t2 – 2,5t – 0,9375=0 --- √Δ=5 ---
t=(2,5 ±5)/10 --- t=0,75s
b) Na horizontal --- quando X=24m --- t=0,75s --- X=Vox.t --- 24=Vox.0,75 --- Vox=32m/s
c) sem efeito --- a força resultante sobre a bola é seu peso --- P=mg --- a=g --- com efeito --- F=3P (para cima) e P (para baixo) --- FR=3P – P=2P=2mg --- a’=2g --- como a aceleração é proporcional à velocidade, ela também dobrará --- V’+2.32 --- V’=64m/s
14- a) Yo=0 --- quando t=0,3s --- Y=1,2m --- Y=Yo + Voyt + at2/2 --- 1,2=0 + 0,3Voy= + a.(0,3)2/2 --- 0,3Voy + 0,045a=1,2 I
quando t=0,8s --- Y=1,2m --- Y=Yo + Voyt + at2/2 --- 1,2=0 + Voy.0,8 + a(0,8)2/2 --- 0,8Voy + 0,32a = 1,2 II --- resolvendo o sistema composto por I e II --- a=-10m/s2=g e Voy=5,5m/s --- tempo que demora para atingir a altura máxima onde Vy=0 --- Vy=Voy + at --- 0=5,5 – 10t --- t=0,55s --- Ymáx= Yo + Voyt + at2/2 --- Ymáx= 0 + 5,5.0,55 – 10(0,55)2/2 --- Ymáx=1,5125m
b) tempo total de movimento t=2.0,55 --- t=1,1s --- na horizontal --- X=Vox.t --- 1,3=Vox.1,1 --- Vox=1,18m/s
c) Vo2=Vox2 + Voy2 --- Vo2 = (1,18)2 + ((5,5)2 --- Vo2=1,3924 + 37,91 --- Vo=6m/s
15- a) Vo=72km/h/3,6=20m/s --- Voy=Vosen20o=20.0,35 --- Voy=7m/s --- Vox=Vocos20o=20.0,95 --- Vox=19m/s --- tempo que a bola demora para chegar à barreira onde X=9,5m com velocidade constante Vox=19m/s --- X=Vox.t --- t=9,5/19 --- t=0,5s --- nesse instante a barreira deverá ter uma altura vertical de --- Y=Voyt – gt2/2=7.0,5 – 5.0,25 --- Y=3,5 – 1,25 --- Y=2,25m
b) Tempo que a bola demora para chegar ao gol com velocidade de Vox=19m/s e distante X=19m do ponto de lançamento --- X=Voxt --- t=19/19 --- t=1s --- nesse instante a bola terá uma altura vertical de Y=Voyt – gt2/2=7.1 – 5.1 --- Y=2m (altura da bola ao entrar no gol) --- altura da trave=2,4m --- a bola entra no gol 0,4m abaixo da trave.
c) Tempo que a bola demora para atingir a altura máxima onde Vy=0 --- Vy=Voy – gt --- 0=7 – 10t --- t=0,7s --- nesse instante --- X=Voxt=19.0,7 --- X=13,3m --- Y=hmáx=V0yt – gt2/2=7.0,7 – 5.0,49=4,9 – 2,45 --- hmáx= 2,45m --- o tempo que ela
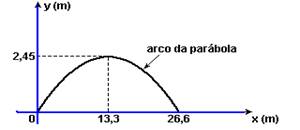
demora para retornar ao solo é o dobro do tempo que demora para atingir hmáx --- t=2.13,3 --- t=26,6s
16- a) Colocando o referencial no ponto de lançamento e aplicando Torricelli no ponto de altura máxima onde vy=0 e h=1,8m ---
V2=Voy2 – 2gh --- 02=(Vosenβ)2 -2.10.1,8 --- Vosenβ=√36 --- Vosenβ=6 --- tempo que demora para atingir hmáx --- Vy = Voy – gt --- 0=Vosenβ – 10t --- 0=6 – 10t --- t=0,6s
b) eixo vertical --- Vosenβ=6 --- senβ=Vo/6 --- eixo horizontal --- quando t=0,6s --- X=3,6m --- X=Voxt --- 3,6=Vocosβ.0,6 --- Vocosβ=6 --- cosβ=Vo/6 --- tgβ=senβ/cosβ=Vo/6 x 6/Vo --- tgβ=1 --- β=45o
17- a) Vox=Vocos53o=100.0,60 --- Vox=60m/s --- Voy=Vosen53o=100.0,80 --- Voy=80m/s --- quando t=12s --- X=Voxt=60.12 --- X=720m --- Y=Voyt – gt2/2=80.12 – 5.(12)2=960 - 720 --- Y=240m
b) A força resultante é o peso do projétil, de direção vertical e sentido para baixo e de intensidade P=mg=0,1.10 --- P=1,0N
18- a) Observe a figura abaixo, onde você deve decompor V em suas componentes vertical Vy e horizontal Vx
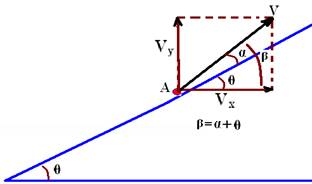
Vx=Vcosβ --- Vx=Vcos(α + θ) --- Vy=Vsenβ --- Vy=Vsen(α + θ) --- equação horária segundo a horizontal X --- X=Voxt=Vxt --- X=V.cos (α + θ).t --- Y=Vyt – gt2/2 --- Y=Vsen (α + θ).t – gt2/2
b) Isolando t em X=Vcos(α + θ)t --- t=X/Vcos(α + θ) que, substituída em Y=Vsen(α + θ)t – gt2/2 --- Y=Vsen(α + θ).X/Vcos(α + θ) – g(X/Vcos(α + θ))2/2 --- Y=tg(α + θ) – g.X2/2V2cos2(α + θ)
19- Voy=Vosen45o --- Voy=√2/2Vo --- Vox=Vocos45o --- Vox=√2/2Vo --- cálculo do tempo de subida que ocorre na altura máxima quando Vy=0 --- Vy=Voy – gt --- 0=√2/2Vo – gt --- t=√2.Vo/2g (tempo de subida) --- na horizontal --- X=s=Vox2t --- s=√2/2.Vo2(√2Vo/2g) --- s=Vo2/g --- na vertical --- Y=h==Voyt – gt2/2=√2/2.Vo(√2.Vo/2g) – g.(√2Vo/2g)2/2 --- h=Vo2/2g – Vo2/4g --- h=Vo2/4g --- s/h=Vo2/g x 4g/Vo2 --- s/h=4
20- a) Vox=Vocos30o=100.0,9=90m/s --- Voy=Vosen30o=100.0,5=50m/s --- tempo para atingir hmáx o que ocorre quando Vy=0 ---
Vy=Voy – gt --- 0=50 – 10t --- t=5s --- o alcance ocorre em t=2.5 --- t=10s --- X=Voxt=90.10 --- X=900m
b) hmáx segundo Simplício ---
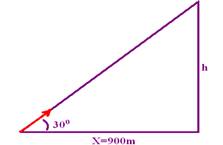
tg30o=h/900 --- √3/3=h/900 --- 1,8/3=h/900 --- h=540m
c) hmáx segundo Salviati --- Voyt – gt2/2=50.5 – 5.25/2=250 - 125 --- hmáx=125m
21- I- Voy é a mesma (mesmo V0 e o mesmo ângulo) --- Na hmáx --- Vy=0 --- Vy2 = Voy2– 2.g.hmáx --- 0 = Voy2 – 2ghmáx --- hmáx=Voy2/2g --- se g diminui, hmáx aumenta --- Verdadeira
II – Correta --- a velocidade do projétil no aponto mais alto da trajetória é nula na Terra e na Lua.
III – Vox é a mesma --- X=Vox.t --- o alcance horizontal X independe de g, assim X é o mesmo na Terra e na Lua.
IV – Correta --- a velocidade vertical com que ele é lançado é a mesma, veja I, quem varia é g.
22- Na altura máxima --- Vy=0 e h=3,2m --- Torricelli --- Vy2=Voy2 – 2gh --- 02=Voy2 – 2.10 3,2 --- Voy=8m/s --- R- D
23- I – Verdadeira --- vê uma composição de dois movimentos, um na vertical e outro na horizontal.
II – Falsa --- desloca-se em movimento retilíneo uniforme com velocidade horizontal constante.
III – Correta – na vertical o movimento é uniformemente variado com aceleração a=-g.
R- D
24- a) Na hmáx --- Vy=0 --- hmáx=1,25m --- Torricelli --- Vy2=Voy2 – 2ghmáx --- 02 = Voy2 -20.1,25 --- Voy=5m/s --- Vy=Voy – gt --- 0=5 – 10t --- t1=0,5s
b) X=Voxt=Vox2t1 --- 6=Vox.1 --- Vox=6,0m/s
c) Trata-se do tempo que ele demora para percorrer na horizontal, com velocidade de Vox=6ms a distância X=(7,04 – 3,0)=4,04m --- X=Voxt2= --- 4,04=6t2 --- t2=0,67s
25- Bola 1 --- lançamento vertical --- tempo para atingir hmáx onde V=0 --- V=Vo – gt --- 0=30 – 10t --- t=3s --- hmáx= 30.3 – 5.9 --- hmax= 45m
Bola 2 --- lançamento oblíquo --- quando t=3s --- h’=Voyt – gt2/2 --- h’=Vosen30o.t – gt2/2=50.1/2.3 – 10.9/2=75 – 45 --- -- h’=30m --- X=Vocos30o.t=50.√3/2.3 --- X=127,5m --- a distância pedida é d, conforme figura abaixo
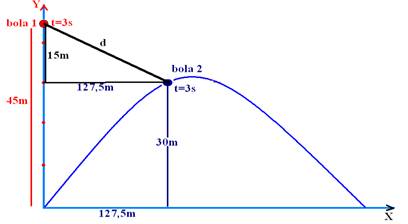
d2=(15)2 + (127,5)2 --- d=√225 + 16.256,25 --- d=√16.481,25 m --- R- D
26- a) Vy=Vosen30o – gt --- 0=5.0,5 – 10t --- t=0,25s
b) Cálculo da altura máxima --- Y=hmáx=Yo + Vocos30o – gt2/2=2 + 0,625 - 0,3125 --- hmáx=2,3125m que é menor que a altura da cesta
c) na horizontal --- X=Vocos30ot --- 4=Vo.0,86t --- t=4,6/Vo --- na vertical --- Y=Yo + Vosen30ot – gt2/2 --- 3=2 + 0,5Vo.(4,6/Vo) – 5(4,6/Vo)2 --- 1,3=106/Vo2 --- Vo=9,02m/s
27- Dados: vo = 10 m/s; ho = 10 m; q = 30° --- as componentes horizontal (vox) e vertical (voy) da velocidade inicial são ---
Vox = vo cos 30° = 10 (0,87) = 8,7 m/s --- voy = vo sem 30° = 10 (0,5) = 5 m/s.
Verificando cada uma das opções:
a) Altura máxima atingida em relação ao ponto de lançamento --- Vy2=Voy2 – 2gh --- 02= Voy2 – 2gh --- h=Voz2g=52/10 ---
h=2,5m --- em relação ao solo --- H=2,5 + 10 --- H=12,5m
b) Tempo de subida --- Vy=Voy – gt --- 0=5 – 10t --- t=0,5s
c) Com referencial no solo e orientando a trajetória para cima, o tempo para chegar ao solo é calculado pela função horária do espaço --- h=ho + Voyt – gt2/2 --- h=10 + 5t – 5t2 --- quando chega ao solo h=0 --- 0=10 + 5t – 5t2 --- t2 – t – 5=0 --- resolvendo a equação --- t @ 2,8 s.
d) Correta. Ao passar novamente pela mesma altura a pedra possui a mesma energia potencial inicial --- considerando o sistema
conservativo, então a pedra tem também a mesma energia cinética, portanto a mesma velocidade, em módulo, ou seja, se ela é lançada com velocidade de 10m/s, ao retornar passará por esse mesmo ponto com velocidade de -10m/s.
R- D
28- Dados --- vo = 10 m/s; q = 45°; g = 10 m/s2.
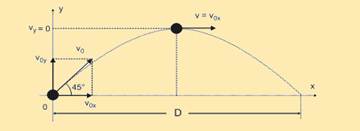
Vox = vo cos 45° = 10.√2/2 --- Vox=5√2m/s --- voy = vo sen 45° = 5√2m/s --- no eixo y o movimento é uniformemente variado, com a = –g --- tempo de subida (tsub), notando que no ponto mais alto vy = 0 --- vy = voy – g t --- 0 = 5√2 – 10 tsub ---
Tsub =√2/2 s --- tempo de subida é igual ao de descida --- tempo total (tt) --- tt=2tsub --- tt=√2s --- no eixo x o movimento é uniforme, com velocidade igual a vox --- alcance horizontal (D) --- D = vox tt = 5.√2.√2 --- D=10m --- R- E
29- Dados: g = 10 m/s2; √2= 1,4; q = 45°; vo = 20 m/s.
a) Considere desprezível a resistência do ar e que, ao matar a bola, o pé do artilheiro esteja bem próximo ao chão --- então você pode considerar o ponto de lançamento e o ponto de chegada pertencente a um mesmo plano horizontal --- no ponto mais alto a componente vertical da velocidade (vy) é nula --- vy = voy – g t Þ 0 = vosen q – g ts --- 0=20.sen45o – 10ts --- ts=20.√2/2/10 --
ts=√2 s --- tempo total =tsubida + tdescida --- ttotal= √2 + √2 --- ttotal=2√2 s --- na horizontal o movimento é uniforme --- velocidade Vx (constante) --- vx = vo cos q = vo cos 45° = 20.√2/2 m/s --- Vx=10√2 m/s --- alcance horizontal --- x=Vx.t=(10√2).(2.√2) --- x=40m
b) A velocidade média (vm) do artilheiro pode ser calculada considerando que ele percorreu a distância (DS) de 16 m enquanto a bola esteve no ar --- Vm=ΔS/Δt=16/2√2 --- Vm=4√2=4.1,4 --- Vm=5,6m/s=20,16km/h
30- Analisando apenas a incorreta, que é a 02 --- a componente horizontal está correta, pois no eixo x o movimento é uniforme, porém, no eixo y, o movimento é uniformemente variado e a equação correta é --- y = yo + voy t – gt2/2 --- yo=0 --- Voy=
Vo senθ --- Y=(Vosenθ)t – gt2/2
R- (01 + 04 + 08 + 16)=29
31- Para um observador no interior do trem que se desloca em movimento retilíneo e uniforme, o alcance de um objeto lançado horizontalmente só depende da intensidade da velocidade do objeto --- assim, caso a bola fosse arremessada em sentido oposto ao do deslocamento do trem, a distância entre o ponto de arremesso e o ponto de impacto também seria igual a 5 m --- não haveria diferença, pois a queda só é influenciada por g --- logo, seria 5m ao contrário da origem --- R- B
32- O tempo de queda é calculado exclusivamente pelo movimento vertical (queda livre da altura de 1m com a=g=10m/s2 --- h=gt2/2 --- 1=10t2/2 --- t=√0,2 --- t=0,447s --- R- C
33- O tempo de subida é igual ao tempo de descida o que ocorre quando Vy=0 --- Vy=Voy – gt --- 0=Vosenθ – gt --- t=Vosenθ/g --- tempo no ar --- ttotal=2t=2Vosenθ/g --- sendo 2Vo e g constantes, o tempo de permanência no ar depende apenas do ângulo θ com a horizontal --- quanto menor θ, menor será senθ e, consequentemente menor ttotal --- R- B
34- Para um referencial fixo no trem, a bola só tem um movimento vertical de sobe e desce, pois bola e o trem têm a mesma velocidade horizontal.
Para um referencial fixo na plataforma (na superfície terrestre), a bola tem um movimento horizontal mantido por inércia e um movimento vertical sob ação da gravidade; a composição desses dois movimentos origina uma trajetória parabólica.
(01) C
(02) C
(04) F
(08) F
(16) F
RESPOSTA: 03
na 1 questão não precisava de tantos cálculos, era só aplicar a equação de torricelli
ResponderExcluirA equação de torricelli para lançamentos para cima/baixo não seria relacionado com altura e elevado ao quadrado?
ResponderExcluirLegal mas, modifiquem o título, há questões de lançamento oblíquo tbm!.
ResponderExcluirum corpo é lançado verticalmente para cima a partir do solo com velocidade inicial de 40 m/s. Considere que a aceleração do corpo é a aceleração da gravidade (g=10m/s2). Adotando a origem do eixo de referência no solo, e orientando a trajetória para cima, determine: e) o instante em que o corpo atinge o solo f) a velocidade do corpo ao atingir o solo
ResponderExcluir