Definição de movimento uniforme
A tartaruga é um bicho estranho. Pode o mundo cair ao seu redor que ela continua se movimentando sem alterar a sua velocidade. Depois que ela sai do repouso e entra em movimento, ela dificilmente varia sua velocidade (fig. 2.1).
A tartaruga anda em cada segundo a distância de 10 cm, percorrendo distâncias iguais em tempos iguais (fig. 2.1), indicando que a velocidade da tartaruga é constante.
O movimento é uniforme quando a velocidade escalar do móvel é constante em qualquer instante ou intervalo de tempo, significando que, no movimento uniforme o móvel percorre distâncias iguais em tempos iguais.
O movimento é retilíneo uniforme quando o móvel percorre uma trajetória retilínea e apresenta velocidade escalar constante.
O movimento da tartaruga é um exemplo de movimento uniforme.
Como a velocidade escalar é constante em qualquer instante ou intervalo de tempo no movimento uniforme, a velocidade escalar média é igual à instantânea:
V = Vinst = Vmédia =  S/t | (1.1) |
Movimento retilíneo uniforme (MRU)
O movimento é retilíneo uniforme quando o móvel percorre uma trajetória retilínea e apresenta velocidade escalar constante.
Considerando que o PUCK realizou a seguinte trajetória:
O PUCK percorreu em um intervalo de tempo t = 0,1 s a distância S = 3,0 cm (fig. 1.2).
t = 0,1 s a distância S = 3,0 cm (fig. 1.2).
Observe que a trajetória é uma reta e o PUCK percorre distâncias iguais em tempos iguais, o que indica que a velocidade escalar é constante.
Calculando a velocidade no intervalo de tempo considerado, tem-se que:
V = S/t = 3,0/0,1 = 30,0 cm/s
S/t = 3,0/0,1 = 30,0 cm/s
Considerando-se quaisquer outros intervalos de tempo ou instantes, a velocidade será sempre de 30,0 cm/s.
Conclui-se que o movimento do PUCK neste exemplo é um movimento retilíneo uniforme.
Equação horária do Movimento Uniforme
A equação horária de um movimento mostra como o espaço varia com o tempo: S = f(t)
No movimento uniforme temos que:
V = Vmédia = Vinst = S/t = (S - S0)/(t - t0) |
De (1.1), obtemos:
S - S0 = V (t - t0)
Para t0 = 0
S - S0 = V. tResolvendo para S:
| S = S0 + V. t Função horária do Movimento Uniforme |
onde:
- S: espaço finalS0: espaço inicial
t: instante final
Essa é uma função do primeiro grau e é chamada de função horária da posição. Através dela podemos determinar a posição de um móvel num determinado instante.
GRÁFICOS DO MOVIMENTO UNIFORME
No movimento uniforme, os gráficos mais usados são o de velocidade em função do tempo e o do espaço em função do tempo. Vimos que o movimento uniforme é caracterizado por um movimento com velocidade constante. Por isso, o gráfico será representado por uma reta paralela ao eixo do tempo. Se a reta estiver acima do eixo do tempo, o movimento será progressivo. Se estiver abaixo do eixo do tempo, o movimento será retrógrado.
Uma propriedade importante de todo gráfico de velocidade em função do tempo é que se calcularmos a área entre a curva do gráfico delimitada por um determinado intervalo de tempo e o eixo do tempo, essa área será numericamente igual ao deslocamento do móvel.
.
Gráfico do espaço em função do tempo
Vimos que a relação entre espaço e tempo em um movimento uniforme é dada pela equação
O ponto de partida da reta indica o espaço inicial do móvel e, se a reta tem inclinação para cima, a velocidade é positiva e o movimento é progressivo. Já se a reta tiver inclinação para baixo, a velocidade é negativa e o movimento é retrógrado.
Movimento Uniformemente variado (MUV)
Também conhecido como movimento acelerado, consiste em um movimento onde há variação de velocidade, ou seja, o móvel sofre aceleração à medida que o tempo passa.
Mas se essa variação de velocidade for sempre igual em intervalos de tempo iguais, então dizemos que este é um Movimento Uniformemente Variado (também chamado de Movimento Uniformemente Acelerado), ou seja, que tem aceleração constante e diferente de zero.
O conceito físico de aceleração, difere um pouco do conceito que se tem no cotidiano. Na física, acelerar significa basicamente mudar de velocidade, tanto tornando-a maior, como também menor. Já no cotidiano, quando pensamos em acelerar algo, estamos nos referindo a um aumento na velocidade.
O conceito formal de aceleração é: a taxa de variação de velocidade numa unidade de tempo, então como unidade teremos:
Aceleração média
Assim como para a velocidade, podemos definir uma aceleração média se considerarmos a variação de velocidade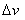 
em um intervalo de tempo 
, e esta média será dada pela razão:
em um intervalo de tempo 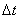, e esta média será dada pela razão:
Suas unidades são: cm/s2, m/s2, km/h2, etc.
Graficamente:
 |
ou
|  |
Velocidade em função do tempo
No entanto, quando este intervalo de tempo for infinitamente pequeno, ou seja,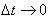 
, tem-se a aceleração instantânea do móvel.
, tem-se a aceleração instantânea do móvel.
Isolando-se o :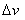
:
Mas sabemos que:
Então:
Entretanto, se considerarmos 
, teremos a função horária da velocidade do Movimento Uniformemente Variado, que descreve a velocidade em função do tempo [v=f(t)]:
, teremos a função horária da velocidade do Movimento Uniformemente Variado, que descreve a velocidade em função do tempo [v=f(t)]:
Movimento acelerado e retardado
Movimento acelerado: tomemos como exemplo a função v=15+2t. Sabemos que sua velocidade inicial é v0=15m/s e a aceleração constante do movimento é igual a 2m/s2, podemos perceber que qualquer valor para t positivo ou igual a 0 (t≥0)a velocidade sempre será positiva,logo o movimento é acelerado.
Movimento retardado: tomemos como exemplo a função v=-6+2t. Sabemos que sua velocidade inicial é vo=-6m/s e sua aceleração constante é a=2m/s2,podemos perceber que para 0≤ t<3 o movimento é retardado, e para t=3 a velocidade do móvel se anula, assim sendo para t>3 o móvel muda de sentido passa de retardado para acelerado.
Exemplo:
A velocidade de uma partícula varia de acordo com a função v=4+8t.Pede-se
- a) A velocidade inicial da partícula
- b) A aceleração da partícula
- c) A velocidade da partícula no instante t=2s
- d) A variação de velocidade nos 4 primeiros segundos
Resolução
a) Como V=vo+at ,temos v=4+8t ,então vo=4m/s
b) Sua aceleração é constante característica do MRUV,a=8m/s2
c) V=4+8.2=20m/s
d) V4= 4+8.4=36m/s ; Então ΔV= V4-V0=36-4=32m/s
Função Horária do MRUV
Sabendo-se que a aceleração no MRUV permanece constante podemos calcular a variação do espaço de um móvel no decorrer do tempo.
S=So+Vot+at2/2
A fórmula acima constitui uma função quadrática (2º grau).
Vejamos um exemplo:
Determine a velocidade inicial o espaço inicial e a aceleração do móvel uma vez que o mesmo encontra-se em MRUV seguindo a função S=20-2t+t2
Resolução:
Como S=So+Vot+at2/2,temos
So=20m
V0=-2m/s
a= 1×2=2m/s2
No gráfico Vxt, a inclinação é a aceleração
Pra descobrir o deslocamento, o papo é o mesmo do MU: área debaixo da curva. O único complicador é que agora não vai ser área do retângulo. Pode aparecer área do triângulo para um móvel partindo do repouso ou área do trapézio para um móvel com velocidade inicial não-nula.
Aceleração por tempo (axt)
O gráfico aceleração por tempo por sua vez deve ser uma função constante, lembrando que a aceleração é constante no MUV, e assim, o gráfico ficará paralelo ao eixo do tempo:
Propriedades do M.U.V.
P1 - No M.U.V., a função horária dos espaços é do 2º grau em t e é dada por: s = so + vo.t + a/2 t2.
P2 - No M.U.V., a função horária da velocidade escalar é do 1° grau em t e é dada por: v = vo + at.
P3 - A equação de Torricelli traduz a velocidade escalar em função dos deslocamentos e é dada por: v2 = vo2 + 2aDs.
P4 - No M.U.V., a aceleração escalar instantânea é constante e diferente de zero, sendo, portanto, igual à aceleração média.
P5 - No M.U.V., para intervalos de tempos iguais, o móvel sofre iguais variações em sua velocidade escalar.
P6 - No M.U.V., a velocidade escalar média pode ser dada através do já conhecido quociente Ds/Dt, ou também, através da média aritmética entre as velocidades escalares final e inicial.
P5 - No M.U.V., para intervalos de tempos iguais, o móvel sofre iguais variações em sua velocidade escalar.
P6 - No M.U.V., a velocidade escalar média pode ser dada através do já conhecido quociente Ds/Dt, ou também, através da média aritmética entre as velocidades escalares final e inicial.
Gráficos do Movimento Uniformemente Variado (M.U.V)
- Posição por tempo (Sxt)
No MUV o gráfico posição por tempo corresponde à função horária deste tipo de movimento, da forma S(t) = S₀ + V₀.t + (a.t²)/2, e sendo assim deve mostrar 0 gráfico de uma função quadrática, afinal tem t².
No movimento uniforme a inclinação do gráfico Sxt da a informação da velocidade, no MUV isto também é verdade, mas a trigonometria mais básica não nos ajuda a descobrir a velocidade neste caso. É preciso de um pouco mais de matemática. O que não quer dizer que não nos dê nenhuma informação.
Lembra que no MUV a personagem principal é a aceleração? Então, se a aceleração é positiva, isso significa que a velocidade aumenta e se negativa, significa que a velocidade diminui. Repare, nográfico anterior, que a parábola decresce ao invés de aumentar para a<0, ou seja, sua inclinação vai diminuindo.
- Velocidade por tempo (Vxt)
No MUV, o gráfico que mais nos dá informações é o gráfico Vxt. Como vimos no MU, a área debaixo do gráfico é capaz de nos dizer o deslocamento, isso também vale no MUV. Contudo como a velocidade passa a ser, também uma função horária, v(t) = v₀ + a.t, o gráfico não será paralelo ao eixo do tempo e terá a cara de uma reta com inclinação.
Um detalhe importante é notar a direção do gráfico, pois o sinal da aceleração influencia.
Outra funcionalidade do gráfico Vxt, é descobrir o móduloaceleração, vamos lá:
Veja que similarmente ao que fizemos no gráfico Sxt do MU, vamos extrair a tangente daquele trianglinho cor de “burro-quando-foge” do gráfico.
Tgθ = ΔV/Δt
Ou seja, como:
a = ΔV/Δt
Tgθ = a
No gráfico Vxt, a inclinação é a aceleração
Pra descobrir o deslocamento, o papo é o mesmo do MU: área debaixo da curva. O único complicador é que agora não vai ser área do retângulo. Pode aparecer área do triângulo para um móvel partindo do repouso ou área do trapézio para um móvel com velocidade inicial não-nula.
Aceleração por tempo (axt)
O gráfico aceleração por tempo por sua vez deve ser uma função constante, lembrando que a aceleração é constante no MUV, e assim, o gráfico ficará paralelo ao eixo do tempo:
E qual informação podemos extrair do gráfico axt? Bem, podemos tentar calcular a área debaixo da curva e ver no que dá:
A área em questão é a do retângulo formado no intervalo de tempo Δt = t2 – t1, pela área do retângulo temos:
Área = base x altura
Área = (t2 – t1).(a-0)
Área = Δt.a (1)
Entretando, pela definição de aceleração temos que:
a = ΔV/Δt
multiplicando cruzado tempos que
ΔV = Δt.a (2)
Substituindo (1) em (2), temos
Área = ΔV
No gráfico axt a área debaixo da curva é a variação da velocidade
Até a próxima!
Equação de Torricelli
Se substituirmos a equação V=vo+at na equação S=So+Vot+at2/2, teremos a equação de Torricelli
V2=v02+2αΔs
Exemplo:
Um determinado veiculo em certo instante, possui uma velocidade de 20m/s. A partir deste instante o condutor do veiculo acelera seu carro constantemente em 4m/s2.Qual a velocidade que o automóvel terá após ter percorrido 130m.
Resolução:
Aplicando a equação de Torricelli, temos
V2=v02+2αΔs
V2=202+2.4.130
V2=400+1040
V2=1440
V=38m/s
Fonte: http://educar.sc.usp.br/
Questões resolvidas sobre movimento uniforme e movimento uniformemente variado
1) (FGV-SP) - Os espaços de um móvel em função do tempo são dados por:
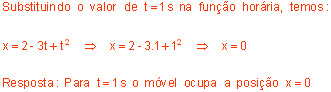
1) (FGV-SP) - Os espaços de um móvel em função do tempo são dados por:
x = 2 - 3 t + t2
onde x representa o espaço medido em metros, com relação a um certo referencial; e t, o instante medido em segundos. Calcule o espaço no instante t = 1s.
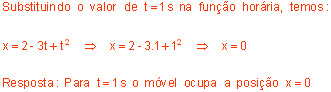
2) (UFPE) Uma bala que se move a uma velocidade escalar de 200m/s, ao penetrar em um bloco de madeira fixo sobre um muro, é desacelerada até parar. Qual o tempo que a bala levou em movimento dentro do bloco, se a distância total percorrida em seu interior foi igual a 10cm?
Apesar de o problema pedir o tempo que a bala levou, para qualquer uma das funções horárias, precisamos ter a aceleração, para calculá-la usa-se a Equação de Torricelli.
Observe que as unidades foram passadas para o SI (10cm=0,1m)
A partir daí, é possível calcular o tempo gasto:
3) (FUVEST) - Um veículo parte do repouso, em trajetória retilínea, com aceleração escalar constante e igual a 2,0 m/s2. Após 3,0 s de movimento, calcule:
a) a distância percorrida;
b) a velocidade escalar adquirida.
4) (ESPM-SP) - Se o espaço de um móvel em função do tempo é dado por s = 3 + 8 t - 2 t2 (s" m; t " s), determine o valor da velocidade quando t = 4s.
5) FM ABC-SP) - A função horária do movimento de uma partícula é expressa por s = t2 - 10 t + 24 (SI). Qual a posição do móvel ao mudar de sentido?
6) (FUVEST) - Um ciclista A inicia uma corrida a partir do repouso, acelerando 0,50 m/s2. Nesse instante passa por ele um outro ciclista B, com velocidade constante de 5,0 m/s no mesmo sentido que o ciclista A.
a) Depois de quanto tempo após a largada o ciclista A alcança o ciclista B?
b) Que distância A percorreu até o instante de encontro com B?
7) Dois carros A e B encontram-se sobre uma mesma pista retilínea com velocidades constantes no qual a função horária das posições de ambos para um mesmo instante são dadas a seguir: xA = 200 + 20.t e xB = 100 + 40.t. Com base nessas informações, responda as questões abaixo. (M.U)
8) Um móvel com velocidade constante percorre uma trajetória retilínea à qual se fixou um eixo de coordenadas. Sabe-se que no instante t0 = 0, a posição do móvel é x0 = 500m e, no instante t = 20s, a posição é x = 200m. Determine: (M.U)
a. A velocidade do móvel.
b. A função da posição.
c. A posição nos instantes t = 1s e t = 15s.
d. O instante em que ele passa pela origem.
Solução:
.gif)
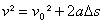
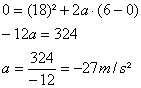
(B) 625
(C) 650
(D) 675
(E) 700
Solução:
- movimento acelerado
v² = v0² + 2aΔS
10² = 0² + 2.1.ΔS
100 = 2ΔS
ΔS = 100/2
ΔS = 50 m
- movimento uniforme
ΔS = v.t = 10.60 = 600
- movimento desacelerado
v² = v0² - 2aΔS
0² = 10² - 2 . 2 . ΔS
0 = 100 - 4ΔS
4ΔS = 100
ΔS = 100/4
ΔS = 25 m
ΔStotal = 50 + 600 + 25 = 675 m
a) É possível que o móvel A ultrapasse o móvel B? Justifique.
b). Determine o instante em que o móvel A alcançará o móvel B, caso este alcance aconteça.
b). Determine o instante em que o móvel A alcançará o móvel B, caso este alcance aconteça.
Solução:
a) Sim, pois a posição do móvel A é anterior a de B, e A possui uma velocidade constante maior que a de B; estando eles em uma mesma trajetória retilínea dentro de um intervalo de tempo Δt, A irá passar B.
b) xA = xB
200 + 20.t = 100 + 40.t
40.t - 20.t = 200 - 100
20.t = 100
t = 100/20
t = 5s
200 + 20.t = 100 + 40.t
40.t - 20.t = 200 - 100
20.t = 100
t = 100/20
t = 5s
a. A velocidade do móvel.
b. A função da posição.
c. A posição nos instantes t = 1s e t = 15s.
d. O instante em que ele passa pela origem.
Solução:
a) A velocidade do móvel
v = Δs/Δt
v = (200-500)/(20-0)
v = -300/20
v = -150m/s (velocidade negativa implica em movimento retrógrado)
v = Δs/Δt
v = (200-500)/(20-0)
v = -300/20
v = -150m/s (velocidade negativa implica em movimento retrógrado)
b) A função da posição
x = x0 + v.t
x = 500 - 15t
x = x0 + v.t
x = 500 - 15t
c) A posição nos instantes t = 1s e t = 15s
Para t = 1s temos:
x = 500 - 15.1
x = 500 – 15
x = 485m
x = 500 - 15.1
x = 500 – 15
x = 485m
Para t = 15s temos:
x = 500 – 15.15
x = 500 – 225
x = 275m
x = 500 – 15.15
x = 500 – 225
x = 275m
d) O instante em que ele passa pela origem
para x = 0 temos que:
0 = 500 – 15.t
15.t = 500
t = 500/15
t = 33,3 s em valor aproximado.
0 = 500 – 15.t
15.t = 500
t = 500/15
t = 33,3 s em valor aproximado.
9) O gráfico a seguir representa a função horária do espaço de um móvel em trajetória retilínea e em movimento uniforme.
Com base nele, determine a velocidade e a função horária do espaço deste móvel.
Solução:
v = Δs/Δt
v = (250 – 50)/(10 - 0)
v = 200/10
v = 20m/s – velocidade
v = (250 – 50)/(10 - 0)
v = 200/10
v = 20m/s – velocidade
x = xo+ v.t
x = 50 + 20.t
x = 50 + 20.t
10) Um automóvel encontra-se parado diante de um semáforo. Logo quando o sinal abre, ele arranca com aceleração 5m/s², enquanto isso, um caminhão passa por ele com velocidade constante igual a 10m/s.
(a) Depois de quanto tempo o carro alcança o caminhão?
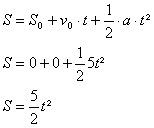
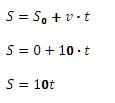
Quando os dois se encontram, suas posições são iguais, então:
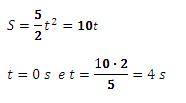
(b) Sabendo o momento do encontro, só é necessário aplicá-lo em uma das duas funções (do caminhão ou do carro).
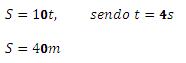
Logo o carro encontra o caminhão 4 segundos após a sinaleira abrir, a uma distância de 40 m.
(a) Depois de quanto tempo o carro alcança o caminhão?
(b) Qual a distância percorrida até o encontro. (M.U)
Escreve-se as equações do muv para o carro e do mu para o caminhão:
Carro:
Caminhão:
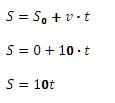
Quando os dois se encontram, suas posições são iguais, então:
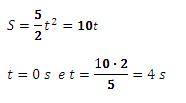
(b) Sabendo o momento do encontro, só é necessário aplicá-lo em uma das duas funções (do caminhão ou do carro).
Logo o carro encontra o caminhão 4 segundos após a sinaleira abrir, a uma distância de 40 m.
11) Um corredor chega a linha de chegada em uma corrida com velocidade igual a 18m/s. Após a chegada ele anda mais 6 metros até parar completamente. Qual o valor de sua aceleração?
12) (FCC 2011) De uma estação A, um trem de metrô parte do repouso com aceleração constante de 1,0 m/s2 até atingir 10 m/s; segue com esta velocidade por 1,0 minuto e, finalmente, freia com desaceleração constante de 2,0 m/s2, até sua chegada à estação B, onde para. A distância entre as duas estações, em m, é de (M.U)
(A) 600(B) 625
(C) 650
(D) 675
(E) 700
Solução:
- movimento acelerado
v² = v0² + 2aΔS
10² = 0² + 2.1.ΔS
100 = 2ΔS
ΔS = 100/2
ΔS = 50 m
- movimento uniforme
ΔS = v.t = 10.60 = 600
- movimento desacelerado
v² = v0² - 2aΔS
0² = 10² - 2 . 2 . ΔS
0 = 100 - 4ΔS
4ΔS = 100
ΔS = 100/4
ΔS = 25 m
ΔStotal = 50 + 600 + 25 = 675 m
13) (FFC 2003) Dois móveis percorrem uma mesma trajetória, em sentidos opostos, com movimentos uniformemente acelerados. Num determinado instante, a distância entre eles é de 630 m, os módulos de suas velocidades são 2,0 m/s e 1,0 m/s e os módulos de suas acelerações 2,0 m/s2 e 4,0 m/s2, respectivamente. A partir desse instante, a distância entre eles será de 300 m após um intervalo de tempo, em segundos, igual a (M.U)
(A) 2,0
(B) 4,0
(C) 6,0
(D) 8,0
(E)) 10
Solução
S = S0 + v0t +0,5.a.t2
S = 0 + 2t + 0,5 .2 . t2
S' = 630 - t - 0,5 .4 . t2
S' - S = 300
630 - t - 2t2 - 2t - t2 = 300
-3t2 - 3t + 330 = 0
t2 + t - 110 = 0
Δ = 1 + 440 = 441
t = (-1 + 21)/2 = 10s
(A) 2,0
(B) 4,0
(C) 6,0
(D) 8,0
(E)) 10
Solução
S = S0 + v0t +0,5.a.t2
S = 0 + 2t + 0,5 .2 . t2
S' = 630 - t - 0,5 .4 . t2
S' - S = 300
630 - t - 2t2 - 2t - t2 = 300
-3t2 - 3t + 330 = 0
t2 + t - 110 = 0
Δ = 1 + 440 = 441
t = (-1 + 21)/2 = 10s
14) (Vunesp, 2011) O gráfico das velocidades em função do tempo mostrado a seguir refere-se ao movimento de dois carros que percorrem a mesma trajetória retilínea e passam pela mesma posição em t = 0s.
Da análise desse gráfico, é correto afirmar que
(A) os carros encontram-se no instante t = 2,0 s.
(B) os carros encontram-se no instante t = 4,0 s.
(C) o carro I percorre 20 m nos primeiros 2,0 s de movimento.
(D) o carro II percorre 10 m nos primeiros 2,0 s de movimento.
(E) o carro II percorre 20 m nos primeiros 4,0 s de movimento.
Solução:
Da análise desse gráfico, é correto afirmar que
(A) os carros encontram-se no instante t = 2,0 s.
(B) os carros encontram-se no instante t = 4,0 s.
(C) o carro I percorre 20 m nos primeiros 2,0 s de movimento.
(D) o carro II percorre 10 m nos primeiros 2,0 s de movimento.
(E) o carro II percorre 20 m nos primeiros 4,0 s de movimento.
Solução:
Carro I
a = Δv/Δt = (0 - 20)/4 = - 5m/s2
S = v0.t + a.t2/2 = 20t - 5t2/2
Carro II
S = v.t = 10t
20t - 5t2/2 = 10t
- 5t2/2 + 20t - 10t = 0
5t2/2 - 10t = 0
5t2 - 20t = 0
5t(t - 4) = 0
t = 4s
(B) 45.
(C) 60.
(D) 75.
(E) 90.
Solução:
v2 = v02 + 2aΔS
0 = 152 + 2.a.20000
40000a = -225
a = -225/40000 = 0,0056
v = v0 + at
0 = 15 - 0,0056t
0,0056t = 15
t = 2678 s = 44,6 min
a = Δv/Δt = (0 - 20)/4 = - 5m/s2
S = v0.t + a.t2/2 = 20t - 5t2/2
Carro II
S = v.t = 10t
20t - 5t2/2 = 10t
- 5t2/2 + 20t - 10t = 0
5t2/2 - 10t = 0
5t2 - 20t = 0
5t(t - 4) = 0
t = 4s
15) (Vunesp, 2011) Um grande navio petroleiro com velocidade de 15 m/s percorre aproximadamente 20 km até conseguir parar. Supondo que durante a frenagem ele tenha percorrido uma trajetória retilínea com aceleração constante, pode-se afirmar que o tempo aproximado gasto nessa manobra, em minutos, é de
(A) 30.(B) 45.
(C) 60.
(D) 75.
(E) 90.
Solução:
v2 = v02 + 2aΔS
0 = 152 + 2.a.20000
40000a = -225
a = -225/40000 = 0,0056
v = v0 + at
0 = 15 - 0,0056t
0,0056t = 15
t = 2678 s = 44,6 min
16) (Fuvest 2009) Marta e Pedro combinaram encontrar-se em certo ponto de uma autoestrada plana, para seguirem viagem juntos. Marta, ao passar pelo marco zero da estrada, constatou que, mantendo uma velocidade média de 80 km/h, chegaria na hora certa ao ponto de encontro combinado. No entanto, quando ela já estava no marco do quilômetro 10, ficou sabendo que Pedro tinha se atrasado e, só então, estava passando pelo marco zero, pretendendo continuar sua viagem a uma velocidade média de 100 km/h. Mantendo essas velocidades, seria previsível que os dois amigos se encontrassem próximos a um marco da estrada com indicação de
a) km 20
b) km 30
c) km 40
d) km 50
e) km 60
17) (Uerj 2010) Um foguete persegue um avião, ambos com velocidades constantes e mesma direção. Enquanto o foguete percorre 4,0 km, o avião percorre apenas 1,0 km. Admita que, em um instante t1, a distância entre eles é de 4,0 km e que, no instante t2, o foguete alcança o avião. No intervalo de tempo t2 – t1, a distância percorrida pelo foguete, em quilômetros, corresponde aproximadamente a:
a) 4,7
b) 5,3
c) 6,2
d) 8,6
18) (Epcar 2011) Dois automóveis A e B encontram-se estacionados paralelamente ao marco zero de uma estrada. Em um dado instante, o automóvel A parte, movimentando-se com velocidade escalar constante = 80 km/h. Depois de certo intervalo de tempo, , o automóvel B parte no encalço de A com velocidade escalar constante = 100 km/h. Após 2 h de viagem, o motorista de A verifica que B se encontra 10 km atrás e conclui que o intervalo , em que o motorista B ainda permaneceu estacionado, em horas, é igual a
a) 0,25
b) 0,50
c) 1,00
d) 4,00
19) (G1 – ifsp 2012) Em um trecho retilíneo de estrada, dois veículos, A e B, mantêm velocidades constantes VA=14 m/s e VB=54 km/h Sobre os movimentos desses veículos, pode-se afirmar que:
a) ambos apresentam a mesma velocidade escalar.
b) mantidas essas velocidades, A não conseguirá ultrapassar B.
c) A está mais rápido do que B.
d) a cada segundo que passa, A fica dois metros mais distante de B.
e) depois de 40 s A terá ultrapassado B.
20) (Uespi 2012) Um motorista em seu automóvel deseja ir do ponto A ao ponto B de uma grande cidade (ver figura). O triângulo ABC é retângulo, com os catetos AC e CB de comprimentos 3 km e 4 km, respectivamente. O Departamento de Trânsito da cidade informa que as respectivas velocidades médias nos trechos AB e ACB valem 15 km/h e 21 km/h. Nessa situação, podemos concluir que o motorista:
a) chegará 20 min mais cedo se for pelo caminho direto AB.
b) chegará 10 min mais cedo se for pelo caminho direto AB.
c) gastará o mesmo tempo para ir pelo percurso AB ou pelo percurso ACB.
d) chegará 10 min mais cedo se for pelo caminho ACB.
e) chegará 20 min mais cedo se for pelo caminho ACB.
21) (Vunesp) Uma caixa de papelão vazia, transportada na carroceria de um caminhão que trafega a 90 km/h num trecho reto de uma estrada, é atravessada por uma bala perdida. A largura da caixa é de 2,00 m e a distância entre as retas perpendiculares às duas laterais perfuradas da caixa e que passam, respectivamente, pelos orifícios de entrada e saída da bala (ambas na mesma altura) é de 0,20 m. (M.U)
Supondo que a direção do disparo é perpendicular às laterais perfuradas da caixa e ao deslocamento do caminhão e que o atirador estava parado na estrada, determine a velocidade da bala, suposta constante. Resp: 250m/s (M.U)
22) (FEI-SP) Dois móveis, ambos com movimento uniforme, percorrem uma trajetória retilínea conforme mostra a figura. Em t = 0, eles se encontram, respectivamente, nos pontos A e B na trajetória. As velocidades escalares dos móveis são VA = 50 m/s e VB = 30 m/s no mesmo sentido.
Em qual ponto da trajetória ocorrerá o encontro dos móveis? (M.U)
a) 200 m
b) 225 m
c) 250 m
d) 300 m
e) 350 m
23) (ITE-SP) Dois móveis partem simultaneamente de dois pontos, A e B, e deslocam-se em movimento uniforme sobre a mesma reta, deA para B, com velocidades escalares de 20 m/s e 15 m/s. Sae o encontro ocorre 50 s após a partida, podemos afirmar que a distância inicial entre os mesmos era de: (M.U)
a) 250 m
b) 500 m
c) 750 m
d) 900m
24) Para se dirigir prudentemente, recomenda-se manter do veículo da frente uma distância mínima de um carro (4,0 m) para cada 16 km/h. Um carro segue um caminhão em uma estrada, ambos a 108 km/h.
a) De acordo com a recomendação acima, qual deveria ser a distância mínima separando os dois veículos? Resp: 27 m.
b) O carro mantém uma separação de apenas 10m quando o motorista do caminhão freia bruscamente. O motorista do carro demora 0,50 segundo para perceber a freada e pisar em seu freio. Ambos os veículos percorreriam a mesma distância até parar, após acionarem os seus freios. Mostre numericamente que a colisão é inevitável.
Resp: Durante o tempo de reação (0,50 s) o carro anda 15 m.
25) O gráfico adiante mostra como varia a velocidade de um móvel, em função do tempo, durante parte de seu movimento.
O movimento representado pelo gráfico pode ser o de uma
a) esfera que desce por um plano inclinado e continua rolando por um plano horizontal.
b) criança deslizando num escorregador de um parque infantil.
c) fruta que cai de uma árvore.
d) composição de metrô, que se aproxima de uma estação e pára.e) bala no interior de um cano de arma, logo após o disparo.
26) Um esquiador desce por uma pista de esqui com aceleração constante. Partindo do repouso do ponto P, ele chega ao ponto T, a 100 m de P, com velocidade de 30 m/s. O esquiador passa por um ponto Q, a 36 m de P, com velocidade, em m/s, de
a) 18
b) 15
c) 12
d) 10,8
e) 9,0
27) No movimento retilíneo uniformemente variado, com velocidade inicial nula, a distância percorrida é:
a) diretamente proporcional ao tempo de percurso
b) inversamente proporcional ao tempo de percurso
c) diretamente proporcional ao quadrado do tempo de percursod) inversamente proporcional ao quadrado do tempo de percurso
e) diretamente proporcional à velocidade
a) diretamente proporcional ao tempo de percurso
b) inversamente proporcional ao tempo de percurso
c) diretamente proporcional ao quadrado do tempo de percursod) inversamente proporcional ao quadrado do tempo de percurso
e) diretamente proporcional à velocidade
28) Um caminhão com velocidade de 36 km/h é freado e pára em 10 s. Qual o módulo da aceleração média do caminhão durante a freada?
a) 0,5 m/s²
b) 1,0 m/s²
c) 1,5 m/s²
d) 3,6 m/s²
e) 7,2 m/s²
29) Pode-se afirmar corretamente que
a) no intervalo de tempo de 2 s a 6 s, o deslocamento do objeto tem módulo 80 m.
b) o movimento é acelerado desde t = 0 a t = 6 s.
c) a aceleração do movimento tem módulo 7,5 m/s².
d) a aceleração é nula no instante t = 2 s.
e) nos instantes t = 0 e t = 4 s, o móvel se encontra na mesma posição.
b) o movimento é acelerado desde t = 0 a t = 6 s.
c) a aceleração do movimento tem módulo 7,5 m/s².
d) a aceleração é nula no instante t = 2 s.
e) nos instantes t = 0 e t = 4 s, o móvel se encontra na mesma posição.
30) (UNCISAL/2010) Numa avenida retilínea, um automóvel parte do repouso ao abrir o sinal de um semáforo, e atinge a velocidade de 72 km/h em 10 s. Esta velocidade é mantida constante durante 20 s, sendo que, em seguida, o motorista deve frear parando o carro em 5 s devido a um sinal vermelho no próximo semáforo.
Considerando os trechos com velocidades variáveis uniformemente, o espaço total percorrido pelo carro entre os dois semáforos é, em m,
a) 450.
b) 500.
c) 550.
d) 650.
e) 700.
31) (PUC RJ/2010) Um corredor olímpico de 100 metros rasos acelera desde a largada, com aceleração constante, até atingir a linha de chegada, por onde ele passará com velocidade instantânea de 12 m/s no instante final. Qual a sua aceleração constante?
a) 10,0 m/s²
b) 1,0 m/s²
c) 1,66 m/s²
d) 0,72 m/s²
e) 2,0 m/s²
32) (ACAFE/SC) Caracterizar o movimento de um móvel implica em compreender os conceitos de velocidade e aceleração, esses determinados a partir da variação de posição em função do tempo.
Assim, para um carro que se desloca de Joinville a Florianópolis pela BR-101, sem parar, é correto afirmar que para esse trajeto o movimento do carro é:
a) uniformemente variado, pois a aceleração do carro é constante.
b) variado, pois ocorre variação da posição do carro.
c) uniforme, pois a aceleração do carro é constante.
d) variado, pois ocorre variação da velocidade do carro.
33) (FUND. CARLOS CHAGAS) Dois móveis A e B movimentam-se ao longo do eixo x, obedecendo às equações móvel A: xA = 100 + 5,0t e móvel B: xB = 5,0t2, onde xA e xB são medidos em m e t em s. Pode-se afirmar que:
a) A e B possuem a mesma velocidade;
b) A e B possuem a mesma aceleração;
c) o movimento de B é uniforme e o de A é acelerado;
d) entre t = 0 e t = 2,0s ambos percorrem a mesma distância;
e) a aceleração de A é nula e a de B tem intensidade igual a 10 m/s2.
34) (UFMA) Uma motocicleta pode manter uma aceleração constante de intensidade 10 m/s2. A velocidade inicial de um motociclista, com esta motocicleta, que deseja percorrer uma distância de 500m, em linha reta, chegando ao final desta com uma velocidade de intensidade 100 m/s é:
a) zero
b) 5,0 m/s
c) 10 m/s
d) 15 m/s
e) 20 m/s
Nenhum comentário:
Postar um comentário