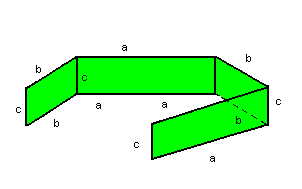
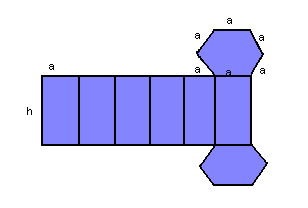
Consideremos o prisma como um sólido geométrico formado pelos seguintes elementos: base, altura, vértices, arestas e faces laterais. Os prismas podem apresentar diversas formas, mas algumas características básicas definem esse sólido geométrico. Por exemplo, o número de faces do prisma será exatamente igual ao número de lados do polígono que constitui suas bases (superior e inferior), dessa forma, sua classificação quanto ao número de lados pode ser:
Triangular – base constituída de triângulos.
Quadrangular – base constituída de quadriláteros.
Pentagonal – base constituída de pentágonos.
Hexagonal – base constituída de hexágonos.
Heptagonal – base constituída de heptágonos.
Octogonal – base constituída de octógonos.
De acordo com a inclinação das arestas laterais, um prisma pode ser classificado em:
Reto: quando as arestas laterais forem perpendiculares às arestas das bases;
Oblíquo: quando as arestas laterais não forem perpendiculares às arestas das bases.
.jpg)
Observação: em um prisma reto, as faces laterais são retangulares. Prisma regular é um prisma reto cujas bases são polígonos regulares. Vejamos alguns exemplos:

Secção
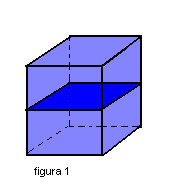
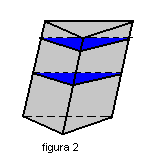
Chama-se secção de um prisma à intersecção desse prisma com um plano que intercepta todas as suas arestas laterais. Se a secção for paralela às bases, ela é chamada secção transversal (figura.1). Todas as secções transversais são congruentes ( figura 2). Se a secção for perpendicular às arestas laterais, ela é chamada secção reta.
Área lateral e área total de um prisma
Num prisma, distinguimos dois tipos de superfície:as faces e as bases. Assim, temos de considerar as seguintes áreas:
a) área de uma face (AF ):área de um dos paralelogramos que constituem as faces;
b) área lateral ( AL ):soma das áreas dos paralelogramos que formam as faces do prisma.
No prisma regular, temos:
AL = n . AF (n = número de lados do polígono da base)
c) área da base (AB): área de um dos polígonos das bases;
d) área total ( AT): soma da área lateral com a área das bases
AT = AL + 2AB
Vejamos um exemplo.
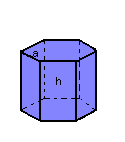
Dado um prisma hexagonal regular de aresta da base a e aresta lateral h, temos:
 |

Exemplos:
Solução:
Chamemos de n o número das suas faces.
Como duas das faces são bases, teremos (n – 2) faces laterais. Assim sendo, em cada base existirão (n – 2) arestas.
O total de arestas é dado por:
Total de arestas = arestas das bases + arestas laterais
Portanto:
2 * (n – 2) + (n – 2) = 18
Resolvendo essa equação, encontramos n = 8.
O prisma tem então 8 faces e cada base tem 8 – 2 = 6 arestas.
Portanto esse é um prisma hexagonal.
2) Quantas faces tem um prisma com 30 arestas.
2 * (n – 2) + (n + 2) = 30
2n – 4 + n – 2 =30
3n = 30 + 4 + 2
3n = 36
N = 12 faces
paralelepípedo
Paralelepípedo é um prisma que possui em suas bases um paralelogramo. Sendo que o paralelepípedo é configurado pela reunião dos seis paralelogramos que o constituem. Assim, podemos ter:
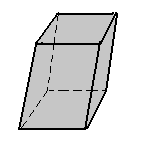
a) paralelepípedo oblíquo
 |
b) paralelepípedo reto
 |
Se o paralelepípedo reto tem bases retangulares, ele é chamado de paralelepípedo reto-retângulo,ortoedro ou paralelepípedo retângulo.
Diagonal do paralelepípedo
Considere a figura a seguir:
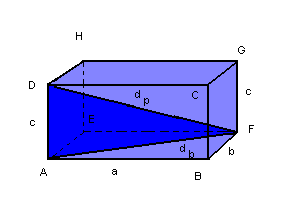 |
db = diagonal da base
dp = diagonal do paralelepípedo
|
Na base ABFE, temos:
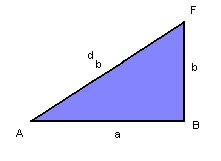 |
No triângulo AFD, temos:
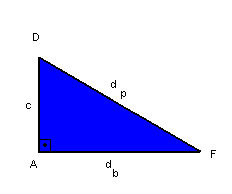 |
Exemplo:
Calcular a medida da diagonal de um paralelepípedo retângulo de dimensões 5 cm, 8 cm e 6 cm.
Solução:
d = √ a² + b² + c²
d = √ 5² + 8² + 6²
d = √ 25 + 64 + 36
d = √ 125
d = √ 5 *√ 25
d = 5√ 5
Logo, a medida da diagonal é 5√5
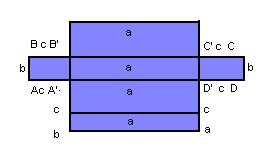
Área lateral do paralelepípedo retângulo
Sendo AL a área lateral de um paralelepípedo retângulo, temos:
AL= ac + bc + ac + bc = 2ac + 2bc =AL = 2(ac + bc)
Área total do paralelepípedo retângulo
Planificando o paralelepípedo, verificamos que a área total é a soma das áreas de cada par de faces opostas:
 Exemplo:
Calcule a área lateral e total de um paralelepípedo retângulo de dimensões a = 15 cm, b= 10 cm, c = 8 cm, sendo que a altura dele corresponde à menor das suas dimensões.
Solução:
A área lateral é dada por:
AL= 2 * (15 * 8 + 10 * 8)
AL = 2 * (120 + 80) = 400
A área lateral é 400 cm³.
A área total é dada por:
At = 2 * (15 * 10 + 15 * 8 + 10 * 8) = 2 * (150 + 120 + 80) = 700
A área total é 700 cm³.
Volume do paralelepípedo retângulo
1 m³ (metro cúbico) = 1000 L (litros) 1 dm³ (decímetro cúbico) = 1 L 1 cm³ (centímetro cúbico) = 1 mL (mililitro) Exemplo: Um aquário possui o formato de um paralelepípedo com as seguintes dimensões: .jpg) Determine quantos litros de água são necessários para encher o aquário. V = comprimento x largura x altura V = 50 cm x 20 cm x 15 cm V = 15000 cm³ (centímetros cúbicos) Como foi informado que 1 cm³ corresponde a 1 ml, temos que 15000 cm³ é igual a 15000 ml ou 15 litros. |
Cubo
O cubo é um poliedro regular pois as suas faces são geometricamente iguais.
O cubo tem os seguintes elementos:
- 6 faces, que são quadrados geometricamente iguais;
- 12 arestas iguais, que são segmentos de recta;
- 8 vértices, que são pontos.

Diagonal do cubo
é dado pela fórmula D = a√3 onde a = o comprimento da aresta do cubo
Exemplo:
A área total de um cubo é 54 cm². Calcule a medida da diagonal desse cubo.
Resolução:
Ac = 6a² dc = a√3
54 = 6a² dc = 3√3cm²
54 /6 = a²
a = √9
a =3 cm
Área lateral do cubo
A área lateral do cubo é a soma das áreas das faces laterais, sendo dada por:
Al = 4a2 , onde: Al - área lateral
A área total do cubo é a soma da área lateral com a área das duas bases, ou seja:
At = Al + 2Ab = 4a2 + 2a2 = 6a2, onde: At - área total
Al = 4a2 - área lateral
Ab = a2 - área da base
Volume do cubo
É dado pelo cubo (terceira potência) do comprimento da aresta. Assim, sendo a o comprimento da aresta do cubo, o seu volume é
V=a3
Exemplo:
Se a soma das medidas de todas as arestas de um cubo é 60 cm,então o volume desse cubo, em centímetros cúbicos, é:
Resolução:
12 arestas
60 cm / 12 = 5
V = 5³ = 125 cm³
Volume de um prisma
:
Resolução:
12 arestas
60 cm / 12 = 5
V = 5³ = 125 cm³
V = Ab . h onde: Ab é a área da base e h a altura do prisma
Exemplo:
Calcule o volume de um prisma cuja a altura mede 15cm e seus catetos, 9cm e 12cm.

Resolução:
Basta calcular a área do triângulo da base:
Ab = b * h /2
Ab = 9 * 12 /2
Ab = 54 cm²

Nenhum comentário:
Postar um comentário