Uma pirâmide é um poliedro, cuja base é um polígono qualquer e cujas faces laterais são triângulos com um vértice comum, que é o vértice da pirâmide.
classificação das pirâmides
Pirâmide regular
Pirâmide irregular
Pirâmide convexa
Pirâmide côncava
Pirâmide reta
Pirâmide obliqua
Classificação das pirâmides segundo sua basePirâmide triangular
Pirâmide quadrangular
Pirâmide pentagonal
Pirâmide hexagonal
4) Calcular a área lateral de uma pirâmide quadrangular regular que tem 12cm de altura e 40cm de perímetro da base.
5) Qual é a área total de uma pirâmide quadrangular regular, sabendo-se que sua altura mede 24cm e que o apótema da pirâmide mede 26cm?
6) A área lateral de uma pirâmide quadrangular regular de altura 4m e de área da base 64m² vale:
7) Uma pirâmide quadrada tem todas as arestas medindo 2. A altura mede:
8) (UnB) Sejam Pi e P2 duas pirâmides de mesma altura. A base de Pi é um quadrado e a de P2 um triângulo de área igual a do quadrado. Então, a área lateral de Pi é:
a) sempre maior do que a de P2;
b) sempre menor do que a de P2;
c) sempre igual a de P2;
d) n.d.a.
9) (OSEC) Um prisma e uma pirâmide tem bases com a mesma área. Se o volume do prisma é o dobro do volume da pirâmide, a altura da pirâmide será:
a) O triplo da do prisma.
b) O dobro da do prisma.
c) O triplo da metade da do prisma.
d) O dobro da terça parte da do prisma.
e) n.d.a
10) (Unirio) As arestas laterais de uma pirâmide reta medem 15cm, e a sua base é um quadrado cujos lados medem 18cm. A altura dessa pirâmide, em cm, é igual a:
a) 2√7 b) 3√ 7 c) 4√7 d) 5√7
11) (FEI - MAUÁ) Secciona-se uma pirâmide regular de altura h por um plano paralelo à base, a uma distância x do vértice. Pede-se x de modo que a áreas laterais da pirâmide se altura x e do tronco de pirâmide de altura h - x sejam iguais.
12) (MAUÁ) Na pirâmide VABC os ângulos AVB, BVC e CVA são retos. Calcular a distância de V ao Plano ABC sabendo-se que VA = VB = VC = 1m.
13) (UFRS) A base de uma pirâmide tem área igual a 225cm². A 2/3 do vértice, corta-se a pirâmide por um plano paralelo à base. A área da secção é igual a:
a) 30 b) 50 c) 70 d) 90 e) 100
Gabarito:
4) 260cm² 5) 1440cm² 6) 64√2 m² 7) √2 8) D 9) C 10) B 11) h√2 /2 12)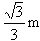 13) E
13) E
5) Qual é a área total de uma pirâmide quadrangular regular, sabendo-se que sua altura mede 24cm e que o apótema da pirâmide mede 26cm?
6) A área lateral de uma pirâmide quadrangular regular de altura 4m e de área da base 64m² vale:
7) Uma pirâmide quadrada tem todas as arestas medindo 2. A altura mede:
8) (UnB) Sejam Pi e P2 duas pirâmides de mesma altura. A base de Pi é um quadrado e a de P2 um triângulo de área igual a do quadrado. Então, a área lateral de Pi é:
a) sempre maior do que a de P2;
b) sempre menor do que a de P2;
c) sempre igual a de P2;
d) n.d.a.
9) (OSEC) Um prisma e uma pirâmide tem bases com a mesma área. Se o volume do prisma é o dobro do volume da pirâmide, a altura da pirâmide será:
a) O triplo da do prisma.
b) O dobro da do prisma.
c) O triplo da metade da do prisma.
d) O dobro da terça parte da do prisma.
e) n.d.a
10) (Unirio) As arestas laterais de uma pirâmide reta medem 15cm, e a sua base é um quadrado cujos lados medem 18cm. A altura dessa pirâmide, em cm, é igual a:
a) 2√7 b) 3√ 7 c) 4√7 d) 5√7
11) (FEI - MAUÁ) Secciona-se uma pirâmide regular de altura h por um plano paralelo à base, a uma distância x do vértice. Pede-se x de modo que a áreas laterais da pirâmide se altura x e do tronco de pirâmide de altura h - x sejam iguais.
12) (MAUÁ) Na pirâmide VABC os ângulos AVB, BVC e CVA são retos. Calcular a distância de V ao Plano ABC sabendo-se que VA = VB = VC = 1m.
13) (UFRS) A base de uma pirâmide tem área igual a 225cm². A 2/3 do vértice, corta-se a pirâmide por um plano paralelo à base. A área da secção é igual a:
a) 30 b) 50 c) 70 d) 90 e) 100
Gabarito:
4) 260cm² 5) 1440cm² 6) 64√2 m² 7) √2 8) D 9) C 10) B 11) h√2 /2 12)
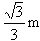 13) E
13) E











 onde: P
onde: P





 Para resolver é só ler bem a questão e saber interpretar, é bem simples de resolvé-la basta multiplicar a área (que o problema nos dá ) pelos lados do hexágono ( 6 ),ou seja , 12 X 6 = 72cm²
Para resolver é só ler bem a questão e saber interpretar, é bem simples de resolvé-la basta multiplicar a área (que o problema nos dá ) pelos lados do hexágono ( 6 ),ou seja , 12 X 6 = 72cm²
Nenhum comentário:
Postar um comentário