As principais operações são: adição, subtração, divisão e multiplicação. Utilizando o processo da multiplicação podemos encontrar outra operação: a potenciação, que para a realização de seus cálculos é necessário saber multiplicar.
Os números envolvidos em uma multiplicação são chamados de fatores e o resultado da multiplicação é o produto, quando os fatores são todos iguais existe uma forma diferente de fazer a representação dessa multiplicação que é a potenciação.
2 . 2 . 2 . 2 = 16 → multiplicação de fatores iguais.
Podemos representar a mesma multiplicação da seguinte forma:
2 . 2 . 2 . 2 = 24 = 16
↓
Fatores iguais.
Essa representação é conhecida como potenciação, portanto, sempre que tivermos fatores iguais, podemos montar uma potência.
Representamos uma potência da seguinte forma:
.jpg)
A base sempre será o valor do fator.
O expoente é a quantidade de vezes que o fator repete.
A potência é o resultado do produto.
Expoente negativo
Qualquer número diferente de zero elevado a um expoente negativo é igual ao inverso deste número elevado ao oposto do expoente:
.jpg)
Propriedades das potências
Multiplicação de potências de mesma base: “conservar a base e somar os expoentes”.
Exs: 22 . 23 = 22 + 3 = 25 = 32
Divisão de potências de mesma base: “conservar a base e subtrair os expoentes”.
Exs: 128 : 126 = 128 – 6 = 122 = 144
(-5)6 : (-5)2 = (-5)6 – 2 = (-5)4 = 625
Potência de potência
(3²)³ = (3 . 3)³ = 93 = 9 . 9 . 9 = 729
Utilizando a propriedade de potência, a resolução ficará mais simplificada: basta multiplicarmos os dois expoentes, veja:
(32)3 = 32 . 3 = 36 = 729
(-91)2 = (-9)1 . 2 = (-9)2 = 81
Multiplicação de potências de mesmo expoente: “conservar os expoentes e multiplicar as bases”.
Exs: (3 x 4)³ = 3³ x 4³ = 27 x 64 = 1728
(2 x 6)² = 2² x 6² = 144
Divisão de potências de mesmo expoente: “conservar os expoentes e dividir as bases”.
Exs: (3 x 4)³ = 3³ x 4³ = 27 x 64 = 1728
(2 x 6)² = 2² x 6² = 144
Divisão de potências de mesmo expoente: “conservar os expoentes e dividir as bases”.
Exs: 28³ : 7³ = 4³
64² : 8² = 8²
Número inteiro no expoente
.jpg)
.jpg)
Potência fracionária
Definição
Para um número real a e um inteiro positivo n (n ³ 2), definimos
desde que exista 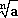 .
.
Façamos nosso estudo partindo de um número qualquer:
.png)
.png)
.png)
O numerador da potência corresponde ao expoente do número que está na base.
O denominador da potência corresponde ao grau da raiz. No nosso caso é uma raiz de grau 3 (raiz cúbica).
Fazer essa transformação de um número em uma raiz para um número com potência fracionária nos auxilia quando queremos multiplicar números de mesma base, porém em raízes de graus diferentes.
Vejamos o seguinte exemplo:
.png)
.png)
.png)
.png)
Podemos simplificar números elevados ao quadrado que estão dentro de uma raiz quadrada, pois o numerador e denominador são iguais. Vejamos alguns exemplos:
.png)
Potência de expoente 1.
Sempre que o expoente for igual a 1 o resultado será igual à base.
51 = 5
251 = 25
Potência de expoente zero.
Sempre que o expoente for igual a zero o seu resultado será igual a 1.
20 = 1
50 = 1
(-10)0 = 1
650 = 1
Deduzimos que toda potência de expoente zero é igual a 1, porque ao efetuarmos a divisão de potências de bases iguais e expoentes iguais, chegamos a valores diferentes veja:
43 : 43 = 43 – 3 = 40
43 : 43 = 1
Utilizamos dois métodos diferentes para a resolução da mesma divisão e encontramos dois resultados diferentes, portanto, concluímos que:
40 = 1
Assim, é possível concluir que toda potência de expoente zero será igual a 1.
Potência de base 10
Sempre que uma potência tiver base igual a 10 seu resultado será igual a 1, seguido de tantos zeros quantos forem as unidades do expoentes.
101 = 10
102 = 100
103 = 1000
104 = 10000
.png)
Sempre que o expoente for igual a 1 o resultado será igual à base.
51 = 5
251 = 25
Potência de expoente zero.
Sempre que o expoente for igual a zero o seu resultado será igual a 1.
20 = 1
50 = 1
(-10)0 = 1
650 = 1
43 : 43 = 43 – 3 = 40
43 : 43 = 1
Utilizamos dois métodos diferentes para a resolução da mesma divisão e encontramos dois resultados diferentes, portanto, concluímos que:
40 = 1
Assim, é possível concluir que toda potência de expoente zero será igual a 1.
Potência de base 10
Sempre que uma potência tiver base igual a 10 seu resultado será igual a 1, seguido de tantos zeros quantos forem as unidades do expoentes.
101 = 10
102 = 100
103 = 1000
104 = 10000
Potenciação de números racionais
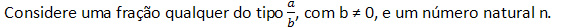
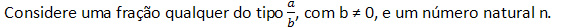
Temos que:
.jpg)
Sabemos que a multiplicação de frações é feita multiplicando numerador com numerador e denominador com denominador. Assim, segue que:
.jpg)
Observe que no numerador da fração resultante apareceram n fatores a e no denominador, n fatores b. Dessa forma, podemos reescrever a expressão anterior da seguinte maneira:
.jpg)
Note que a potenciação de frações é feita elevando o numerador e o denominador ao expoente n.
Seguem alguns exemplos para melhor compreensão.
Exemplo 1.Calcule o valor de cada uma das seguintes potências.
Seguem alguns exemplos para melhor compreensão.
Exemplo 1.
.jpg)
.jpg)
Exemplo 2. Determine o valor de cada potência abaixo:
.jpg)
Potenciação de monômio
Potência de um produto (a . b)m = am . bm
Potência de potência (am)n = am . n
Iremos aplicar essas duas propriedades no cálculo de potência de monômios. Por exemplo:
Dessa forma, podemos dizer que sempre que o expoente for negativo o resultado da potência será uma fração algébrica.
Potenciação de números negativos
(-4)³ = (-4) . (-4) = 16 . (-4) = -64
(-4)² = (-4) . (-4) = 16
(-4)² = (-4) . (-4) = 16
Com base nisso, podemos dizer que quando um número negativo é elevado a um número par, o resultado será positivo. Se for ímpar será negativo.
Nenhum comentário:
Postar um comentário