Artigo sobre radiciação e as propriedades dos radicais.
Pela definição de radiciação, temos que:
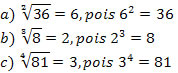
Não Existe a Raiz de um Radicando Negativo e Índice Par
Por quê?
Vamos tomar como exemplo a raiz quadrada de menos 16 expressa por 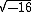 . Segundo a definição temos:
. Segundo a definição temos:
Qual é o valor numérico que b deve assumir para que multiplicado por ele mesmo seja igual a -16?
Como sabemos na multiplicação de números reais ao multiplicarmos dois números, diferentes de zero, com o mesmo sinal, o resultado sempre será positivo, então não existe um número no conjunto dos números reais que multiplicado por ele mesmo dará um valor negativo, pois o sinal é o mesmo em ambos os fatores da multiplicação.
A Raiz de um Radicando Negativo e Índice Ímpar é Negativa
Em uma multiplicação se todos os sinais forem positivos, obviamente o produto final também será positivo, já se tivermos fatores negativos, se estes forem em quantidade par o resultado será positivo, se forem em quantidade ímpar o resultado será negativo. É evidente que nenhum dos fatores pode ser igual a zero. Então a raiz enésima de a, um número real negativo será negativa se o índice for ímpar. Se for par como vimos acima, não existirá.
Vamos analisar a raiz quinta de menos 32 que se expressa como 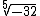 :
:
Como o expoente de b é ímpar, ou seja, o número de fatores que representa a potência é impar, para que o resultado seja -32, é preciso que b seja negativo. Então a raiz de um número negativo e índice ímpar sempre será um número negativo.
Neste exemplo -2 é o número negativo que elevado a 5 resulta em -32, logo:
Note que na potência colocamos o -2 entre parênteses, pois se não o fizéssemos, apenas o 2 estaria elevado à quinta potência. Como o expoente é ímpar, não faria diferença no resultado se não os tivéssemos utilizado, mas isto seria imprescindível se o expoente fosse um número par, para que não houvesse erro de sinal no resultado da potenciação.
A Raiz de um Radicando Positivo também é Positiva
Não importa se o índice é par ou impar, em não sendo nulo, a raiz de um radicando positivo também será positiva.
Vamos analisar a 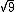 , que se lê raiz quadrada de nove:
, que se lê raiz quadrada de nove:
Logo 3 é o número que elevado ao quadrado dá 9.
Mas você pode também se perguntar:
E se for -3? Se elevarmos -3 ao quadrado também iremos obter nove!
Correto, mas lembra-se da definição da raiz para um radicando positivo?
Tanto o radicando quanto a raiz devem ser positivos, é por isto que não podemos considerar o -3.
Propriedades da radiciação
Vamos agora ver alguma propriedades fundamentais de radiciação:
an/n
e a fração n/n vale 1, então:
an/n = a1= a
Estas são as principais propriedades de Radiciação. Agora vamos ver as propriedades operatórias, ou seja, como fazer operações com raizes (multiplicação, divisão...).
PROPRIEDADES OPERATÓRIAS
Agora vamos dar uma visão mais genérica, visto que as propriedades irão se repetir pois são idênticas às de potênciação:
Novamente se transformarmos a raiz em potência, teremos:

Agora o que devemos fazer é voltar de potência para raiz:
É interessante observar que todas as propriedades de potências para expoentes inteiros positivos são válidas, também, para as potências de expoentes fracionários.
exercícios de fixação
1) Simplifique a expressão
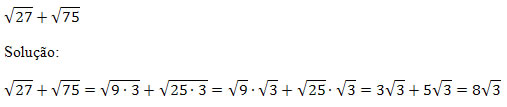
2) Racionalize as seguintes frações:
Racionalizar a fração é fazer com que no denominador não exista uma raiz enésima de um número.
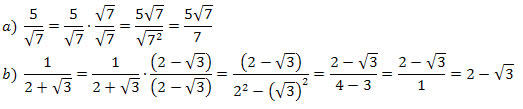
Racionalizar a fração é fazer com que no denominador não exista uma raiz enésima de um número.
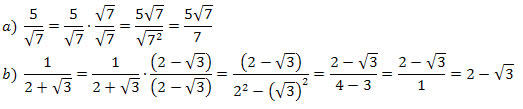
3) Verifique as propriedades da radiciação.
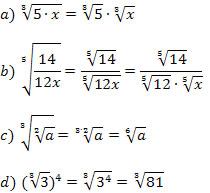
4)Obtenha a forma mais reduzida possível da expressão:
Solução: Podemos reescrever cada uma das raízes utilizando as propriedades da radiciação.

Estou feliz por ter encontrado um blog tão bom quanto este. Muito obrigado!
ResponderExcluir