Sabemos que a área de uma circunferência é diretamente proporcional ao tamanho do seu raio e é obtida fazendo π∙r², onde π equivale, aproximadamente, 3,14. O setor circular é uma parte da circunferência limitada por dois raios e um arco central. A determinação da área do setor circular depende da medida desse ângulo central e do comprimento do raio da circunferência.
.jpg)
Uma volta completa no círculo corresponde a 360º, valor que podemos associar à expressão do cálculo da área do círculo, π * r². Partindo dessa associação podemos determinar a área de qualquer arco com a medida do raio e do ângulo central, através de uma simples regra de três. Observe:
360º ------------- π * r²
θº ------------------ x
Onde:
π = 3,14
r = raio do círculo
θº = medida do ângulo central
x = área do arco
Exemplo: Determine a área do setor circular abaixo. (Use π = 3,14)
Solução: Como conhecemos o raio e a medida do ângulo central, basta substituir esses valores na fórmula da área do setor circular.
Exercícios área do setor circular
1) Numa circunferência de área igual a 121π cm², calcule a área do setor circular delimitado por um ângulo central de 120º.
Solução:
Para solução desse problema devemos verificar que no numerador da fórmula da área do setor circular, a medida do ângulo central α está multiplicando a área da circunferência, dessa forma teremos:
2) Determine a área de um segmento circular com ângulo central de 32º e raio medindo 2 m.
360º ------------- π * r²
32º ------------------ x
360x = 32 * π * r²
x = 32 * π * r² / 360
x = 32 * 3,14 * 2² / 360
x = 32 * 3,14 * 4 / 360
x = 401,92 / 360
x = 1,12
A área do segmento circular possui aproximadamente 1,12 m².
3) Determine a área do setor circular com ângulo central de 30º num círculo de 20 cm de raio.
solução:
A área do setor circular de 30º corresponde a um setor de π/6 rad, observe os cálculos:
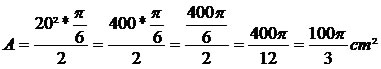
4)
muito besta
ResponderExcluirbom para provas de ultimo ano no fundamental
ExcluirEu diria isso de uma forma mais atenua,mas concordo.
ExcluirO que pode ser óbvio para alguns pode não ser para outros! Parabéns pelas indicações, mesmo que tenham sido, em sua maioria, cópia do site Brasil Escola. É sempre bom fazer a referência Cleiton Silva!
ResponderExcluirnão entendi nada
ResponderExcluirdou meu cu
ResponderExcluirMuito bom , principalmente para quem está iniciando o aprendizado.
ResponderExcluir