ângulos complementares e suplementares questões resolvidas

COMPLEMENTARES: são ângulos na qual a soma de suas medidas é igual a 90º e neste caso, um ângulo é o complemento do outro.

Ex.: 30^o e 50^o (30+50=90) ou
37^o e 53^o (37+53=90) ou
20^o e 70^o (20+70=90) ...

SUPLEMENTARES: são ângulos na qual a soma de  suas medidas é igual a 180º e neste caso, um ângulo é o suplemento do outro.

Ex.: 50^o e 130^o (50+130=180) ou
71^o e 109^o (71+109=180) ou
80^o e 100^o (80+100=180) ...

REPLEMENTARES: são ângulos na qual a soma de suas medidas é igual a 360º e neste caso, um ângulo é o replemento do outro.

Ex.: 30^o e 330^o (30+330=360) ou
300^o e 60^o (300+60=360) ou
111^o e 249^o (111+249=360) ...

Complemento de "X" = 90 - X
Suplemento do Complemento de "X" = 180 - ( 90 - X ) = 90 + X
Suplemento de "X" = 180 - X
Replemento do Suplemento de "X" = 360 - ( 180 - X ) = 180 + X

execícios resolvidos ângulo suplementares, complementares e replementares

O quíntuplo do suplemento do complemento de um ângulo é igual ao triplo do replemento do seu suplemento. O ângulo é:

:

Solução:

2) O suplemento do triplo do complemento da metade de um ângulo é igual ao triplo do complemento desse ângulo. Determine o ângulo.

Solução:

[ 180° - 3*( 90° - (x/2) ] = 3*( 90° - x )

[ 180° - 270° + (3/2)x ] = 270° - 3x

(3/2)x + 3x = 270° + 90°

3x + 6x = 720°

9x = 720

x = 80°

DATAHOSTING.COM.BR|DE http://www.datahosting.com.br/afiliados/ok.php?id=8893

HOSPEDAGEM DE SITES R$14,90 com 10GB de Espaço e 150GB de Tráfego, Construtor de Sites e...

Hospedagem de sites com planos gigantes a partir de R$14,90, 10GB de espaço, 150Gb de tráfego de

DATAHOSTING.COM.BR|DE WWW.DATAHOSTING.COM.BR

3) Calcule o valor de x na figura.

Solução:

Os ângulos da figura são complementares, isto é, a soma entre eles é igual a 90º.
x + 40 + 3x + x – 10 = 90
5x + 30 = 90
5x = 90 – 30
5x = 60
x = 12

5) (FAM-SP) Os ângulos são suplementares, isto é, a soma entre eles é igual a 180º.

Solução:

2x + 30 + x = 180
3x = 180 – 30
3x = 150
x = 150/3
x = 50º

Resposta correta alternativa d.

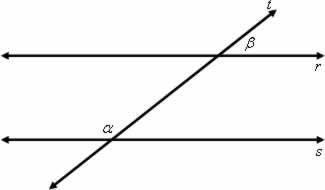
6) (Uniube–MG) Na figura abaixo, as retas r e s são paralelas, cortadas por uma transversal t. Se a medida do ângulo α é o triplo da media do ângulo β, então a diferença α – β vale:

a) 90º

b) 85º

c) 80º

d) 75º

e) 60º

Solução:

β: x
α: 3x

α + β = 180º
x + 3x = 180
4x = 180
x = 180 / 4
x = 45º

β: 45º
α: 135º

α – β  → 135º – 45º → 90º

Resposta correta alternativa  A.

7) (FUVEST-SP) Se α e β são dois ângulos complementares, então o determinante da matriz:

é igual a:

(A) -6

(B) -2

(C) 0

(D) 2

(E) 6

Solução:

- Ângulos complementares são ângulos que somados tem como resultado 90°

Como o determinante dessa matriz será:

Sen(α)Cos(β)*2*0 + 1*1*2 + (-1)*Sen(β)Cos(α)*4 - (-1)*2*2 - 1*4*Sen(α)Cos(β) - 0*1*Sen(β)Cos(α)
= 0 + 2 - 4Sen(β)Cos(α) + 4 - 4Sen(α)Cos(β) - 0 = 6 - 4Sen(β)Cos(α) - 4Sen(α)Cos(β)

Mas, das propriedades trigonométricas sabe-se que:
Sen(a + b) = Sen(a)Cos(b) + Sen(b)Cos(a)

Logo:
Det = 6 - 4Sen(β)Cos(α) - 4Sen(α)Cos(β) = 6 - 4*[Sen(β)Cos(α) + Sen(α)Cos(β)]
Det = 6 - 4*[Sen(α + β)]
Det = 6 - 4*[Sen(90°)]
Det = 6 - 4*[1] = 6 - 4 = 2

alternativa D a resposta correta.

DATAHOSTING.COM.BR|DE http://www.datahosting.com.br/afiliados/ok.php?id=8893

HOSPEDAGEM DE SITES R$14,90 com 10GB de Espaço e 150GB de Tráfego, Construtor de Sites e...

Hospedagem de sites com planos gigantes a partir de R$14,90, 10GB de espaço, 150Gb de tráfego de

DATAHOSTING.COM.BR|DE WWW.DATAHOSTING.COM.BR