Elementos de um círculo ou circunferência
Dada uma região circular, podemos ter: raio, diâmetro, corda, centro, arcos. Veja a figura:
.jpg)
segmento de reta AB: corda (segmento que parte de um ponto ao outro da circunferência)
segmento de reta DF: diâmetro (corda que passa pelo centro do círculo)
segmento de reta OF e OD: raio (segmento de reta que liga o centro a um ponto da circunferência)
Ângulo Central Ângulo central relativo a um círculo é o ângulo que tem o vértice no centro do círculo. Observe na figura que AÔB é um ângulo central, sendo o arco AB correspondente ao ângulo, ou seja, α = AB.
.jpg)
Ângulo inscrito
Ângulo inscrito relativo a um círculo é um ângulo que tem o vértice no círculo e os lados são secantes a ele.
Um ângulo inscrito é metade do ângulo central correspondente; ou pode-se dizer: a medida de um ângulo inscrito é metade da medida do arco correspondente, ou seja:

Relação entre ângulo central e ângulo inscrito
Ao analisarmos uma circunferência e constatarmos que o ângulo central e o ângulo inscrito possuem o mesmo arco, podemos dizer que o valor do ângulo central é o dobro do valor do ângulo inscrito.
Exemplo:
1 – Qual o valor do ângulo central indicado por x na figura:
x = 2 *42º
x = 84º
.jpg)
ângulo circunscrito
É o ângulo, cujo vértice não pertence à circunferência e os lados são tangentes à ela.

ângulo de segmento
É todo ângulo cujo vértice pertence à circunferência, sendo um de seus lados secante e o outro tangente à circunferência. A medida de um ângulo de segmento é igual à metade do arco por ele determinado.

Ângulo com vértice exterior à circunferência – Ângulo excêntrico externo.
A medida de um ângulo de vértice interno é igual à semi-soma das medidas dos arcos determinados pelos seus lados.
A medida de um ângulo de vértice interno é igual à semi-soma das medidas dos arcos determinados pelos seus lados.
Exemplo: Determine o valor de α na figura abaixo.
A medida de um ângulo de vértice externo é igual à semi-diferença dos arcos de terminados pelos seus lados.
Exemplo: Determine o valor de α na figura abaixo.
Solução:
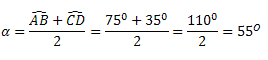
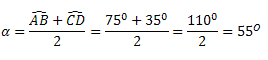


Boa tarde! Você inverteu os conceitos de ângulo de vértice interno e externo. Obg!
ResponderExcluirDesculpe
Excluirme ajodou muito em um trabalho escolar! obg.
ResponderExcluira j o d o u
Excluireu espero que me ajude na minha prova hoje de geometria onde eu só tiro 5,5 ai eu quero tirar mas do que isso né mas eu gostei ta faltando mas coisa mas para me já esta mas do que explicado to aprendendo mesmo que geometria seja o oh
ResponderExcluirportuguês mandou abraços
ExcluirAs contas estão certas?
ResponderExcluirsou professor de matemática tenho mestrado em estatistica e trabalho como professor na UFABC e vejo que seus cálculos e esquemas nao estao corretos
ResponderExcluirAaaai.. Legal.. Mas ta muito conceito.. Contextualize mais.. Traz umas atividades mais contextualizadas, indiretas.. Essas atividades sao aplicações de formulas diretas.. Fica a dica��
ResponderExcluirinutil , toma vergonha na cara
ResponderExcluirSó fica mandando merda na internet pois pq tu n fez o site se achou inútil
Excluirsocorro
ResponderExcluirMe ajudou muito no trabalho da escola
ResponderExcluir