Determinantes: propriedades e Teorema de LaPlace

As dificuldades que podem ocorrer no cálculo de determinantes dependem naturalmente da ordem e dos elementos da matriz considerada. As propriedades que estudaremos a seguir poderão ajudar na simplificação desse cálculo.

Primeira propriedade

Se os elementos de uma fila de uma matriz quadrada forem iguais a zero, seu determinante será nulo.

Exemplo:

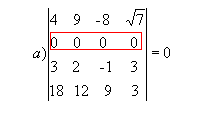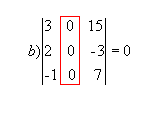Segunda propriedade

O determinante de uma matriz é igual ao determinante de sua transposta. 
det R=det R^t

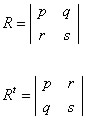
det R = ps -- qr 

det Rt = ps – rq 

Terceira propriedade

Se uma matriz quadrada tem duas filas paralelas iguais, seu determinante será nulo.

Exemplo:

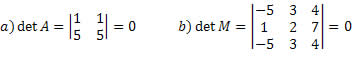
Quarta propriedade

Se duas filas paralelas de uma matriz são proporcionais, então seu determinante é nulo.



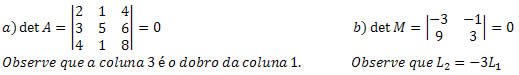
Quinta propriedade

Se todos os elementos de uma linha ou de uma coluna da matriz forem multiplicados por um número real p qualquer, então seu determinante também será multiplicado por p.

Os elementos da 1ª linha de P foram multiplicados por 2, então: det P’ = 2 * det P 

Sexta propriedade

Quando trocamos duas colunas ou duas linhas de posição de uma matriz, o valor do seu determinante será  oposto ao determinante da anterior. 

Exemplo:

Sétima propriedade

O determinante de uma matriz triangular é igual à multiplicação dos elementos da diagonal principal. 
Lembre-se que em uma matriz triangular, os elementos acima ou abaixo da diagonal principal são iguais a zero.

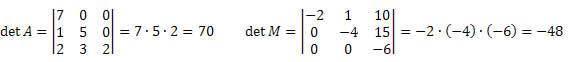
Oitava propriedade

Teorema de Jacobi: Um determinante não se altera quando somamos a uma fila outra fila paralela multiplicada por um número real qualquer.

Exemplo:

Se somarmos os elementos da coluna 1 com o dobro dos elementos da coluna 2, o determinante não irá se alterar.

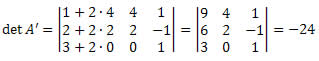
Nona propriedade 

Considerando duas matrizes quadradas de ordem iguais e AB matriz produto temos que: det (AB) = (det A) * (det B), conforme teorema de Binet. 

Décima propriedade

Caso uma matriz quadrada A seja multiplicada por um número real k, seu determinante passa a ser multiplicado por kⁿ. 
det (k*A) = kⁿ * det A 

Teorema de laPlace

 Consiste num método de cálculo do determinante de matrizes quadradas de ordem n ≥ 2 utilizando o cofator.

Lembre-se: o cofator do elemento aij de uma matriz quadrada é:

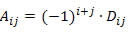
Para aplicar o teorema de la place devemos escolher qualquer fila (linha ou coluna) da matriz B e multiplicar cada elemento da fila pelo seu respectivo cofator. O resultado da matriz B será a soma dos produtos dos elementos da fila pelos seus respectivos cofatores.

Calcule o determinante da matriz a seguir utilizando o Teorema de Laplace.

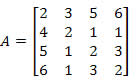
Solução: Devemos escolher uma linha ou uma coluna da matriz A.

Se escolhermos a coluna 2, teremos:

Pelo teorema de Laplace, sabemos que:
D = a₁₂∙A₁₂ + a₂₂∙A₂₂ + a₃₂∙A₃₂ + a₄₂∙A₄₂

Segue que:

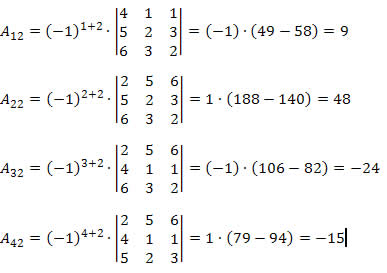
Assim, o determinante da matriz A será:

D = 3∙9 + 2∙48 + 1∙(-24) + 1∙(-15) = 27 + 96 - 24 - 15 = 84

Veja também:

Determinantes (regra de Saurus, cofator)

Exercícios Determinantes vestibular

Sistemas de equações lineares (Regra de Cramer, matriz de um sistema linear)

Exercícios Determinantes vestibular