1) (Fatec-SP - Adaptada) Suponhamos que a população de uma certa cidade seja estimada, para daqui a x anos, por  . Determine a população referente ao terceiro ano.
. Determine a população referente ao terceiro ano.
 . Determine a população referente ao terceiro ano.
. Determine a população referente ao terceiro ano. A população referente ao 3º ano é de 19.875 habitantes.
A população referente ao 3º ano é de 19.875 habitantes.
2) (PUCC-SP) Numa certa cidade, o número de habitantes, num raio de r jm a partir do seu centro é dado por P(r) = k * 23r, em que k é constante e r > 0. Se há 98 304 habitantes num raio de 5 km do centro, quantos habitantes há num raio de 3 km do centro?
P(r) = k * 23r
98 304 = k * 2 3*5
98 304 = k * 215
98 304 = k * 32 768
k =98 304 / 32 768
k = 3
Calculando o número de habitantes num raio de 3 km
P (r) = k * 23r
P (3) = 3 * 23*3
P (3) = 3 * 29
P (3) = 3 * 512
P(3) = 1536
O número de habitantes num raio de 3 km é igual a 1536.
3) Se  , então "x" vale:
, então "x" vale:
a)  b)
b)  c)
c) 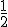 d)
d)  e)
e) 
Resolução:
Primeiro vamos transformar os decimais (números com vírgula) em frações:
Veja que podemos simplificar a fração da esquerda e transformar em potência o lado direito da igualdade:
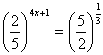
-As bases estão quase igualadas, só que uma é o inverso da outra. Vamos inverter uma delas e adicionar o expoente "-1".
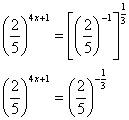
- Agora sim, com as bases igualadas podemos cortá-las:
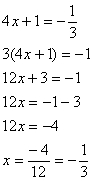 Resposta certa letra "A".
Resposta certa letra "A".4) A partir dos gráficos das funções f(x)=2x, g(x)=2x+2 e h(x)=2-x, descreva o que ocorre com g=g(x) e h=h(x) em relação a f=f(x).
Resolução:
O gráfico da função g(x)=2+2x é obtido de f(x)=2xtransladado verticalmente (no eixo y) por 2 unidades. O gráfico da função h(x)=(1/2)x é uma linha simétrica em relação ao eixo dos y (como se estivesse espelhada) que corresponde à função a f.
5) (EU-PI) Suponha que, em 2003, o PIB (Produto Interno Bruto) de um país seja de 500 bilhões de dólares. Se o PIB crescer 3% ao ano, de forma cumulativa, qual será o PIB do país em 2023, dado em bilhões de dólares? Use 1,0320 = 1,80.
Resolução:
P(x) = P0 * (1 + i)t
P(x) = 500 * (1 + 0,03)20
P(x) = 500 * 1,0320
P(x) = 500 * 1,80
P(x) = 900
O PIB do país no ano de 2023 será igual a R$ 900 bilhões.
6) Qual o domínio da função exponencial y = 2x ?
Sabemos que o domínio de uma função y = f(x) é o conjunto de valores que podem ser atribuídos a x. Observe que x sendo um expoente, ele poderá assumir qualquer valor e, portanto, o domínio da função dada é o conjunto dos números reais, ou seja:
D = R.
7) (IPA/IMEC) Se 2x+2-x=10 então 4x+4-x vale
Aplicando as propriedades de potenciação, o que o exercício dá e pede é:

- Este problema é o tipo de exercício que se você nunca viu como se faz, nunca iria conseguir fazer. Para resolvê-lo devemos pegar a equação dada e elevar ao quadrado ambos os lados. Veja só:
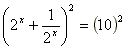
- Agora devemos efetuar ambos os lados. Não esqueça da regra para o produto notável da esquerda:
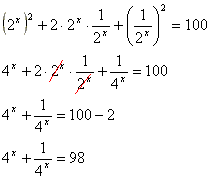 Resposta certa letra "D".
Resposta certa letra "D".
8) (ENEM-2009) Considere que uma pessoa decida investir uma determinada quantia e que lhe sejam apresentadas três possibilidades de investimento, com rentabilidades líquidas garantidas pelo período de um ano, conforme descritas:

a) M(t) = 24−t/75
b) M(t) = 24−t/50
c) M(t) = 25−t/50
d) M(t) = 25−t/150
Resolução
M(t) = 24 - t/75
v(10) = v0 * 2 –0,2*10
12 000 = v0 * 2 –2
12 000 = v0 * 1/4
12 000 : 1/ 4 = v0
v0 = 12 000 * 4
v0 = 48 000
11) (UFCE ) Se f ( x ) = 16^(1+1/x), então f ( -1 ) + f ( -2 ) + f ( -4 ) é igual a :
a. 11
b. 13
c. 15
d. 17
e. nda
Resolução:
Outra questão simples .. basta calcular a função substituindo o x ....
f(-1) = 16^(1+1/-1)
f(-1) = 16^(1 - 1)
f(-1) = 16^0
f(-1) = 1 ...
f(-2) = 16^(1- 1/2)
f(-2) = 16^1/2 ....SEMPRE se lembre que denominador de expoente é raiz ... logo denominador 2 é raiz quadrada:
f(-2) = V16
f(-2) = 4 ...
f(-4) = 16^(1- 1/4)
f(-4) = 16^(3/4)
f(-4) = ∜16³
f(-4) = 2³
f(-4) = 8 .... assim a soma vale
1 + 4 + 8 = 13 ...
Alternativa b.
12) Identifique o intervalo cujos valores de k tornam a função exponencial ,
,

a) 4 b) 2 c) 0 d) -2 e) -4
Vamos desenhar o gráfico desta função:
GANHE DINHEIRO ON LINE NO POSTMONEYS PARA SABER MAIS CLIQUE NO LINK ABAIXO:
www.superposts.com.br/pub.asp?cp=1598059
D = R.
7) (IPA/IMEC) Se 2x+2-x=10 então 4x+4-x vale
a) 40 b) 50 c) 75 d) 98 e) 100
Resolução:
- Este problema é o tipo de exercício que se você nunca viu como se faz, nunca iria conseguir fazer. Para resolvê-lo devemos pegar a equação dada e elevar ao quadrado ambos os lados. Veja só:
- Agora devemos efetuar ambos os lados. Não esqueça da regra para o produto notável da esquerda:
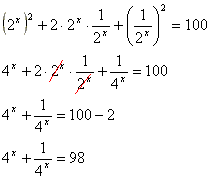 Resposta certa letra "D".
Resposta certa letra "D".8) (ENEM-2009) Considere que uma pessoa decida investir uma determinada quantia e que lhe sejam apresentadas três possibilidades de investimento, com rentabilidades líquidas garantidas pelo período de um ano, conforme descritas:
Investimento A: 3% ao mês
Investimento B: 36% ao ano
Investimento C: 18% ao semestre
As rentabilidades, para esses investimentos, incidem sobre o valor do período anterior. O quadro fornece algumas aproximações para a análise das rentabilidades:

Para escolher o investimento com a maior rentabilidade anual, essa pessoa deverá
A) escolher qualquer um dos investimentos A, B ou C, pois as suas rentabilidades anuais são iguais a 36%.
B) escolher os investimentos A ou C, pois suas rentabilidades anuais são iguais a 39%.
C) escolher o investimento A, pois a sua rentabilidade anual é maior que as rentabilidades anuais dos investimentos B e C.
D) escolher o investimento B, pois sua rentabilidade de 36% é maior que as rentabilidades de 3% do investimento A e de 18% do investimento C.
E) escolher o investimento C, pois sua rentabilidade de 39% ao ano é maior que a rentabilidade de 36% ao ano dos investimentos A e B.
RESOLUÇÃO:
Galera, vamos calcular quanto vai render cada um dos investimentos.
→ Investimento A: Rende 3% ao mês.
100% + 3% =103% = 1,03
Durante 12 meses teremos 1,0312 = 1,426 do valor inicial. (consulte a tabela)
→ Investimento B: Rende 36% ao ano.
100% + 36% =136% = 1,36
Durante 1 ano teremos 1,36 do valor inicial.
→ Investimento C: Rende 18% ao semestre.
100% + 18% =118% = 1,18
Durante 2 semestres teremos 1,182 = 1,3924 do valor inicial
Portanto, o investimento de maior rentabilidade no ano é o Investimento A.
Gabarito letra C.
9) (Unicamp - 2011) Em uma xícara que já contém certa quantidade de açúcar, despeja-se café. A curva abaixo representa a função exponencial M(t), que fornece a quantidade de açúcar não dissolvido (em gramas), t minutos após o café ser despejado. Pelo gráfico, podemos concluir que
a) M(t) = 24−t/75
b) M(t) = 24−t/50
c) M(t) = 25−t/50
d) M(t) = 25−t/150
Resolução
- Para o ponto (0,16), temos:
- Para o ponto (150,4), temos:
M(t) = 24 - t/75
10) (Unit-SE) Uma determinada máquina industrial se deprecia de tal forma que seu valor, t anos após a sua compra, é dado por v(t) = v0 * 2 –0,2t, em que v0 é uma constante real. Se, após 10 anos, a máquina estiver valendo R$ 12 000,00, determine o valor que ela foi comprada.
Resolução:
Resolução:
Temos que v(10) = 12 000, então:
v(10) = v0 * 2 –0,2*10
12 000 = v0 * 2 –2
12 000 = v0 * 1/4
12 000 : 1/ 4 = v0
v0 = 12 000 * 4
v0 = 48 000
A máquina foi comprada pelo valor de R$ 48 000,00.
a. 11
b. 13
c. 15
d. 17
e. nda
Resolução:
Outra questão simples .. basta calcular a função substituindo o x ....
f(-1) = 16^(1+1/-1)
f(-1) = 16^(1 - 1)
f(-1) = 16^0
f(-1) = 1 ...
f(-2) = 16^(1- 1/2)
f(-2) = 16^1/2 ....SEMPRE se lembre que denominador de expoente é raiz ... logo denominador 2 é raiz quadrada:
f(-2) = V16
f(-2) = 4 ...
f(-4) = 16^(1- 1/4)
f(-4) = 16^(3/4)
f(-4) = ∜16³
f(-4) = 2³
f(-4) = 8 .... assim a soma vale
1 + 4 + 8 = 13 ...
Alternativa b.
12) Identifique o intervalo cujos valores de k tornam a função exponencial
f(x) = (5k – 1)x decrescente.
A) 1/5 < k < 2/5
B) 0 < k < 1/5
C) k < 2/5
D) k > 1/5
E) k < 1
Resolução:
Para identificar o intervalo, devemos lembrar da seguinte propriedade da função exponencial:
Na função exponencial, cuja lei dada por f(x) = ax se 0 < a < 1, então a função é decrescente.
Veja, na lei de formação da função, a é a base da potência e deve estar entre 0 e 1 exclusivos.
Portanto, para que a função f do enunciado, dada pela lei f(x) = (5k – 1)x seja decrescente, devemos ter
0 < 5k – 1 < 1.
Resolvendo:
0 < 5k – 1, então 1 < 5k, logo 1/5 < k.
5k – 1 < 1, então 5k < 2, logo k < 2/5.
Logo, para que a função seja decrescente devemos ter 1/5 < k < 2/5.
13) Determinar o conjunto solução da equação 3x-34-x=24.
Resolução:
Como 34-x=34.3-x=81/3x, obtemos 3x-81/3x=24
Com a mudança de variável 3x=y, obteremos y-81/y=24
Multiplicando ambos os membros desta equação por y, obtemos a equação do segundo grau: y2-24y-81=0
Usando a fórmula quadrática, obtemos duas raízes reais

dadas por y1=27 e y2=-3 e como esta equação possui duas raizes reais, temos dois casos a considerar:
Caso 1: Se y1=27 então 3x=27=33, portanto x=3.
Caso 2: Se y2=-3 então 3x=-3. Como f(x)=3x é sempre positiva, esta função não pode assumir um valor negativo. Assim S={x em R: x=3}
14) (FUVEST-2013) Seja f(x) = a + 2^bx + c, em que a, b e c são números reais. A imagem de f é a semirreta ]-1, [ e o gráfico de f intercepta os eixos coordenados nos pontos (1,0) e (0,-3/4). Então o produto abc vale:
a) 4 b) 2 c) 0 d) -2 e) -4
Vamos desenhar o gráfico desta função:
Vamos analisar uma parte da função f(x). Iremos chamar a parte 2bx+ c de g(x).
A função g(x) = 2bx+ c tem a seguinte imagem:
Im g(x) = ]0, + ∞[ , para todo x pertencente aos reais.
Mas a função f(x) tem uma constante “a” somada com a função g(x). E a questão nos informa que o intervalo neste caso é:
Im f(x) = ]-1, + ∞[
A soma de uma constante numa função exponencial faz com que ela se desloque sobre o eixo y (conjunto-imagem) e mude o valor do intervalo aberto à esquerda que será exatamente o da constante.
Na função f(x) temos a constante “a” e o valor do intervalo aberto à esquerda é -1. Portanto, a = -1.
Já temos o valor de “a”. Precisamos agora do valor de b e c.
A questão nos informa também que a função f(x) passa pelos pontos (1,0) e (0,-3/4).
Vamos ver o ponto (1,0):
Neste caso, temos x = 1 e y = f(1) = 0.
Logo,
f(x) = a+ 2bx+ c
f(1) = -1+ 2bx+ c
0 = -1 + 2b1+ c
-1 + 2b1+ c = 0
2b+ c = 20
b + c = 0
b = -c
Agora veremos o ponto (0,-3/4):
Neste caso, temos x = 0 e y = f(0) = -3/4.
Logo,
f(x) = a+ 2bx+ c
f(0) = -1+ 2bx+ c
-3/4 = -1 + 2b0+ c
1 – 3/4 = 2c
1/4= 2c
2c = 1/4
2c = 2-2
c = -2
Mas b = -c. Logo, b = 2
Portanto, a = -1, b = 2 e c =-2
Logo, a.b.c = (-1).2.(-2) = 4
a.b.c = 4
ALTERNATIVA A
GANHE DINHEIRO ON LINE NO POSTMONEYS PARA SABER MAIS CLIQUE NO LINK ABAIXO:
www.superposts.com.br/pub.asp?cp=1598059




uma merda, como qualquer assunto de matemática
ResponderExcluirrealmente.
ExcluirPodiam ir jogar video game, aqui é lugar de coisa séria.
Excluir!!!... também acho , é lugar para quem quer alguma coisa... para qm quer sem alguem na vida
Excluir.....
Eu sou uma pessoa, então sou um alguém, que está vivo, então sou um alguém na vida, mas não gosto de matemática!!!!!!! E sua ideia de ser alguém na vida, é uma ideia capitalista, um alguém na vida pra você, é uma pessoa que estuda só para ganhar dinheiro e mais dinheiro!!!!! Babaca!
ExcluirE não vou voltar mais nessa porra, porque tenho mais coisa interessante para fazer do que ficar respondendo suas críticas....assinado: uma pessoa negra gorda e bissexual ( pessoas alvos de críticas da sociedade). rs. Achei ofensivo da parte de vocês, vou lavar louça..
Excluirnossa cara como vocês são legais '-'
ExcluirEsse vitimismo me comoveu, vou chorar aqui. Falou.
Excluirparabén, você continuará a ser alvo de críticas agindo dessa maneira, e ainda por cima usa isso a seu favor se fazendo de vítima, coisa de ignorante, é por isso que o Brasil esta assim
ExcluirO seu problema não é ser gordo, negro e bissexual; o seu problema é ser um babaca escroto que se esconde atrás de três coisas, sendo que duas você buscou ser, que são: ser gordo e bissexual. Ninguém te forçou a ser gordo e nem a ser bissexual, então para de frescura e vai estudar algo mais nobre do que esse lixo comunista.
ExcluirEsse vitimismo não te levará a ser um pobre imbecil. Você fala mal do capitalismo, mas garanto que é louco pra ser um rico boçal, que humilhará os outros. Nunca conheci um comunista não capitalista de verdade.
O problema de vocês comunistas fracassados é que nós capitalistas corremos atrás de ser alguém e conseguimos. Isso se chama meritocracia, cumpanheiro.
Have a nice day!!!
quero mais! vou resolver qualquer questão sem ter dificuldade.
ResponderExcluirTambém,esses exercícios só serviram para me aquecer.Mas,mesmo assim,o site é bom.Anônimo acima,este site tem bons exemplos também. http://www.somatematica.com.br/superior/logexp/logexp4.php
Excluirisso dói meu cérebro, velho.
ResponderExcluirOdeioooooooo matematica!
ResponderExcluirsomos Dois,,,,,,= matematica é coisa do bixo! kkk
Excluirdois burro!
Excluirentao vai pentear macaco
ResponderExcluirPor favor, exercicios fáceis, não entendi!
ResponderExcluirxx
A matemática é simples porém muito eficiente. se tiveres calma e se dedicar será um bom matemático
ResponderExcluirE vc é um idiota!""
ExcluirPessoas que odeiam matemática é por que não estudam por isso, mané
ExcluirUma correção, no primeiro exercício aparece 159.000.000/8 .. Porém é 159.000, pois 159 é multiplicado por 1000. Até mais.
ResponderExcluirmatematica não é dificil ,tendo força de vontade pra estudar exercitar ela n se torna dificil ,pois ela é mais pratica do que as outras que voce tem que decorar paragrafos pra prova,matematica esta em qualquer lugar até no ser humano ,basta olhar para o lado bom dela garanto que não vão se arrepender,pois as profissoes mais bem pagas envolvem ela :matemática .
ResponderExcluirmatemática ser difícil ou não é algo relativo, ou seja o que é fácil pra você não tem o mesmo nível de facilidade para o outro que não se identifica com a matéria, não generalize a sua capacidade de entender a matéria com a do outro. Pois eu como uma pessoa que não tem um pingo de interesse por ser bom em exatas acho isso totalmente inútil pra mim, pois é algo que não me interessa nem um pouco.Fica a dica.
ExcluirPerfeito ;D
ResponderExcluirMATEMATICA MZERAVI '-'
ResponderExcluirGostei da resposta às críticas no 5 comentário ��.... Não gostar de matemática, não significa que vc não será merda!!!
ResponderExcluirA pior matéria
ResponderExcluirque existe
amo matemática, pois ela é minha vida através do estudo da matematica que consegui as coisas na minha vida!!!! ass. professora de matematica
Excluirisso torra o meu cerebro meuuuuuuuuuuu
ResponderExcluirsem graça!
ResponderExcluirñ entendi nada desse site.
ResponderExcluirOdeio isso, Meu Deus estou enllouquecendo........
ResponderExcluirIsto é para poucos.E garanto, este pouco são os mais dedicados.
ExcluirEu amo esse blog <3
ResponderExcluirAdorei! Me ajudou bastante
ResponderExcluirlorena marina eu ti keru gostosaa
ResponderExcluirMuito bom o blog e contém ótimas explicações.
ResponderExcluirMeu Deus me ajude nessa prova ;-; Matemática não é pra mim sou de humanas, quando me formar espero usar isso o minimo possivel, tenho a certeza que na padaria\supermercado\vida tudo que tenho que fazer é entregar o dinheiro do pão e não calcular a massa do pão x o horario que comi o pão vez o preço do pão e a distancia do sol para terra
ResponderExcluirsou de humanas
ResponderExcluirGostei de tudo por aqui...Inclusive os papos filosóficos...kkk
ResponderExcluirGostei de tudo por aqui...Inclusive os papos filosóficos...kkk
ResponderExcluirAdorei muito....... kkkkkk
ResponderExcluirNem tem erro nas contas rs
ResponderExcluirObs:Irônia
2° questão esta errado
ResponderExcluirno site http://www.estudegratis.com.br também tem Questões de Concurso grátis
ResponderExcluira primeira questão deveria dar a função já com os parênteses, a falta dele faz agnt multiplicar a fração com o 1000 primeiro, o que resulta numa resposta incoerente
ResponderExcluir