Aqui vai uma lista de questões sobre determinantes para que você se prepare para o vestibular.
01. (Unicamp - SP) Seja a um número real e seja:
a) Para a=1, encontre todas as raízes da equação p(x)=0
b) Encontre os valores de a para os quais a equação p(x)=0 tem uma única raiz real.
Solução:
a) Façamos o determinante com o valor de a = 1:
.jpg)
Temos o produto de duas parcelas igual a zero, então teremos duas situações:
3 - x = 0 ou (1 - x) 2 + 4 = 0
Na primeira temos que x = 3; na segunda não é possível determinar uma solução.
Logo, temos apenas uma raiz possível quando a for igual a 1.
b)
.jpg)
Novamente teremos duas situações: uma onde x=3 e a outra temos que determinar para quais valores de a teremos apenas a solução x = 3:
Para que só exista uma única raiz, essa equação do segundo grau não deve ter raiz, ou seja, seu discriminante deve ser menor que zero.
03. (TFC SFC 2001) Um sistema de equações lineares é chamado “possível” ou “compatível” quando admite pelo menos uma solução, e é chamado de “determinado” quando a solução for única e de “indeterminado” quando houver infinitas soluções. A partir do sistema formado pelas equações, X - Y = 2 e 2X + WY = Z, pode-se afirmar que se W = -2 e Z = 4, então o sistema é:
a) impossível e determinado
b) impossível ou determinado
c) impossível e indeterminado
d) possível e determinado
e) possível e indeterminado
O enunciado fornece duas equações: 1ª) X – Y = 2 2ª) 2X + WY = Z
Se substituirmos os valores de W=-2 e de Z=4 na segunda equação, obteremos: 2ª) 2X – 2Y = 4
O sistema linear formado pelas duas equações é o seguinte:
Passemos a construir a matriz de x, de y e a matriz incompleta, e também calcular os seus determinantes.
12 Æ determinante = 2 x (-2) – 4 x (-1) = 0
21 Æ determinante = 1 x 4 – 2 x 2 = 0
| x = | determinante da matriz de x___ = 0 = infinitos valores (indeterminado) |
| determinante da matriz incompleta | 0 |
| y = | determinante da matriz de y___ = 0 = infinitos valores (indeterminado) |
| determinante da matriz incompleta | 0 |
Obtidos os determinantes, já temos condições de obter os valores das incógnitas:
Resposta: existem infinitos pares (x,y) que são soluções! Æ Sistema Possível e Indeterminado.
a) duas linhas proporcionais;
b) duas colunas proporcionais;
c) elementos negativos;
d) uma fila combinação linear das outras duas filas paralelas;
e) duas filas paralelas iguais.
5) (U.F. Ouro Preto – MG) Considere a matriz:
Solução:
Ao resolver esta desigualdade obteremos o seguinte conjunto solução:
Ao resolver esta desigualdade obteremos o seguinte conjunto solução:
06 . Determine o valor de x para que o determinante da matriz A seja igual a 8.
Solução:
.jpg)
Ou seja, temos dois valores para x que fazem com que o determinante da matriz A seja igual a 8.
07. Sabe-se que Ax² + 2Bxy + Cy² + 2Dx + 2Ey + F, com A, B, C, D, E e F reais, fatora-se, no conjunto dos reais, em dois fatores de primeiro grau em x e y se, e somente se, B² - AC = 0 e o determinante da matriz, representada a seguir, for nulo. (imagem abaixo)
Com base nessas informações, DETERMINE m para que o polinômio x² + 2mxy - y² + x + y seja um produto de dois fatores de primeiro grau em x e y.
Com base nessas informações, DETERMINE m para que o polinômio x² + 2mxy - y² + x + y seja um produto de dois fatores de primeiro grau em x e y.
08. (Unicap - PE) Calcule o valor de x, a fim de que o determinante da matriz A seja nulo.
09. Seja a matriz quadrada M de ordem 3 cada elemento aij = i + j. O cofator do elemento a32 é :
a) -2 b) 0 c) 2 d) 5 e) 7
10. A é uma matriz quadrada de ordem 2, inversível, e det (A) o seu determinante. Se det (2A) = det (A*A), então det(A) será igual a:
a) 0 b) 1 c) 1/2 d) 4 e) 16
11. (FGVRJ-03) A organização econômica Merco é formada pelos países 1, 2 e 3. O volume anual de negócios realizados entre os três parceiros é representado em uma matriz A, com 3 linhas e 3 colunas, na qual o elemento da linha i e coluna j informa quanto o país i exportou para o país j, em bilhões de dólares.
então o país que mais exportou e o que mais importou no Merco foram, respectivamente:
a) 1 e 1 b) 2 e 2 c) 2 e 3 d) 3 e 1 e) 3 e 2
12) (UNITAU) O valor do determinante (imagem abaixo)
como produto de 3 fatores é:
como produto de 3 fatores é:
a) abc.
b) a (b + c) c.
c) a (a - b) (b - c).
d) (a + c) (a - b) c.
e) (a + b) (b + c) (a + c).
b) a (b + c) c.
c) a (a - b) (b - c).
d) (a + c) (a - b) c.
e) (a + b) (b + c) (a + c).
13) (UNESP) Se a e b são as raízes da equação a seguir: (imagem abaixo)
onde x > 0, então a + b é igual a:
a) 2/3
b) 3/4
c) 3/2
d) 4/3
e) 4/5
b) 3/4
c) 3/2
d) 4/3
e) 4/5
14) (UEL) A soma dos determinantes indicados a seguir é igual a zero (imagem abaixo)
a) quaisquer que sejam os valores reais de a e de b
b) se e somente se a = b
c) se e somente se a = - b
d) se e somente se a = 0
e) se e somente se a = b = 1
b) se e somente se a = b
c) se e somente se a = - b
d) se e somente se a = 0
e) se e somente se a = b = 1
15) (UECE) Se o determinante da matriz A, mostrada na figura adiante, é igual a 34 e o determinante da matriz B é igual a -34, então n-n‚ é igual a: (imagem abaixo)
a) 4
b) 5
c) 6
d) 7
a) 1/6
b) 1/3
c) 1/54
d) 1/15
e) 1/30
b) 5
c) 6
d) 7
16) Na função real definida na figura a seguir, (imagem abaixo) f (0,001) vale:
a) 0,02
b) 10001
c) 10²
d) 5001
e) 0,5
b) 10001
c) 10²
d) 5001
e) 0,5
17) (UECE) Sejam m e m‚ números reais positivos. Se o determinante da matriz A na figura adiante é v2/2, então o determinante da matriz B é: (imagem abaixo)
a) 9/4
b) 9/2
c) 25/4
d) 25/2
b) 9/2
c) 25/4
d) 25/2
18) (PUC-MG) M é uma matriz quadrada de ordem 3, e seu determinante é det(M)=2. O valor da expressão det(M)+det(2M)+det(3M) é:
a) 12
b) 15
c) 36
d) 54
e) 72
19) (UNIRIO) O valor de (imagem abaixo)
é igual a:
a) 0
b) 4(y + 3z)
c) 4(3x + y + 3z)
d) 4x + 2y + 3z
e) 12(x + z)
a) para quaisquer valores de a e b
b) apenas se a = 0
c) apenas se b = 0
d) somente se a = b
e) somente quando 1 + 2a + (b + 3) = 0
b) 4(y + 3z)
c) 4(3x + y + 3z)
d) 4x + 2y + 3z
e) 12(x + z)
20) O determinante da matriz mostrada na figura a seguir é nulo (imagem abaixo)
b) apenas se a = 0
c) apenas se b = 0
d) somente se a = b
e) somente quando 1 + 2a + (b + 3) = 0
21) (MACKENZIE) Dada a matriz mostrada na figura a seguir (imagem abaixo) , então o determinante da inversa de M vale:
b) 1/3
c) 1/54
d) 1/15
e) 1/30
22) (UNIOESTE) O valor de "a" para o qual o determinante adiante se anula é:
a) 1
b) 2
c) 3
d) 4
e) 5
det = 136
det = 17 . 8
é divisível por 17
Descubra como é possível conseguir falar com excelente fluência, rapidez e facilidade sem ter que ficar se matriculando em curso e comprando aqueles livros importados e caríssimos?
E aproveite as Ferramentas de estudo.
Um jeito mais fácil de treinar sua escuta e sua fala em inglês.
Como melhorar sua conversação rapidamente.
Como aprender a falar e entender sem ficar estudando gramática.
Inglês para negócios e áreas especificas.
Vamos ensinar-lhe alguns truques que passamos para os nossos alunos para atingir um alto nível de fluência em inglês. O vocabulário deste curso inclui vários grupos, entre eles: datas, meses, horas, cores, objetos comuns, roupas, família, pessoas, lugares, países, comida e compras etc.
23) (PUC-MG) Sendo D o determinante da matriz mostrada na figura adiante (imagem abaixo) o valor positivo de x é:
a) um múltiplo de 4.
b) um divisor de 10.
c) o mínimo múltiplo comum de 3 e 5.
d) o máximo divisor comum de 6 e 9.
b) um divisor de 10.
c) o mínimo múltiplo comum de 3 e 5.
d) o máximo divisor comum de 6 e 9.
24) (PUC-PR) O valor de x no determinante: (imagem abaixo)
b) 2
c) 3
d) 4
e) 5
25) (UEL-PR) O determinante mostrado na figura a seguir (imagem abaixo)
é positivo sempre que
a) x > 0
b) x > 1
c) x < 1
d) x < 3
e) x > -3
b) x > 1
c) x < 1
d) x < 3
e) x > -3
26) (UERJ) Os números 204, 782 e 255 são divisíveis por 17. Considere o determinante de ordem 3 abaixo: (imagem abaixo)
Demonstre que esse determinante é divisível por 17.
Demonstre que esse determinante é divisível por 17.
27) (ITA-SP) Sendo A, B e C matrizes reais de ordem n, considere as afirmações:
1) A(BC) = (AB)C
2) AB = BA
3) A+B = B+A
4) det (AB) = det (A) . det (B)
5) det (A+B) = det (A) + det (B)
Então, podemos afirmar que:
a) 1 e 2 estão corretas.
b) 2 e 3 estão corretas.
c) 3 e 4 estão corretas.
d) 4 e 5 estão corretas.
e) 5 e 1 estão corretas.
Solução:
1) Falso, pois em matrizes não podemos fazer a distributiva, como nos números, devemos realizar os produtos que estão indicados entre parênteses, o que não resulta valores iguais.
2) Falso, estamos falando em matrizes, precisamos esquecer os números, sabemos que isso até pode acontecer, mas em casos especiais, geralmente AB é diferente de BA.
3) Verdadeiro, pois a soma é realizada operando-se com os termos correspondentes em cada matriz, onde a ordem não interfere, veja:
3 + (-1) = 2 é o mesmo que (-1) + 3 = 2
4) Verdadeiro, vimos no Teorema de Binet.
5) Falso, lembre-se do alerta na videoaula, não confundir com o Teorema de Binet!!!
Letra C.
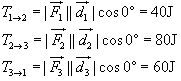
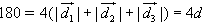
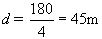
1) A(BC) = (AB)C
2) AB = BA
3) A+B = B+A
4) det (AB) = det (A) . det (B)
5) det (A+B) = det (A) + det (B)
Então, podemos afirmar que:
a) 1 e 2 estão corretas.
b) 2 e 3 estão corretas.
c) 3 e 4 estão corretas.
d) 4 e 5 estão corretas.
e) 5 e 1 estão corretas.
Solução:
1) Falso, pois em matrizes não podemos fazer a distributiva, como nos números, devemos realizar os produtos que estão indicados entre parênteses, o que não resulta valores iguais.
2) Falso, estamos falando em matrizes, precisamos esquecer os números, sabemos que isso até pode acontecer, mas em casos especiais, geralmente AB é diferente de BA.
3) Verdadeiro, pois a soma é realizada operando-se com os termos correspondentes em cada matriz, onde a ordem não interfere, veja:
3 + (-1) = 2 é o mesmo que (-1) + 3 = 2
4) Verdadeiro, vimos no Teorema de Binet.
5) Falso, lembre-se do alerta na videoaula, não confundir com o Teorema de Binet!!!
Letra C.
28) (UERJ) Em um supermercado, um cliente empurra seu carrinho de compras passando pelos setores 1, 2 e 3, com uma força de módulo constante de 4 newtons, na mesma direção e mesmo sentido dos deslocamentos.
Na matriz A abaixo, cada elemento aij indica, em joules, o trabalho da força que o cliente faz para deslocar o carrinho do setor i para o setor j, sendo i e j elementos do conjunto {1, 2, 3}.
Ao se deslocar do setor 1 ao 2, do setor 2 ao 3 e, por fim, retornar ao setor 1, a trajetória do cliente descreve o perímetro de um triângulo.
Nessas condições, o cliente percorreu, em metros, a distância de:
(A) 35
(B) 40
(C) 45
(D) 50
Solução:
Cada elemento aij da matriz A representa o trabalho realizado por uma força para deslocar o carrinho do setor ipara o setor j.
Como os vetores que representam a força exercida sobre o carrinho e o respectivo deslocamento são paralelos e de mesmo sentido, o trabalho em cada trecho é dado por:
Como os vetores que representam a força exercida sobre o carrinho e o respectivo deslocamento são paralelos e de mesmo sentido, o trabalho em cada trecho é dado por:
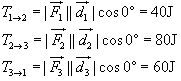
Uma vez que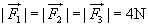 
, o trabalho total é igual a:
, o trabalho total é igual a:
Portanto, a distância total d percorrida pelo cliente é:
Letra C.
Gabarito:
4) D 5) 7) m = 0 8) x = 13 9) B 10) D 11) C
7) m = 0 8) x = 13 9) B 10) D 11) C
12) C 13) C 14) A 15) A 16) D 17) D 18) E 19) A 20) A 21) C 22) 64 23) D 24) B
25) B 26) det = 80 + 140 - 64 - 20det = 136
det = 17 . 8
é divisível por 17
27) C 28) C
Mais questões resolvidas: http://www.csajaboticabal.org.br/
Curso de Inglês Download - ONELAND Rápido
Vamos ensinar-lhe alguns truques que passamos para os nossos alunos para atingir um alto nível de fluência em inglês.
Metodologia Comunicativa
Descubra como é possível conseguir falar com excelente fluência, rapidez e facilidade sem ter que ficar se matriculando em curso e comprando aqueles livros importados e caríssimos?E aproveite as Ferramentas de estudo.
Professores Nativos
Um jeito mais fácil de treinar sua escuta e sua fala em inglês.Como melhorar sua conversação rapidamente.
Como aprender a falar e entender sem ficar estudando gramática.
Inglês para negócios e áreas especificas.
Diferenciais ONELAND.
Vamos ensinar-lhe alguns truques que passamos para os nossos alunos para atingir um alto nível de fluência em inglês. O vocabulário deste curso inclui vários grupos, entre eles: datas, meses, horas, cores, objetos comuns, roupas, família, pessoas, lugares, países, comida e compras etc.
Nenhum comentário:
Postar um comentário