Determinante de uma matriz quadrada de 1ª ordem
O determinante da matriz A = | a11|, indicado por det A ou |a11|, é o próprio elemento a11, ou seja:
det A = |a11| = a11 (não confundir com o módulo do número a11).
Exs: Se A = [-3], então det A = |-3|.
Se B = [6], então det A = |6| = 6
Determinante de uma matriz quadrada de 2ª ordem
O determinante da matriz
 é igual à diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária.
é igual à diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária.Veja o exemplo abaixo:
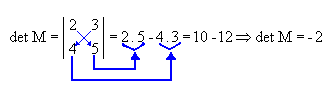
Determinante de uma matriz de 3ª ordem
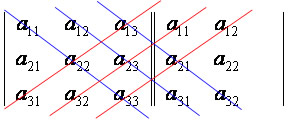
O cálculo do determinante de uma matriz quadrada de ordem 3 pode ser calculado usando a regra de Saurus, que consiste no seguinte:
- copia-se o determinante repetindo-se as duas primeiras colunas;
- multiplicam-se os elementos ligados por "traços vermelhos", mantendo-se o sinal de cada produto;
- multiplicam-se os elementos ligados por "traços azuis", trocando-se o sinal de cada produto;
- somam-se os resultados obtidos.
Diagonal principal
(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)
Diagonal secundária
(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21 * a33)
Determinante
D = {(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)} – {(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21* a33)}
(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)
Diagonal secundária
(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21 * a33)
Determinante
D = {(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)} – {(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21* a33)}
Exemplo :
Dada a matriz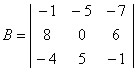 , calcule o seu determinante.
, calcule o seu determinante.
Diagonais principais
(–1) * 0 * (–1) = 0
(–5) * 6 * (–4) = 120
(–7) * (8) * (5) = – 280
0 + 120 + (–280)
120 – 280
– 160
Diagonais secundárias
(–7) * 0 * (–4) = 0
(–1) * 6 * 5 = – 30
(–5) * 8 * (–1) = 40
0 + (–30) + 40
–30 +40
10
Determinante
DB = –160 – 10
DB = – 170
Dada a matriz
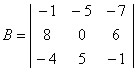 , calcule o seu determinante.
, calcule o seu determinante.Diagonais principais
(–1) * 0 * (–1) = 0
(–5) * 6 * (–4) = 120
(–7) * (8) * (5) = – 280
0 + 120 + (–280)
120 – 280
– 160
Diagonais secundárias
(–7) * 0 * (–4) = 0
(–1) * 6 * 5 = – 30
(–5) * 8 * (–1) = 40
0 + (–30) + 40
–30 +40
10
Determinante
DB = –160 – 10
DB = – 170
Matriz Cofator
consideremos uma matriz quadrada A, de ordem n(n ≥ 2), e um elemento aij de A. Chama-se cofator do elemento aij ao produto de (-1)i+j pelo determinante da matriz obtida, quando se elimina em A a linha i e a coluna j.
Exemplo:
 , vamos calcular os cofatores A22, A23 e A31:
, vamos calcular os cofatores A22, A23 e A31: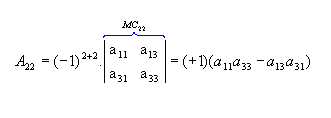 |
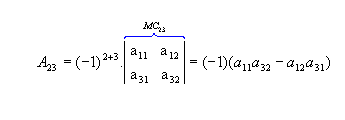 |
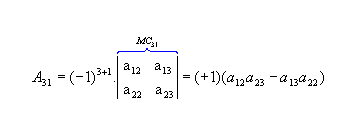 |
Nenhum comentário:
Postar um comentário