implicações e equivalências lógicas exercícios

 Artigo sobre implicações e equivalências lógicas com exercícios para uma melhor compreensão do assunto.

Uma proposição P implica na proposição Q se e somente se a tabela verdade de P ® Q for uma uma tautologia.

O símbolo P ⇒ Q (P implica Q) representa a implicação lógica.          A implicação lógica goza das seguintes propriedades: P1 – Reflexiva. Isto é P Þ P. P2 – Transitividade. Isto é P Þ Q e Q Þ S então P Þ S.       A transitividade pode ser estendida a qualquer série de proposições: P Þ R e R Þ S e S Þ ...Þ X então P Þ X. Estão abaixo as implicações lógicas fundamentais: p => p v q          p ^ q => p (p v q) ^ ~p => q  (p → q) ^ p => q        (Modus ponens) (p → q) ^ ~q => ~p    (Modus tollens) (p → q) ^ (q → r) => p → r    (Silogismo hipotético) p ↔ q => p →q  p ↔ q => q →p (p↔q) ^ p => q As implicações que estão destacadas em vermelho são as mais importantes regras de inferência, e as que mais aparecem em questões de concurso. No mais, apenas grave: a implicação (=>) para fins de cálculo lógico, corresponde a condicional (→). Equivalência lógica  Há equivalência entre as proposições P e Q quando tiverem a mesma tabela-verdade ou  quando a bicondicional P ↔ Q for uma tautologia. P ⇔ Q (P é equivalente a Q) é o símbolo que representa a equivalência lógica.          Para exemplificar, tomemos as seguintes proposições (p → q) ↔ (~q → ~p) criando suas tabelas-verdades. 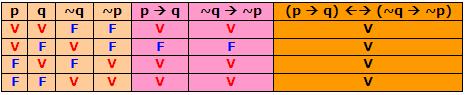Portanto, p → q é equivalente a ~q → ~p, pois estas proposições possuem a mesma tabela-verdade ou a bicondicional (p → q) ↔ (~q → ~p) é uma tautologia. Equivalências lógicas válidas: ~~p <=> p          (dupla negação) ~p → p <=> p     (Clavius) p →q <=> ~p v q p ↔ q <=> (p → q) ^ (q →p) p ↔ q <=> (p ^ q) v (~p ^ ~q) p → q <=> ~q → ~p p → p ^ q <=> p → q      (absorção) p ^ ~q → c <=> p → q p ^ q → r <=> p → (q → r)   (exportação-importação) Destacadas em vermelho, as equivalências lógicas mais usadas em resoluções de questões. Uma diferença importantíssima entre a implicação e equivalência reside no fato de que, na implicação, só há o caminho de ida, não existe o de volta. Ou melhor, toda equivalência é uma implicação lógica por natureza. Diferentemente, a implicação não se trata necessariamente de uma equivalência lógica. Podemos então dizer que toda equivalência é uma implicação lógica, mas nem toda implicação é uma equivalência lógica. Assim: p ^ q => p (certo) O caminho de volta pode estar errado se desejado: p => p ^ q (errado) Na equivalência, pode-se ir e vir entre duas proposições. Temos: (~p v q) <=> (p → q) O caminho de volta seria perfeitamente válido: (~p v q) <=> (p → q) Em outras palavras:dizer que p ^ q <=> p é a mesma coisa que afirmar que p ^ q => p. Porém p ^ q => p não é a mesma coisa de dizer que p <=> p ^ q QUESTÕES 1) (FCC TCE-MG 2007) São dadas as seguintes proposições: I. Se Jaime trabalha no Tribunal de Contas, então ele é eficiente. II. Se Jaime não trabalha no Tribunal de Contas, então ele não é eficiente. III. Não é verdade que Jaime trabalha no Tribunal de Contas e não é eficiente. IV. Jaime é eficiente ou não trabalha no Tribunal de Contas. É correto afirmar que são logicamente equivalentes apenas as proposições de números: a) 2 e 4 b) 2 e 3 c) 2, 3 e 4 d) 1, 2 e 3 e) 1, 3 e 4 **gabarito** ------------------  resolução: Simplificamos primeiro as proposições: I) Trabalha --> eficiente II) ~Trabalha --> ~eficiente III) ~(trabalha ^ ~eficiente) IV) eficiente v ~trabalha Agora buscamos as equivalências lógicas. I) Trabalha --> eficiente é equivalente a essas duas: ~eficiente --> ~Trabalha ~trabalha v eficiente II) ~Trabalha --> ~eficiente é equivalente a essas duas: eficiente --> trabalha trabalha v ~eficiente III) ~(trabalha ^ ~eficiente) é equivalente a: ~trabalha v eficiente (a negação de p ^ q é ~p v ~q) IV) eficiente v ~trabalha é equivalente a essas duas: ~eficiente --> ~trabalha trabalha --> eficiente em cores, todas as equivalências em comum.  letra E, a correta. 2) (FGV/2018) Considere a sentença “Joana gosta de leite e não gosta de café”. Sabe-se que a sentença dada é falsa. Deduz-se que: a) Joana não gosta de leite e não gosta de café; b) Se Joana gosta de leite, então ela não gosta de café; c) Joana gosta de leite ou gosta de café; d) Se Joana não gosta de café, então ela não gosta de leite; e) Joana não gosta de leite ou não gosta de café. Resolução: Primeiro negamos: Joana gosta de leite e não gosta de café Logo: Joana não gosta de leite OU gosta de café. Não encontramos essa alternativa, então vamos para a equivalência. ==> Na equivalência da disjunção, para ''virar'' condicional, devemos NEGAR a primeira e manter a segunda. Logo: Se Joana gosta de leite, então gosta de café. Novamente, não encontramos essa alternativa, então devemos tentar encontrar a equivalência da alternativa. As triviais de equivalência da condicional são com ''ou'' (nega a 1ª V mantém segunda) ou a contrapositiva. Já vimos que com ''OU'' não consta, então só pode ser a contrapositiva. Logo: Se Joana não gosta de café, então não gosta de leite. Alternativa “d”. 3) (VUNESP/2018 – Investigador de Polícia) Considere a afirmação: Se João calçou as botas, então ele não escorregou. A alternativa que contém uma afirmação equivalente é: a) Se João não escorregou, então ele calçou as botas. b) João calçou as botas e não escorregou. c) Se João calçou as botas, então ele escorregou. d) João não calçou as botas ou ele não escorregou. e) João calçou as botas ou ele não escorregou.   Resolução: Troca o Se...Então por OU e nega a 1ª e mantém a 2ª. Assim: João NÃO calçou as botas OU ele não escorregou. Alternativa “d”. 4) Mostrar que as proposições “x = 1 v x ³ 3” e “~(x < 3 ^ x = 1)” não são equivalentes. 5) Demonstre as relações abaixo utilizando as tabelas-verdade: a)    p ® q Ù r  Û  ( p ® q ) Ù ( p ® r ) b)    p ® q Ú r Û ( p ® q ) Ú ( p ® r ) c)    p Ù q ® r Û p ® ( q ® r ) d)    ~( ~p ® ~q ) Û ~p Ù q e)    ~( p Ù q Ù r ) Û ~p Ú ~q Ú ~r f)      ~( p Ú q Ú  r ) Û ~p Ù ~q Ù ~r