Nesse artigo estudaremos introdução à probabilidade, espaço amostral, probabilidade de ocorrer um evento e probabilidade da união de dois eventos com exemplos resolvidos.
1. Introdução
2. Espaço amostral
Um experimento que pode apresentar resultados diferentes, quando repetido nas mesmas condições, é chamado experimento aleatório.
Chamamos espaço amostral ao conjunto de todos os resultados possíveis de um experimento aleatório. Dizemos que um espaço amostral é equiprovável quando seus elementos têm a mesma chance ocorrer.
Representamos um espaço amostral, ou espaço amostral universal como também é chamado, pela letra S. No caso da moeda representamos o seu espaço amostral por:
S = { cara, coroa }
Se novamente ao invés de uma moeda, o objeto a ser lançado for um dado, o espaço amostral será:
S = { 1, 2, 3, 4, 5, 6 }
Observação: O número de elementos de um espaço amostral pode, muitas vezes, ser calculado utilizando-se conceitos da análise combinatória.
Exemplo:
Determinar o número de elementos do espaço amostral relativo à escolha de um número de 3 algarismos distintos, formados a partir dos algarismos 2, 3, 4, 5, 6 e 7.
Solução:
O problema fica resolvido calculando-se o número de arranjos simples de 6 elementos tomados 3 a 3, isto é: n(S) = A6,3 = 6 . 5 . 4 = 120
Chama-se evento a qualquer subconjunto de um espaço amostral. Considerando o lançamento de um dado e a leitura dos pontos da face superior, temos o espaço amostral S = {1, 2, 3, 4, 5, 6}.
Um exemplo de evento é " sair um número menor que 4". Indicando esse evento por A, temos: A = {1, 2, 3}
3. Probabilidade de ocorrer um evento
Em um experimento aleatório, onde S é um espaço equiprovável, a probabilidade de ocorrer um evento qualquer E é o número p(E), dado por:
p(E) = n (E) / n(S)
Observação: se E = Ø, então p(E) = 0 e se E = S, então p(E) = 1. Com isso fica eveidente que a probabilidade de ocorrer um evento qualquer E é no mínimo igual a zero e no máximo igual a 1, ou seja: 0 ≤ p(E) ≤ 1.
Exemplo:
Antes do início de um jogo de futebol, o juiz sorteia, entre os capitães, o lado em que cada time irá jogar. Para isso, lança uma moeda para o ar e verifica, ao cair, se deu "cara" ou "coroa". O capitão de um dos times escolhe "cara". Determine a probabilidade de ser esse jogador a escolher o lado do campo.
Solução:
S = {cara, coroa} e n(S) = 2
E = {cara} e n(E) = 1
p(E) = n(E) / n(s) = 1/2
Observação: é bastante comum representar uma probabilidade na forma de porcentagem.
No exemplo dado temos: p(E) = 1/2 = 50/100 = 50%
4. Probabilidade da união de dois eventos
Consideremos dois eventos A e B de um mesmo espaço amostral S. da teoria sabemos que:
n(AUB) = n(A) + n(B) - n(A ∩ B)
Dividindo todos os membros da igualdade acima por n(S), temos:
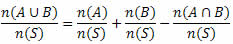 ► p(A U B) = p(A) + p(B) - p(A ∩ B)
► p(A U B) = p(A) + p(B) - p(A ∩ B)
A probabilidade da união de dois eventos A e B é igual à soma da probabilidades desses eventos, menos a probabilidade da intersecção de A com B.
Observação: se A e B forem disjuntos, isto é, se A ∩ B = Ø, então p(A U B) = p(A) + p(B)
Vejamos alguns exemplos:
Exemplo 1:
No lançamento de um dado, qual é a probabilidade de se obter o número 4 ou um número par?
Solução:
O espaço amostral é:
S = {1, 2, 3, 4, 5, 6}, onde n(S) = 6.
O evento "número 4" é A = |4|, onde n(A) = 1.
O evento "número par" é B = |2, 4, 6|, onde n(B) = 3
A ∩ B = |4| ∩ |2, 4, 6| = |4|. Então n(A ∩ B) = 1.
Assim temos:
p(A U B) = p(A) + P(B) - p(A ∩ B) ► p(A U B) = 1/6 + 1/3 - 1/6
Logo, p(A U B) = 1/2 ou 50%.
Exemplo 2:
Sorteado um número natural de 1 a 22, qual a probabilidade de se obter um número de 1 algarismo ou um múltiplo de 10?
Solução:
Temos: n(S) = 22.
O evento "número de 1 algarismo" é A = {1, 2,..., 9} e n(A) = 9.
O evento "múltiplo de 10" é B = |10, 20| e n(B) = 2.
Como A ∩ B = Ø, então:
p(A U B) = p(A) + p(B) ► p(A U B) = 9/22 + 2/22 = 11/22 = 0,5 ou 50%.
4. Probabilidade da união de dois eventos
Consideremos dois eventos A e B de um mesmo espaço amostral S. da teoria sabemos que:
n(AUB) = n(A) + n(B) - n(A ∩ B)
Dividindo todos os membros da igualdade acima por n(S), temos:
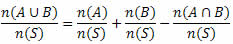 ► p(A U B) = p(A) + p(B) - p(A ∩ B)
► p(A U B) = p(A) + p(B) - p(A ∩ B) A probabilidade da união de dois eventos A e B é igual à soma da probabilidades desses eventos, menos a probabilidade da intersecção de A com B.
Observação: se A e B forem disjuntos, isto é, se A ∩ B = Ø, então p(A U B) = p(A) + p(B)
Vejamos alguns exemplos:
Exemplo 1:
No lançamento de um dado, qual é a probabilidade de se obter o número 4 ou um número par?
Solução:
O espaço amostral é:
S = {1, 2, 3, 4, 5, 6}, onde n(S) = 6.
O evento "número 4" é A = |4|, onde n(A) = 1.
O evento "número par" é B = |2, 4, 6|, onde n(B) = 3
A ∩ B = |4| ∩ |2, 4, 6| = |4|. Então n(A ∩ B) = 1.
Assim temos:
p(A U B) = p(A) + P(B) - p(A ∩ B) ► p(A U B) = 1/6 + 1/3 - 1/6
Logo, p(A U B) = 1/2 ou 50%.
Exemplo 2:
Sorteado um número natural de 1 a 22, qual a probabilidade de se obter um número de 1 algarismo ou um múltiplo de 10?
Solução:
Temos: n(S) = 22.
O evento "número de 1 algarismo" é A = {1, 2,..., 9} e n(A) = 9.
O evento "múltiplo de 10" é B = |10, 20| e n(B) = 2.
Como A ∩ B = Ø, então:
p(A U B) = p(A) + p(B) ► p(A U B) = 9/22 + 2/22 = 11/22 = 0,5 ou 50%.
Nenhum comentário:
Postar um comentário