Ao estudarmos
as inequações logarítmicas, devemos ter cuidados especiais com as restrições a
que devem estar submetidas a incógnita.
Para resolvê-las, procuraremos obter nos dois membros logaritmos de
mesma base. A partir disso, trabalharemos apenas com os
logaritmandos, usando o fato de a função ser crescente ou decrescente:
a) mantendo para eles o mesmo sinal da
inequação quando a base for maior que 1, pois a função é crescente;
b) invertendo para eles o sinal da inequação
quando a base estiver entre 0 e 1, pois a função é decrescente.
Ex: Resolver a inequação log2 x - 1 >
5.
Temos que
→ log2 x - 1
> log2 2
Como a base é 2 > 1, a função logarítmica
é crescente e, portanto, o sinal > da inequação deve ser mantido para os
logaritmandos, ou seja, devemos ter x – 1 > 32.
Então, x > 32 + 1 → x > 33 ( I )
A solução é o conjunto dos valores de x que, além de tornar ( I ) verdadeiro,
satisfazem também a restrição inicial.
Desse modo, a restrição deverá ser “ mais
trabalhada”, ou seja: x – 1 > 0 → x > 1 ( II )
O conjunto solução é S = {x Є R/x > 33}.
Ex2: O número real x que satisfaz a equação log2(12 – 2x) = 2x é:
Solução:
log2(12 – 2x) = 2x
12 – 2 = 22x
22x + 2x – 12 = 0
(2x)2 + 2x – 12 = 0
Substituindo 2x por y, temos:
y2 + y – 12 = 0
Resolvendo a equação do 2.º grau acima,
temos:
y’
= -4 ; y’’ = 3
2x = -4
2x = 3
x = log23
Exercícios inequações logarítmicas
1) Resolva a inequação log3 (2 – 5x) ≤ log3 3
2) Resolva a inequação logarítmica 
3) Determine
para quais valores de x o número logx+1 (2 - x)
4) (Unicamp) Suponha que o preço de um automóvel tenha uma desvalorização de 19% ao ano sobre o preço do ano anterior. Se F representa o preço inicial (preço de fábrica) e p(t) o preço após t anos, pede-se:
a) A expressão para p(t)
b) O tempo mínimo necessário, em número inteiro de anos, após a saída da fábrica, para que um automóvel venha a valer menos que 5% do valor inicial. Se necessário, use:
log2 = 0,301 log3 = 0,477
5) (Fuvest) Seja f(x) o logaritmo de 2x na base 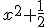 .
.
Resolva a inequação f(x) > 1.
1) S = { x
Є R/ -1/5 ≤ x < 2/5} 2)
Resolva a inequação f(x) > 1.
Gabarito:
1) S = { x
Є R/ -1/5 ≤ x < 2/5} 2)  3) S = { x ∈ R/ -1 < x < 2 e x ≠ 0}
3) S = { x ∈ R/ -1 < x < 2 e x ≠ 0}
4) a) p(t) = (0,81)t F b) t = 15 anos 5) S= {x 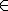 R | 0 < x <
R | 0 < x < 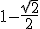 ou
ou 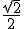 < x <
< x < 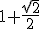 }
}
Ai do nada da 32 na letra b da 1° , da pra explicar?
ResponderExcluir2^5=32
Excluir