exercícios resolvidos Tautologia

Artigo sobre tautologia, contradição e contingência teoria e exercícios resolvidos

Sentenças moleculares que são sempre verdadeiras, independentemente do valor lógico das proposições que a constituem, são chamadas tautologias.

Exemplo:

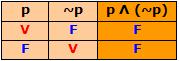
A proposição p ∨ (~p) é uma tautologia, pois o seu valor lógico é sempre V, conforme a tabela-verdade. 

Exemplo:

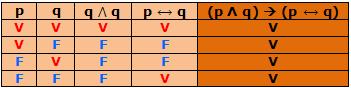
A proposição (p Λ q) → (p → q) é uma tautologia, pois a última coluna da tabela-verdade só possui V. 

Exercícios resolvidos sobre tautologia 

1) (SEBRAE- 2010 - UNB/Cespe) Julgue o item subseqüente.

A proposição [¬B]∨{[¬B]→A} é uma tautologia.

Solução:

Certo. Primeiro é necessário construir a tabela-verdade dessa proposição.

A	B	¬B	[¬B]→A	[¬B]∨{[¬B]→A}
V	V	F	V	V
V	F	V	V	V
F	V	F	V	V
F	F	V	F	V

Uma vez que a última coluna da tabela acima contém somente o valor lógicos V, a proposição [¬B]∨{[¬B]→A} é uma tautologia.

2) (FT_98) Chama-se tautologia a toda proposição que é sempre verdadeira, independentemente da verdade dos termos que a compõem. Um exemplo de tautologia é:

a) se João é alto, então João é alto ou Guilherme é gordo

b) se João é alto, então João é alto e Guilherme é gordo

c) se João é alto ou Guilherme é gordo, então Guilherme é gordo

d) se João é alto ou Guilherme é gordo, então João é alto e Guilherme é gordo

e) se João é alto ou não é alto, então Guilherme é gordo

Solução:

________________________________________________________________________

Analisando a proposição se João é alto, então João é

alto ou Guilherme é gordo

Logo, essa proposição representa uma tautologia.

Alternativa: A

3) Considere as fórmulas:

I - (p v q) → p
II - (p ^ q) → p
III - (p ^ q) → (p V q)

É(São) tautologia(s) a(s) fórmula(s):


a)opção (A) I, somente.              b) opção (B) II, somente.

c) opção (C) III, somente.          d) opção (D) I e III, somente.
e) opção (E) I, II e III.

Contradição

Contradição é uma proposição cujo valor lógico é sempre falso.

Exemplo:

A proposição (p Λ q) Λ (p Λ q) é uma contradição, pois o seu valor lógico é sempre F conforme a tabela-verdade. Que significa que uma proposição não pode ser falsa e verdadeira ao mesmo tempo, isto é, o principio da não contradição.

Contingência 
Quando uma proposição não é tautológica nem contraválida, a chamamos de contingência ou proposição contingente ou proposição indeterminada.