Nesse artigo, estudaremos o triângulo de Pascal e suas propriedades com exercícios resolvidos
. Isto já era de se esperar, pois como vimos no estudo dos coeficientes binomiais, 
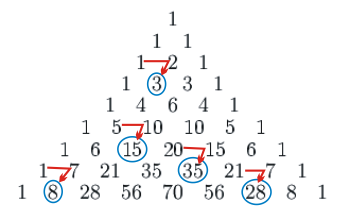
Basta efetuar os cálculos para chegar à figura inicial:
Reparando no Triângulo de Pascal acima, notamos que o número 15 pode ser obtido se somarmos o número que está na linha imediatamente acima ( 10 ) com o vizinho da esquerda deste número
( 5 ).
Veja que este raciocínio serve para todos os números do triângulo, com exceção do primeiro e do último número de cada linha.
Propriedades do Triângulo de Pascal
O triângulo de pascal possui várias propriedades. Citaremos as seguintes:
Primeira propriedade
Em uma mesma linha dois binomiais equidistantes dos extremos são iguais. Considere, como exemplo, a sétima linha:
1 7 21 35 35 21 7 1
Segunda propriedade
A soma de dois elementos consecutivos de uma mesma linha é igual ao elemento situado abaixo do segundo elemento somado.
Vamos verificar as somas apontadas na figura:
Observe que esta propriedade é a própria relação de Stifel.
Terceira propriedade
A soma dos elementos da linha de de numerador n é igual a 2n (2 elevado a n).
vejamos:
1 ► soma = 20 = 1
1 1 ► soma = 21 = 2
1 2 1 ► soma = 22 = 4
1 3 3 1 ► soma = 23 = 8
1 4 6 4 1 ► soma = 24 = 16
1 5 10 10 5 1 ► soma = 25 = 32
1 6 15 20 15 6 1 ► soma = 26 = 64
Vamos resolver os seguintes exercícios, aplicando as propriedades do triângulo de Pascal.
Exemplo 1:
Sendo 1 a 21 35 b c 7 1 uma linha do triângulo de Pascal, determinar a, b e c:
Solução:
1 a 21 35 b c 7 1
Pela 1ª propriedade, temos a = 7, b = 35 e c = 21.
Exemplo 2:
Sendo:
1 7 21 b 35 21 e 1
1 8 a 56 c d 28 8 1
duas linhas consecutivas do triângulo de Pascal, vamos determinar a, b, c, d, e.
De acordo com a 2ª propriedade, temos:
a = 7 + 21 = 28
21 + b = 56 ► b = 35
b + 35 = c ► c = 70
d = 35 + 21 = 56
21 + e = 28 ► e = 7
Calcular a soma:
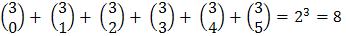
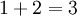
legal mesmo cara
ResponderExcluirAmei, me ajudou bastante.
ResponderExcluir