É fácil demonstrar as seguintes propriedades dos logaritmos, todas decorrentes da definição:
O logaritmo de um número b em uma base a é o expoente x que se deve aplicar à base a para se ter o número b. Dessa forma:
logab = x ↔ ax = b
Exemplos: log39 ↔ 32 = 9
log10100 ↔ 102 = 100
O logaritmo do número 1 em qualquer base sempre será igual a 0.
loga1 = 0, pois a0 = 1
O logaritmo de qualquer número a na própria base a será igual a 1.
logaa = 1, pois a1 = a
O logaritmo de uma potência da base é o expoente, em qualquer base.
logaam = m, pois m * logaa = m * 1 = m
A potência de base a e expoente logab é igual a b.
alogab = b, pois logab = x → ax = b
Dois logaritmos são iguais, quando seus logaritmandos forem iguais.
logab = logac ↔ b = c
Esta propriedade é muito utilizada na solução de exercícios envolvendo equações onde aparecem logaritmos (equações logarítmicas).
O logaritmo de um produto é igual a soma dos logaritmos dos fatores
loga(b.c) = log a b + log a b
Observe que
log2 (8.4) = log2 (32) = 5
log2 (8.4) = log2 (32) = 5
O logaritmo de um quociente é igual a subtração dos logaritmos do numerador e do denominador.
loga(b/c) = log a b - log a b
Observe que
log2 (8/4) = log2 (2) = 1
log2 (8/4) = log2 (2) = 1
O logaritmo de uma potência é igual a multiplicação do expoente pelo logaritmo da base.
loga(bc) = c. log a b
Observe que
log2 (25) = log2 (32) = 5
log2 (25) = log2 (32) = 5
Propriedade da mudança de base.
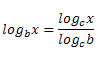
Exemplo: Se desejarmos calcular o valor do seguinte logaritmo log5
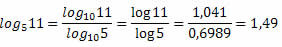
Os cálculos dos logaritmos, após a mudança de base, foram feitos com o auxílio de uma calculadora científica.
Exemplos:
a)logx8 = 2 → x2 = 8 → √x = √8 → x = 2√2
b)log4(2x – 1) = 1/2 → 2x – 1 = 41/2 → 2x – 1 = √4 → 2x – 1 = 2 → 2x = 3 → x = 3/2
b)log4(2x – 1) = 1/2 → 2x – 1 = 41/2 → 2x – 1 = √4 → 2x – 1 = 2 → 2x = 3 → x = 3/2
c) log81x = 3/4 → x = 813/4 → x = (34)3/4 → x = 312/4 → x = 33 → x = 27
d) 16log25 = (24)log25 = (2log25)4 = 54 = 625
e) log0,01 = x → 10x = 0,01 → 10x = 1/100 → 10x = 10–2 → x = –2
e) log0,01 = x → 10x = 0,01 → 10x = 1/100 → 10x = 10–2 → x = –2
f) log(1/100)=Log(10-2)=-2
Nenhum comentário:
Postar um comentário