Probabilidade condicional exemplos e conceito

Nesse artigo, vamos ver conceito e exemplos resolvidos de probabilidade condicional.

A probabilidade condicional é a probabilidade de ocorrência de um evento A, sabendo da ocorrência de outro evento B, ambos sendo eventos de um espaço amostral S finito. A ocorrência de A está condicionada ao fato de B já ter ocorrido, ou seja, a ocorrência do evento B interfere na do evento A.

A probabilidade de ocorrência de um evento A em relação a um evento ocorrido B é expressa como:

Para calculá-la podemos nos utilizar da fórmula:

Sabemos que 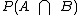, a probabilidade da intersecção, é a razão do seu número de elementos, para o número de elementos do espaço amostral:

A probabilidade de B também é a razão do seu número de elementos, para o número de elementos do espaço amostral:

Os substituindo na fórmula original temos:

Exemplo:

Em uma pesquisa realizada com 10.000 consumidores sobre a preferência da marca de sabão em pó, verificou-se que: 6500 utilizam a marca X; 5500 utilizam a marca Y; 2000 utilizam as duas marcas. Foi sorteada uma pessoa desse grupo e verificou-se que ela utiliza a marca X. Qual a probabilidade dessa pessoa ser também usuária da marca Y?

Solução: Vamos identificar cada um dos eventos.

A: Usuário da marca Y.
B: Usuário da marca X.

Queremos determinar P(A|B) e sabemos que o número de elementos do espaço amostral é n(S) = 10000.
Temos, também, que:

n(A∩B) = 2000

Segue que:

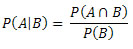
Mas

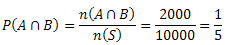
Da teoria de conjunto, temos que:

n(B) = 6500 – n(A∩B) = 6500 – 2000 = 4500

Assim, teremos:

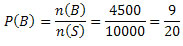
Logo,

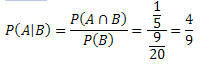
Observação: caso A e B sejam eventos independentes, a fórmula 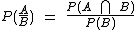 fica assim:

p(A ∩ B) = p(A) . p(B)

A relação acima pode ser generalizada para mais de dois eventos independentes.

Inversamente, caso p(A) . p(B) = p(A ∩ B), os eventos A e B são independentes.

A questão seguinte, adaptada da Fuvest, é um exemplo dessa situação:

Exemplo 1:
Considere o experimento que consiste no lançamento de um dado perfeito (todas as seis faces tem probabilidades iguais). Com relação a esse experimento, considere os seguintes eventos:

A: O resultado do lançamento é par.

B: O resultado do lançamento é  estritamente maior do que 4.

C: O resultado é múltiplo de 3.

a) A e B são eventos independentes?

Solução:

p(A) = 3/6 = 1/2, p(B) = 2/6 = 1/3 e p(A ∩ B) = 1/6

Como p(A) . p(B) = 1/2 . 1/3 = 1/6 e esse valor é igual a p(A ∩ B), concluímos que A e B são eventos independentes.

b) B e C são eventos independentes?

Solução:

p(B) = 2/6 = 1/3, P(C) = 2/6 = 1/3 e p(B ∩ C) = 1/6 

Como p(B) . p(C) = 1/3 . 1/3 = 1/9 e esse valor é diferente de p(B ∩ C), concluímos que B e C não são eventos independentes.

Exemplo 2:

Um dado é lançado três vezes, calcule a probabilidade de que o número 3 ocorra somente no primeiro e no terceiro lançamentos.

Solução:

Temos três eventos independentes, pois o fato de sair um determinado número num dos lançamentos não influi em nada no que possa ocorrer no lançamento seguinte.

• no primeiro lançamento deve ocorrer o número 3. A probabilidade de isso ocorrer é dada por:

                                                          P1 = 1/6

• no segundo lançamento deve ocorrer um dos números: 1, ou 2, ou 4, ou 5, ou 6. A probabilidade de isso ocorrer é dado por:

                                                         P2 = 5/6

• no terceiro lançamento deve ocorrer o número 3. A probabilidade de isso acontecer é dada por:

                                                         P3 = 1/6

Então, a probabilidade de sair o número 3 somente no primeiro e no terceiro lançamentos é dada por:

p = p1 . p2 . p3 = 1/6 . 5/6 . 1/6 = 5/256

Curso aqui mais detalhes http://aprendaadesenhardozero.com.br/cursoonline/…

Curso Online de Desenho — Aprenda a Desenhar do Zero

Ivan, estou feliz com o curso, sempre quis desenhar, mas o tempo e muito curto, e retomei esse sonho com o curso, aos poucos estou conseguindo cumprir todas as tarefas e vejo muitas melhorias nos meus trabalhos, Ivan suas explicações são...

APRENDAADESENHARDOZERO.COM.BR