Exercícios resolvidos e propostos com gabarito de arranjos simples para melhor fixação da parte teórica.
Exercícios Arranjos simples
Resolução:
Sabemos que 1 ano é composto de 12 meses, então devemos determinar o número de sequência através do arranjo de 12, tomados 6 a 6.

02. Em uma urna de sorteio de prêmios existem dez bolas enumeradas de 0 a 9. Determine o número de possibilidades existentes num sorteio cujo prêmio é formado por uma sequência de 6 algarismos.
Resolução:

03. Dos números distintos que são formados com todos os algarismos do número 333669, quantos desses são ímpares?
Resolução:
Nesta questão, número ímpares serão aqueles terminados em 3 ou 9.
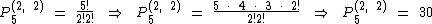
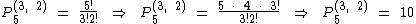
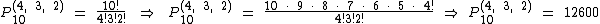
06. Em uma escola está sendo realizado um torneio de futebol de salão, no qual dez times estão participando. Quantos jogos podem ser realizados entre os times participantes em turno e returno?
07. Calcule o número de arranjos simples de 10 elementos tomados 3 a 3.

03. Dos números distintos que são formados com todos os algarismos do número 333669, quantos desses são ímpares?
Resolução:
Nesta questão, número ímpares serão aqueles terminados em 3 ou 9.
No caso dos números terminados em 3 devemos calcular P5(2, 2), pois um dos dígitos três será utilizado na última posição e dos 5 dígitos restantes, teremos 2 ocorrências do próprio algarismo 3 e 2 ocorrências do 6:
Agora no caso dos números terminados em 9 devemos calcular P5(3, 2), pois o dígito 9 será utilizado na última posição e dos 5 dígitos que sobram, teremos 3 ocorrências do 3 e 2 ocorrências do dígito 6:
Como temos 30 números terminados em 3 e mais 10 terminados em 9, então no total temos 40 números ímpares.
Logo:
Dos números formados, 40 deles são ímpares.
04. Possuo 4 bolas amarelas, 3 bolas vermelhas, 2 bolas azuis e 1 bola verde. Pretendo colocá-las em um tubo acrílico translúcido e incolor, onde elas ficarão umas sobre as outras na vertical. De quantas maneiras distintas eu poderei formar esta coluna de bolas?
Resolução:
Resolução:
Neste caso de permutação com elementos repetidos temos um total de 10 bolas de quatro cores diferentes. Segundo a repetição das cores, devemos calcular P10(4, 3, 2):
Então:
Eu poderei formar esta coluna de bolas de 12600 maneiras diferentes.
05. Em um torneio internacional de natação participaram cinco atletas europeus, dois americanos e um brasileiro.
05. Em um torneio internacional de natação participaram cinco atletas europeus, dois americanos e um brasileiro.
a) De quantos modos distintos poderão ser distribuídas as medalhas de ouro, prata e bronze?
São 8 atletas (5 europeus + 2 americanos + 1 brasileiro) que vão disputar as 3 posições do pódio e é claro que importa a ordem né (ouro, prata e bronze)
A 8,3 = 8!/(8-3)! = 8!/5! = 8×7x6x5!/5! = 8×7x6 = 336
Temos 336 maneiras diferentes de preencher este pódio.
b) Em quantos resultados só aparecem atletas europeus nas três primeiras posições?
Vamos determinar em quantas destas maneiras somente os atletas europeus preenchem o pódio. São 5 atletas para 3 posições:
A 5,3 = 5!/(5-3)! = 5!/2! = 5×4x3x2!/2! = 5×4x3 = 60
Em 60 destas maneiras só aparecem atletas europeus nas primeiras posições.
c) Em quantos resultados o atleta brasileiro recebe medalha?
Agora uma destas medalhas tem que ser do brasileiro, então restam 7 atletas para disputar 2 posições:
A 7,2 = 7!/(7-2)! = 7!/5! = 7×6x5!/5! = 7×6 = 42
Mas, como importa a ordem,o atleta brasileiro pode receber a medalha de ouro, prata ou bronze, temos 3 posições diferentes para ele, daí:
42×3 = 126 resultados em que o atleta brasileiro recebe medalha.
d) Supondo que o atleta brasileiro não recebeu medalha, determine o número de resultados em que há mais atletas europeus do que americanos no pódio?
Para termos essa situação temos dois casos:
- Um dos atletas americanos recebe uma medalha no pódio (que pode ser ouro, prata ou bronze, por isso vamos x3). Então teremos 2 posições ocupadas por atletas europeus e 1 por um americano:
06. Em uma escola está sendo realizado um torneio de futebol de salão, no qual dez times estão participando. Quantos jogos podem ser realizados entre os times participantes em turno e returno?
07. Calcule o número de arranjos simples de 10 elementos tomados 3 a 3.
08. Calcule:
a) A6,4 b )A5,3 c) A15,2 d) A4,1
a) 551 b) 552 c) 553 d) 554 e) 555
10. Com os algarismos 1, 2, 3, 4, 5, 6 e 7, quantos números de 4 algarismos distintos podemos escrever?
11.(OSEC-SP) Uma faculdade mantém 8 cursos diferentes. No vestibular, os candidatos podem fazer opção por 3 cursos, determinando-os por ordem de preferência. Então, o número de posível de formas de optar é:
a) 6.720 b) 336 c) 520 d) 120 e) 56
12) (FUVEST 2010) Maria deve criar uma senha de 4 dígitos para sua conta bancária. Nessa senha, somente os algarismos 1,2,3,4,5 podem ser usados e um mesmo algarismo pode aparecer mais de uma vez. Contudo, supersticiosa, Maria não quer que sua senha contenha o número 13, isto é, o algarismo 1 seguido imediatamente pelo algarismo 3 . De quantas maneiras distintas Maria pode escolher sua senha?
a) 551
b) 552
c) 553
d) 554
e) 555
Gabarito:
1) 665.280 2) 151. 200 3) 40 4) 12.600 5) a) 336 b) 60 c) 120 d) 2 6) 40 7) 720 8) a) 360 b) 60 c) 210 d) 4 9) A 10) 720 11) B 12) A
Olá,
Saiba quais são as principais causas da queda de cabelo e veja como evitar
esse mal que afeta homens e mulheres, sem gastar com produtos caros.
Acesse Agora: http://www.pareaquedadecabelo.com/af/5190

A 10 questão, está errada o resultado, não dá 720, e sim 840. A7,4=7/(7-4)= 7×6×5×4=840.
ResponderExcluirpois é, eu fiz a conta aqui e deu 840, eles colocaram errado a resoista
ExcluirMesmo resultado 840.
ExcluirNão da confiar nas respostas daqui
Mesmo resultado 840.
ExcluirNão da confiar nas respostas daqui
Questão 6 errada : dão 90 jogos no total - 5 jogos a cada 18 rodadas, e não 40 jogos
ResponderExcluirSeu cu q é errado
ExcluirSeu cu q é errado
ExcluirRealmente são 90 jogos na questão 6.
ResponderExcluirSendo 10 times: A,B,C,D,E,F,G,H,I e J.
O time A joga 9x ( AxB, AxC, AxD, AxE, AxF, AxG, AxH, AxI, AxJ) , já o B joga 8 visto que já jogou com o A na ida, e assim sucessivamente. Somamos 9+8+7+6+5+4+3+2+1= 45
Como é ida e volta 45x2= 90.
Nao seria 180 jogos, já q uma Aranjo 10 de 2 a 2, dá como resultado 90 jogos, 90*2 =180 turno e returno
ResponderExcluirAmigo Anônimo o resultado é 90, pois não se trata de um Arranjo e sim de uma Combinação, visto que o Jogo A x B = B x A. Mas, se você considerar Arranjo, logo encontrará o resultado já contando Ida e Volta. Abraço!
ExcluirEste comentário foi removido pelo autor.
ResponderExcluirJá que os confrontos **
ResponderExcluirSe trata de de um arranjo, já que se temos os confrontos A x B e B x A São diferentes( turno e returno). Portanto é arranjo.
ResponderExcluirA10,2 = 90
ResponderExcluir